Design method for active slope reinforcement: A case study of excavated slopes
-
摘要:目的
边坡失稳破坏具有较强的时空特征，现有被动设计方法造成大量挖方边坡工程失稳。分析边坡开挖时空演化规律，探讨边坡主动加固设计方法，对边坡信息化施工和安全控制尤为重要。
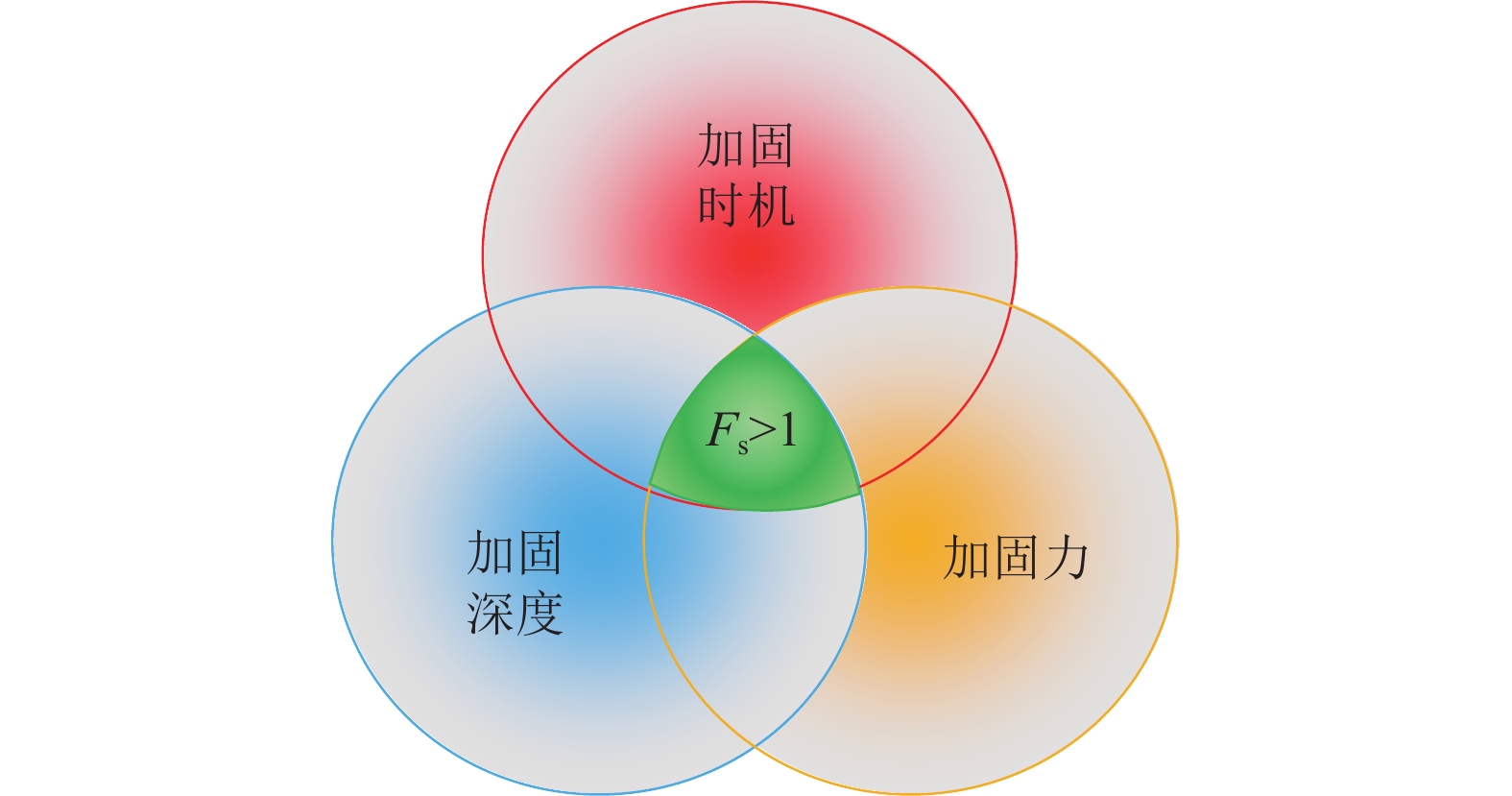
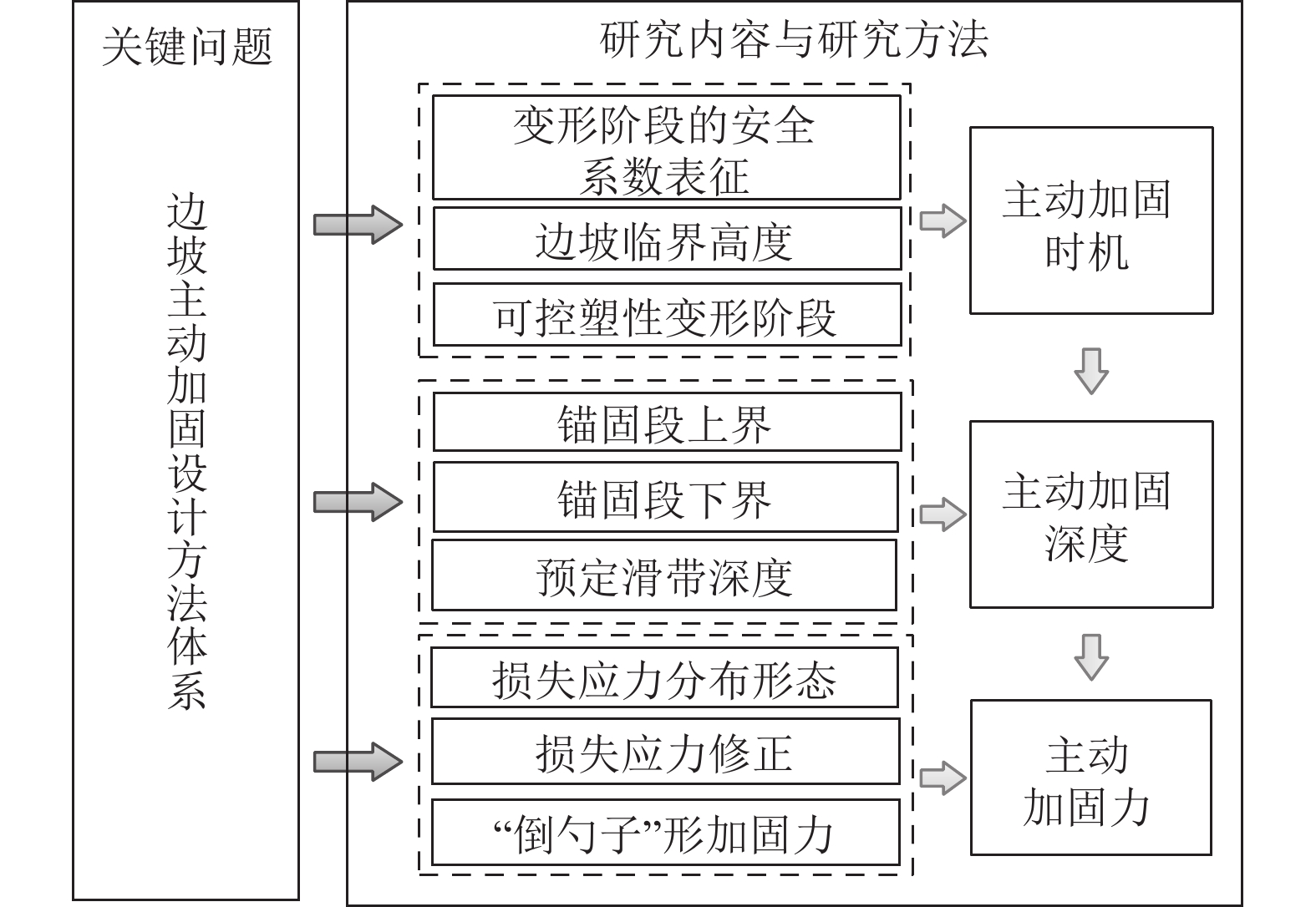
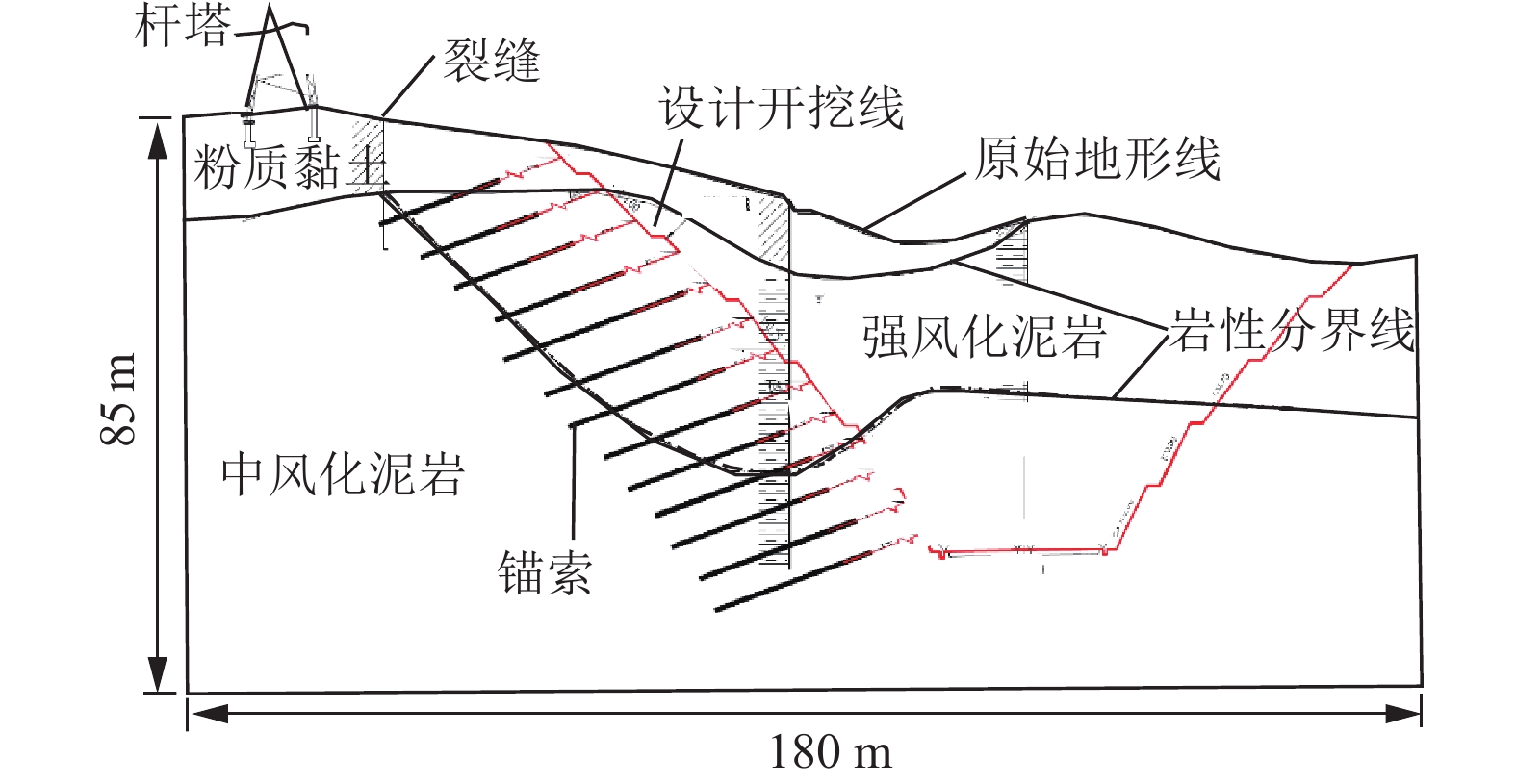
方法采用现场调研和数值模拟手段，分析高边坡开挖破坏原因和滑带主应力演化规律，揭示边坡开挖渐进破坏机制，进一步构建以加固时机、加固深度、加固力为核心三要素的边坡主动加固设计方法体系，并通过典型挖方边坡工程检验方法的可行性。
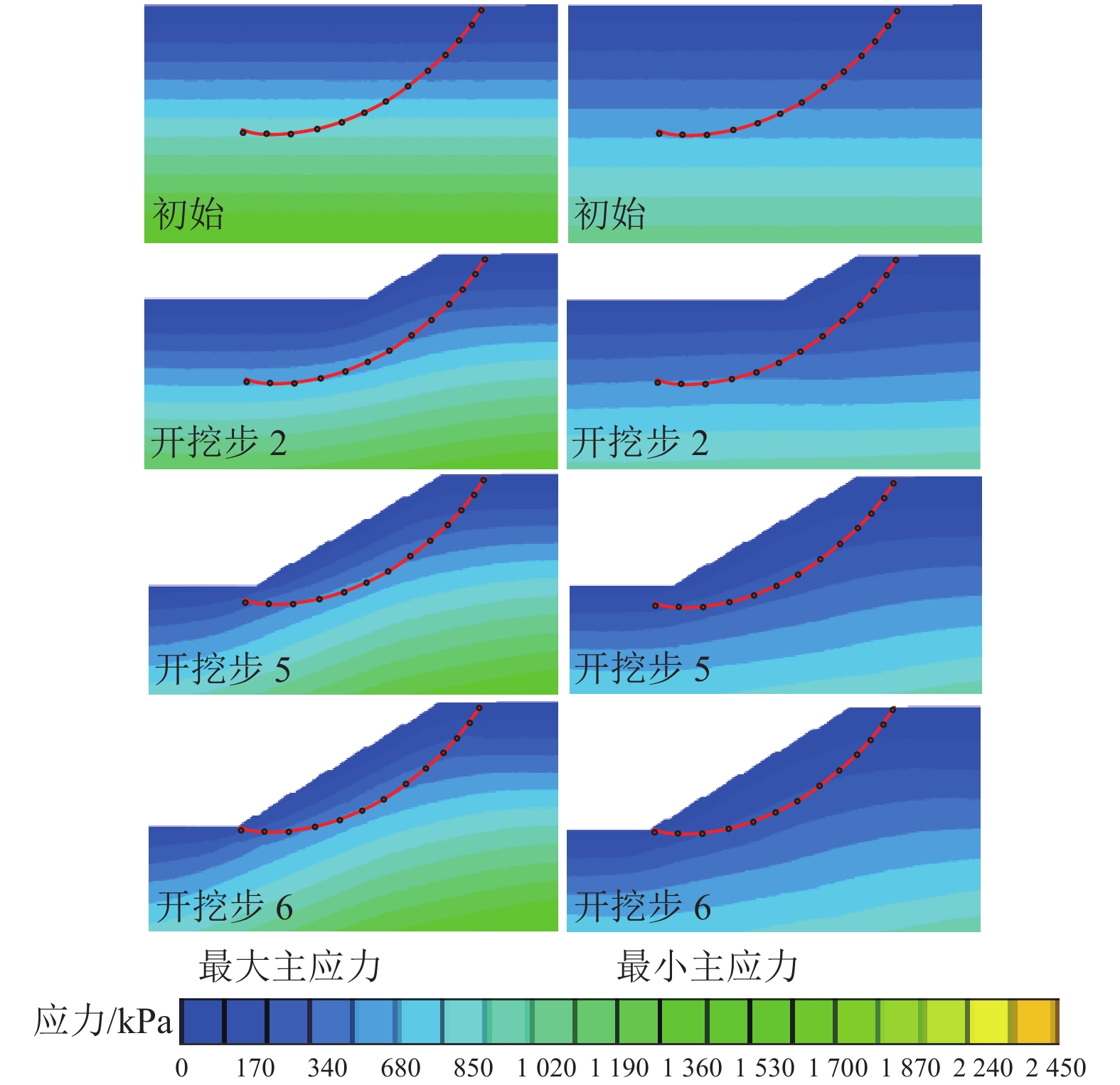
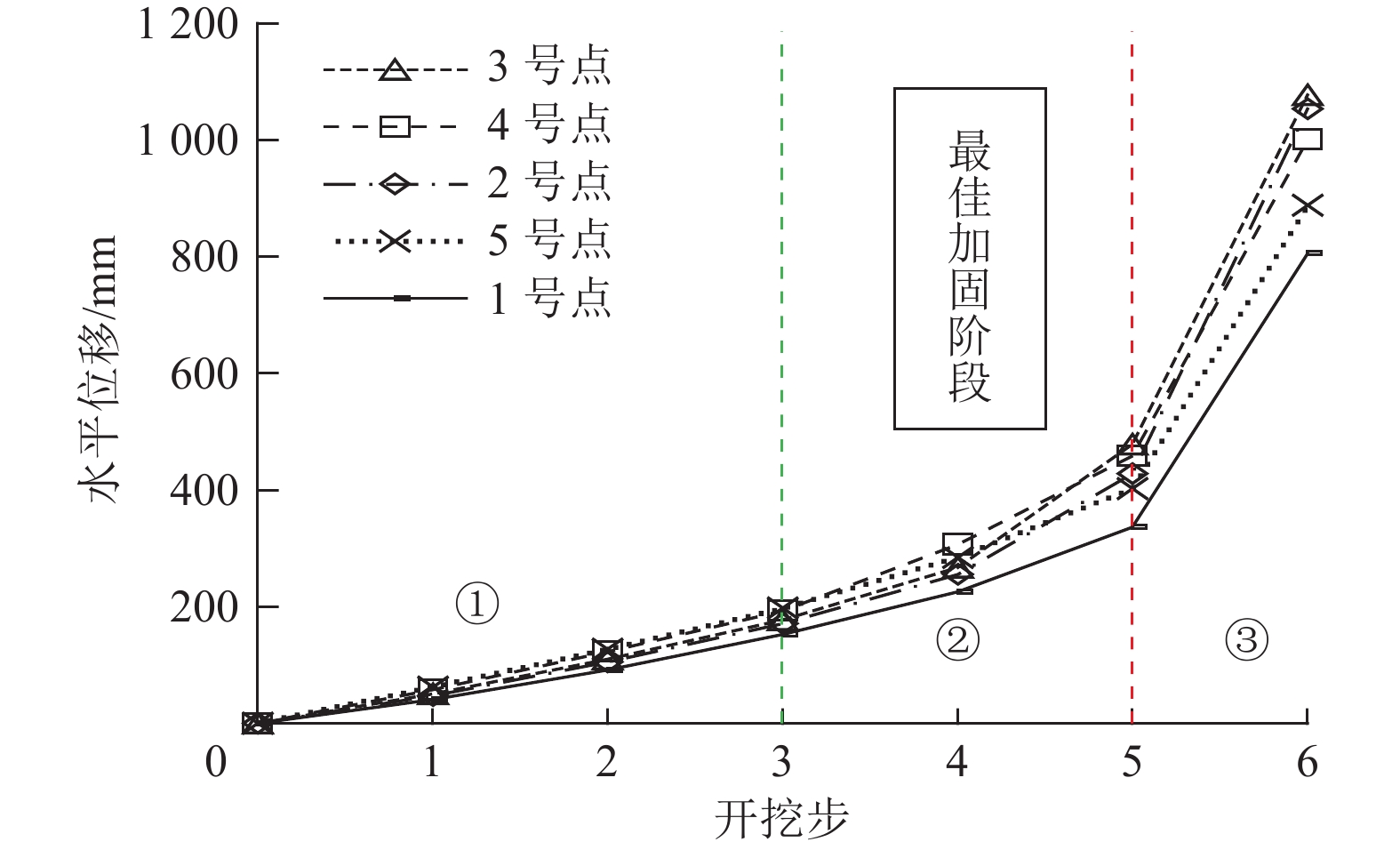
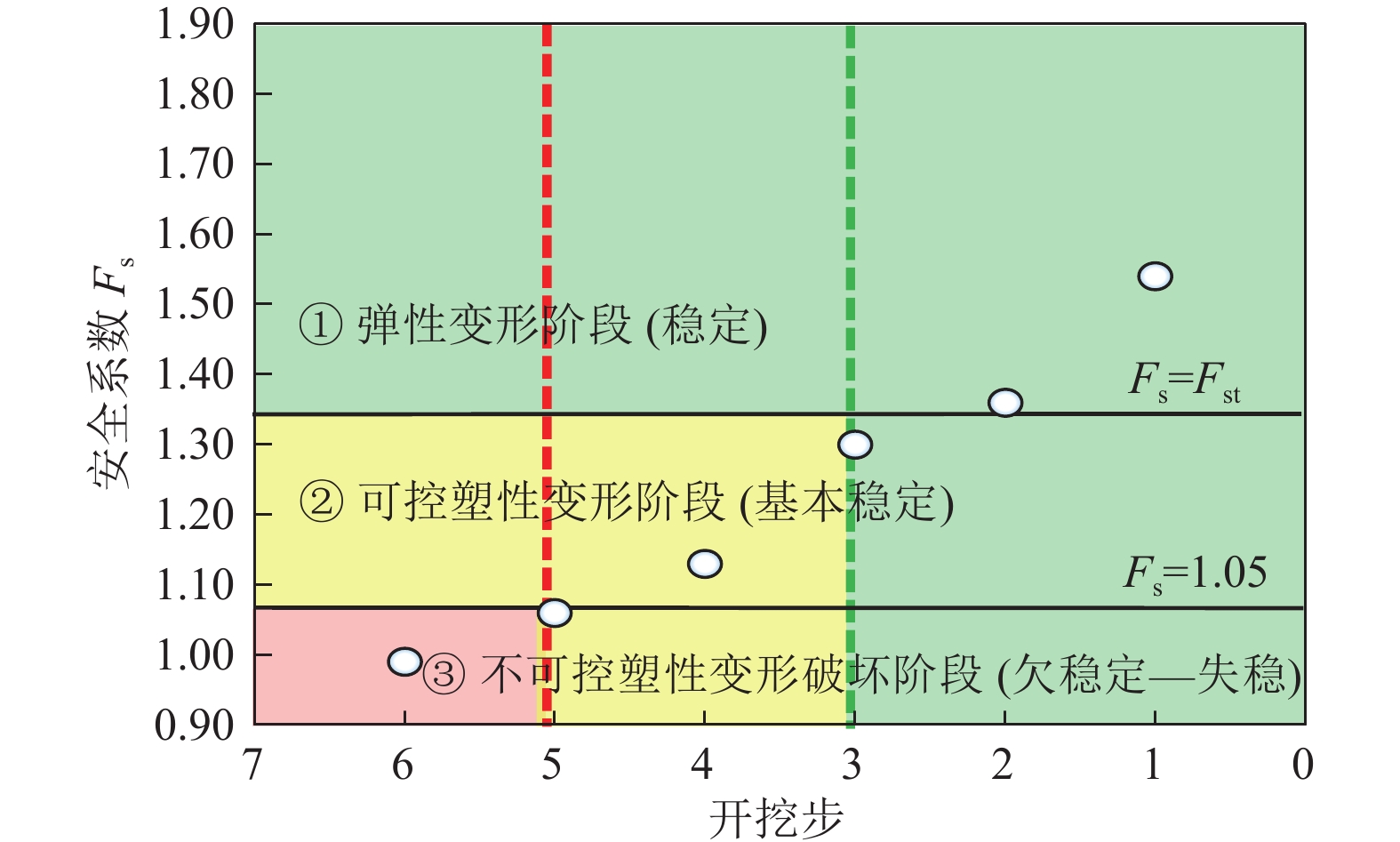
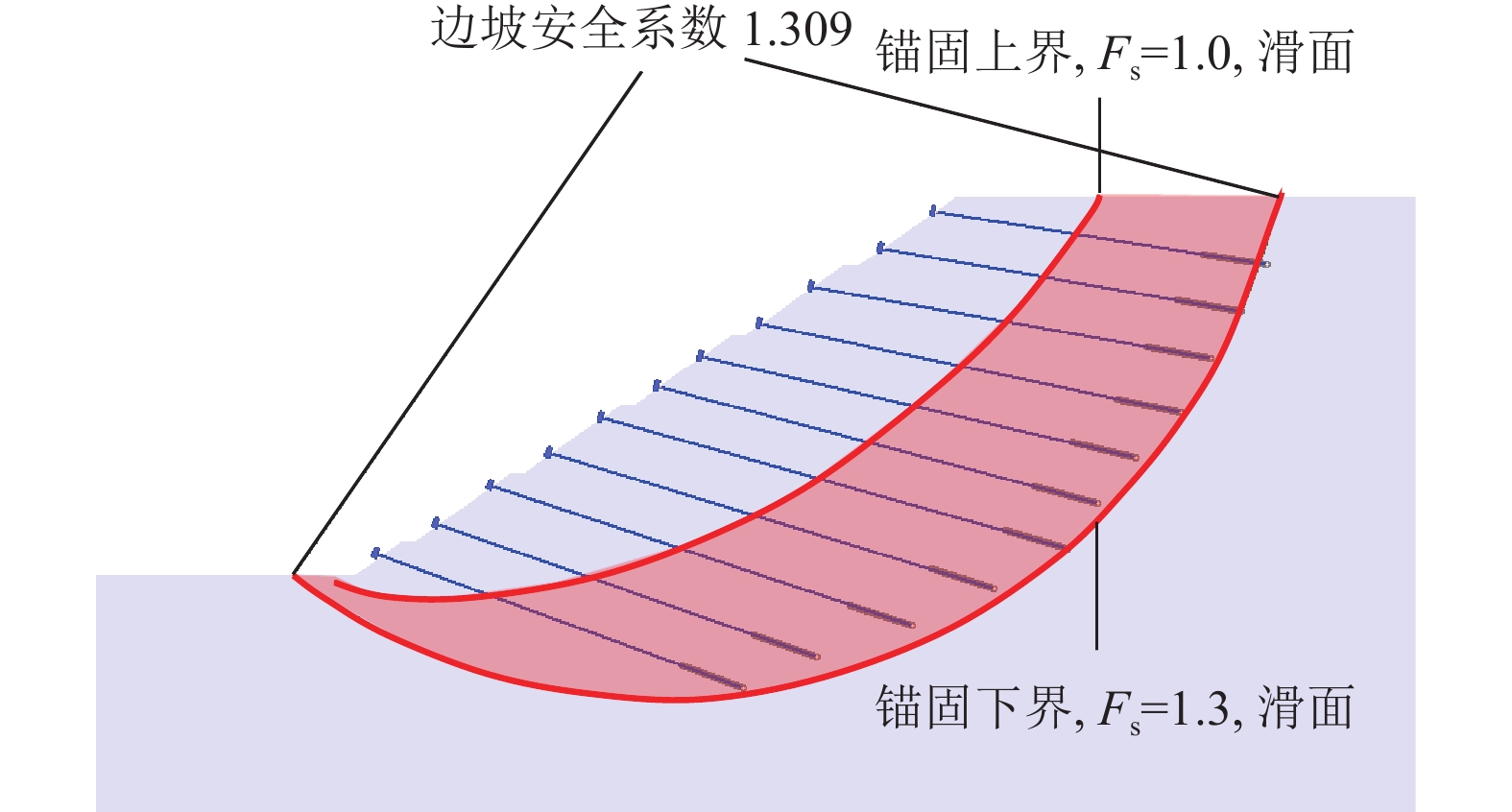
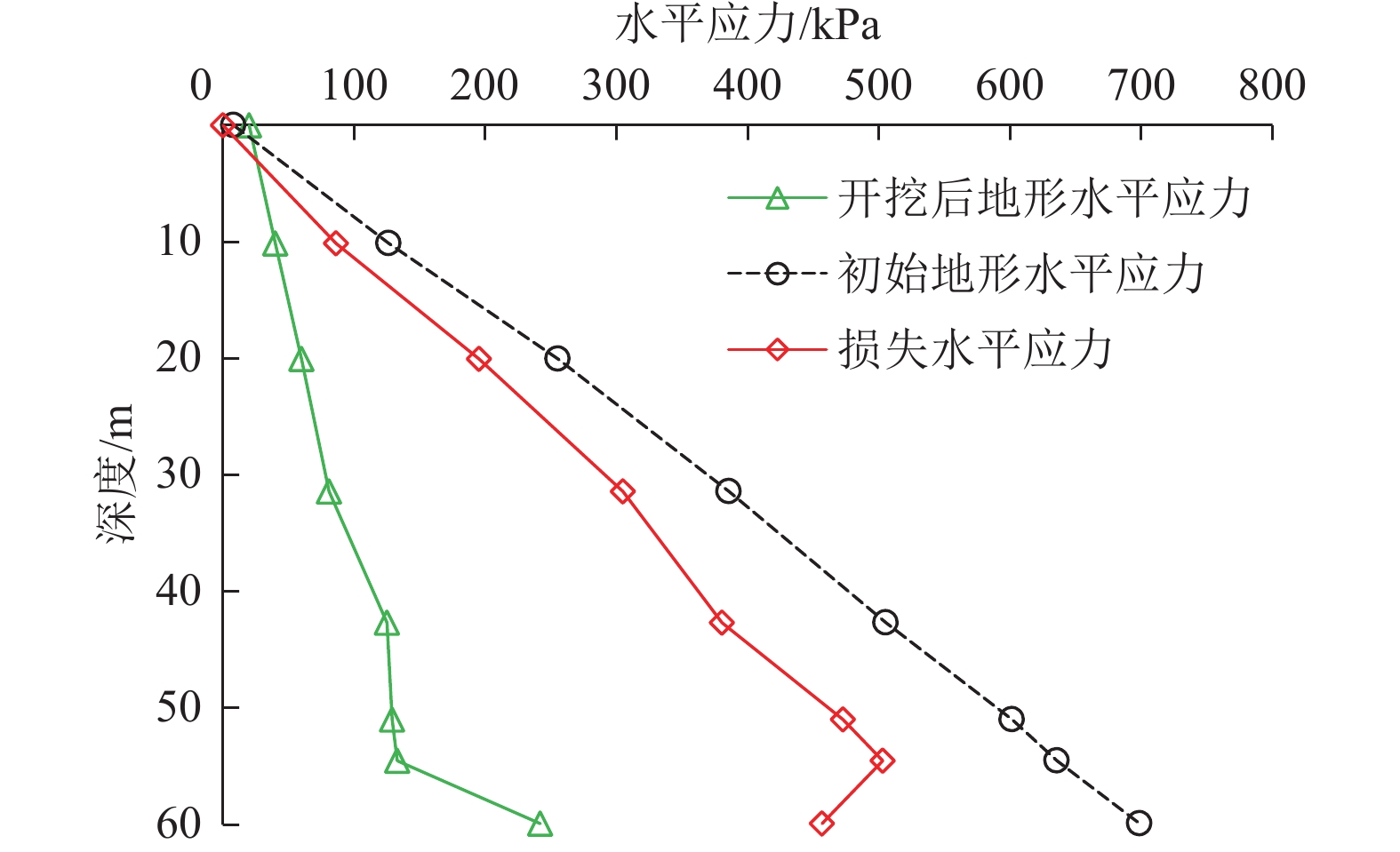
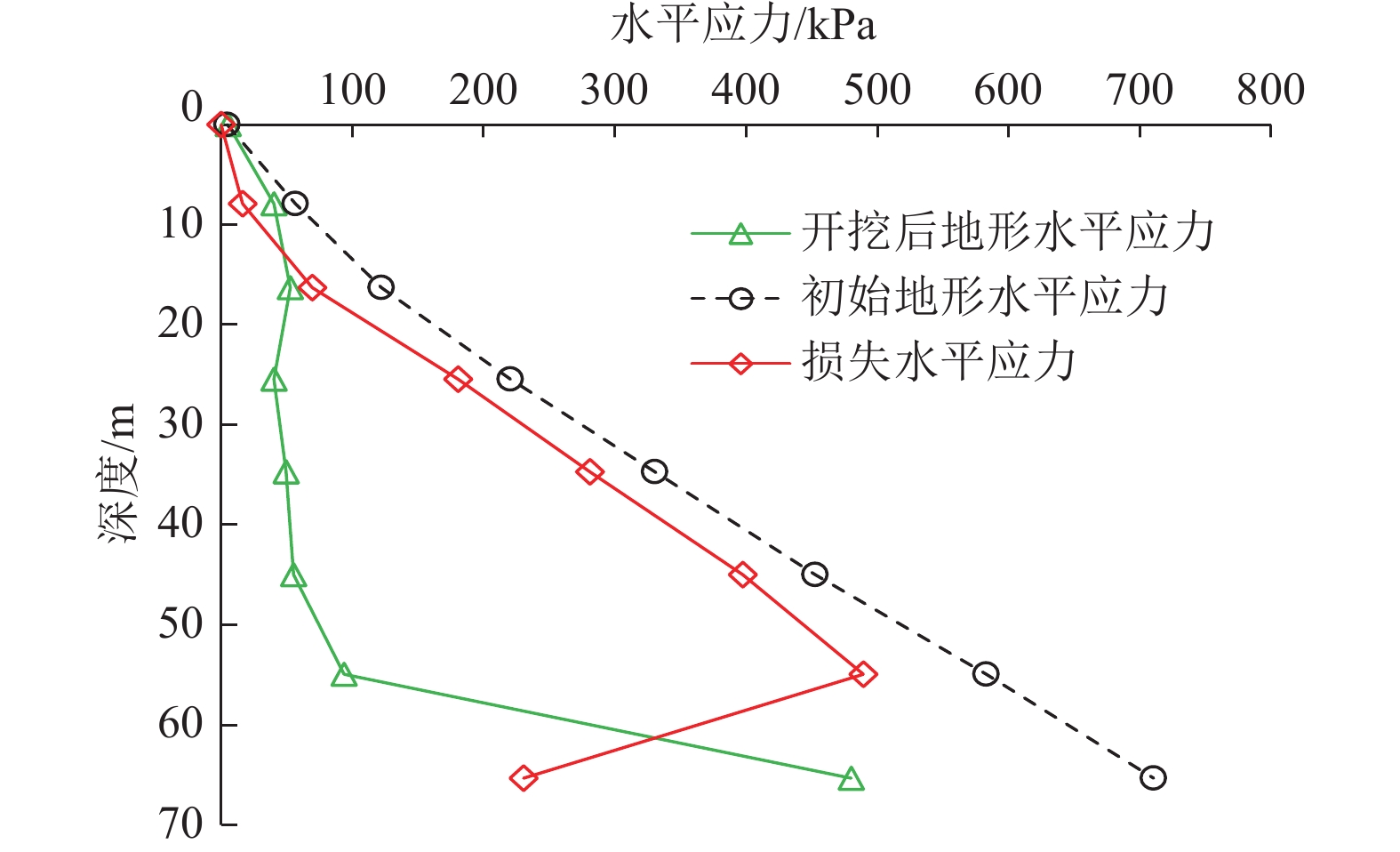
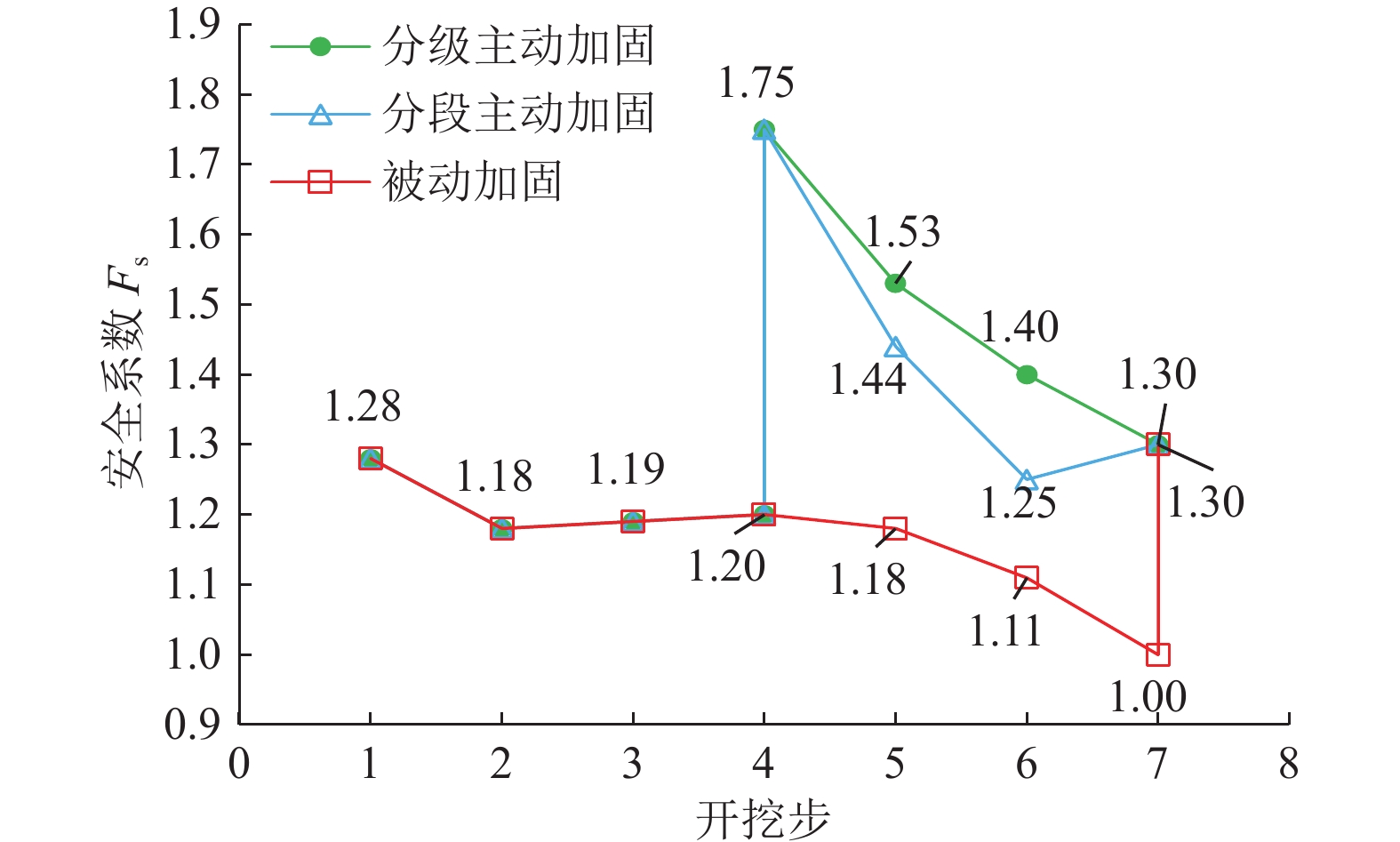
结果和结论结果表明：(1)挖方边坡开挖失稳破坏过程可划分为：破坏应力孕育期、稳定发展期和急速发展期。(2)建立挖方边坡变形阶段和安全系数(Fs)与开挖步的表征关系，可控弹塑性变形阶段1.05≤Fs≤Fst(设计安全系数)为最佳加固时机；临界坡高计算方法可以更加方便地确定加固时机，0.4 Hcr~0.7Hcr(临界坡高)为最佳加固时机。(3)提出主动加固深度上下界的界定方法，主动加固时锚固段的深度需在锚固上界之下，且达到锚固下界。(4)考虑开挖损失应力补偿，提出每级坡主动加固力的确定方法，保证开挖过程中边坡稳定性。(5)通过工程案例进行主动和被动加固设计比较，得出采用提出的主动加固设计方法只需要相对较小的加固力即可较好地约束边坡变形和塑性区扩展。研究成果可为挖方边坡工程信息化施工和加固设计提供指导。
Abstract:ObjectiveSlope instability and failure exhibit extinct spatiotemporal characteristics. Existing design methods for passive reinforcement have resulted in the engineering instability of numerous excavated slopes. Therefore, analyzing the spatiotemporal evolutionary patterns of slopes during excavation and exploring the design methods for active slope reinforcement are particularly important for the information technology (IT)-based construction and safety control of slopes.
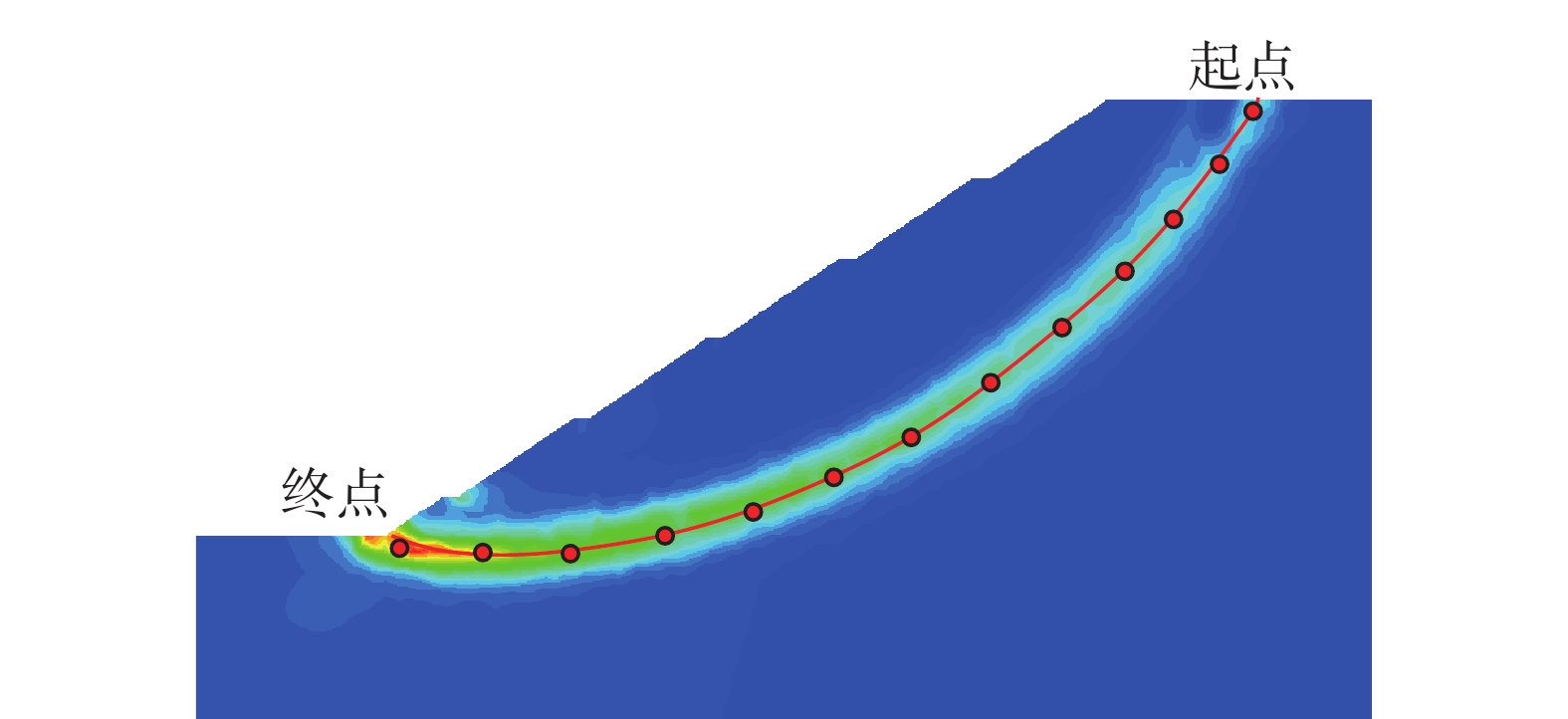
MethodsUsing on-site investigations and numerical simulations, this study analyzed the causes of excavation-induced failure of high slopes, as well as the evolutionary pattern of the principal stresses in the sliding zone. Consequently, this study revealed the progressive failure mechanism of slopes during excavation and developed a design system for active slope reinforcement with reinforcement timing, depth, and force as key factors. Finally, this study verified the feasibility of the system using typical slope excavation engineering.
Results and ConclusionsThe results indicate that the excavation-induced failure process of a slope can be divided into three periods: the incubation, stable development, and rapid development periods of failure stress. The characterization of the deformation stage and safety factor (Fs) of the excavated slope using the excavation steps was established, revealing that the optimal reinforcement timing was the time when 1.05≤Fs≤Fst (design safety factor) in the controllable elastic and plastic deformation stage. The reinforcement timing can be more conveniently determined using the calculation method for the critical slope height, which indicates that 0.4‒0.7 Hcr (critical slope height) represents the optimal reinforcement time. The method for determining the upper and lower boundaries of the active reinforcement depth indicates that the depth of the anchorage segment should be positioned below the upper boundary of the anchorage segment and extend to its lower boundary. Considering the compensation for excavation-induced stress loss, this study proposed a method for determining the active reinforcement force of each grade of a slope to ensure slope stability during excavation. The comparison of active and passive reinforcement designs for an engineering case suggests that the proposed design method for active reinforcement allows for the effective restriction of slope deformations and plastic zone expansion using a relatively small reinforcement force. The results of this study can serve as a guide for the IT-based construction and reinforcement design of slope excavation engineering.
-
-
![]()
图 1 高速公路沿线的挖方边坡破坏情况实例
Fig. 1 Examples of excavation-induced slope failure along expressways
![]()
图 5 预定滑带上应力提取点位布设
Fig. 5 Layout of stress extraction points on the predetermined sliding zone
![]()
图 6 预定滑带上最大最小主应力比变化情况
Fig. 6 Variations in the maximum and minimum principal stress ratio of the sliding zone
![]()
图 7 预定滑带上最大最小主应力云图
Fig. 7 Nephograms showing the maximum and minimum principal stresses in the sliding zone
![]()
图 8 挖方边坡开挖变形阶段特征
Fig. 8 Diagram showing the characteristics of excavation deformation stages of excavated slope
![]()
图 15 开挖前后水平应力变化情况
Fig. 15 Variations in the horizontal stress before and after excavation
![]()
图 16 不同加固方法下边坡稳定性与开挖步关系
Fig. 16 Relationship between slope stability and excavation steps under different reinforcement methods
![]()
图 17 不同加固方法的水平位移和塑性区云图
Fig. 17 Contour maps showing the horizontal displacement and plastic zones in different reinforcement methods
表 1 边坡物理力学参数
Table 1 Physical and mechanical parameters of a slope
土层 γ/(kN·m−3) E/MPa c/kPa φ/(º) υ 黏土 19 50 15 46 0.38 
下载: 导出CSV
表 2 岩土层物理力学参数
Table 2 Physical and mechanical parameters of the soil layer
岩土层 γ/
(kN·m−3)E/
MPaυ 峰值强度 残余强度 c/kPa φ/(º) c/kPa φ/(º) 粉质黏土 20 50 0.38 24 23 8 17 强风化泥岩 23 100 0.33 68 33 13 31 中风化泥岩 24 500 0.30 78 35 18 33.5
下载: 导出CSV
表 3 计算过程中各级边坡涉及的主要的力
Table 3 Primary forces involved in various slope grades in the calculation
单位：kN/m 坡级 被动加固力 分级主动加固力 分段主动加固力 剩余推力 7 200 150 150 6 400 250 250 5 650 300 300 4 800 600 600 3 900 800 900 2 1100 1000 1100 1 450 350 400 总和 4500 3450 3700 4473
下载: 导出CSV
-
[1] QIN Hui,TANG Hua,YIN Xiaotao,et al. Disturbed zone calculation and stability evaluation method of footwall slope with slip-shear failure under excavation[J]. Journal of Central South University,2024,31(2):589−601. DOI: 10.1007/s11771-023-5511-5
[2] 南宁,李鹏,苏生瑞,等. 基于宽窄平台相结合的黄土高边坡优化设计:以陕西省子长市某工业广场高边坡为例[J]. 煤田地质与勘探,2022,50(6):155−164. DOI: 10.12363/issn.1001-1986.21.10.0566 NAN Ning,LI Peng,SU Shengrui,et al. Optimization design of high loess slope based on combination of wide and narrow platform:A case study of an industrial square in Zichang City[J]. Coal Geology & Exploration,2022,50(6):155−164. DOI: 10.12363/issn.1001-1986.21.10.0566
[3] 黄润秋. 岩石高边坡发育的动力过程及其稳定性控制[J]. 岩石力学与工程学报,2008,27(8):1525−1544. DOI: 10.3321/j.issn:1000-6915.2008.08.002 HUANG Runqiu. Geodynamical process and stability control of high rock slope development[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(8):1525−1544. DOI: 10.3321/j.issn:1000-6915.2008.08.002
[4] 任东伟,李波,曾亮亮,等. 典型路堑高边坡开挖变形机制及应对措施研究[J]. 水利与建筑工程学报,2020,18(2):190−194. DOI: 10.3969/j.issn.1672-1144.2020.02.032 REN Dongwei,LI Bo,ZENG Liangliang,et al. Deformation and failure mechanism of typical high cutting slope excavation and countermeasures[J]. Journal of Water Resources and Architectural Engineering,2020,18(2):190−194. DOI: 10.3969/j.issn.1672-1144.2020.02.032
[5] 王浩,王晓东,泮俊. 超高路堑边坡治理工程案例研究Ⅰ:边坡失稳机制模拟分析[J]. 岩石力学与工程学报,2017,36(4):899−909. WANG Hao,WANG Xiaodong,PAN Jun. A case study of super-high cut slope Ⅰ:Simulation and analysis of instability mechanism of slopes[J]. Chinese Journal of Rock Mechanics and Engineering,2017,36(4):899−909.
[6] QIN Hui,YIN Xiaotao,TANG Hua,et al. Reliability analysis and geometric optimization method of cut slope in spatially variable soils with rotated anisotropy[J]. Engineering Failure Analysis,2024,158:108019. DOI: 10.1016/j.engfailanal.2024.108019
[7] CHENG Xu,TANG Hua,QIN Hui,et al. Stress field and stability calculation method for unloading slope considering the influence of terrain[J]. Bulletin of Engineering Geology and the Environment,2024,83(2):60. DOI: 10.1007/s10064-024-03557-5
[8] 宁永香,崔希民. 矿山边坡地表变形的PSO-ELM预测模型[J]. 煤田地质与勘探,2020,48(6):201−206. DOI: 10.3969/j.issn.1001-1986.2020.06.027 NING Yongxiang,CUI Ximin. PSO-ELM prediction model for surface deformation of mine slope[J]. Coal Geology & Exploration,2020,48(6):201−206. DOI: 10.3969/j.issn.1001-1986.2020.06.027
[9] 方汕澳,许强,修德皓,等. 基于斜率模型的突发型黄土滑坡失稳时间预测[J]. 水文地质工程地质,2021,48(4):169−179. FANG Shan’ao,XU Qiang,XIU Dehao,et al. A study of the predicted instability time of sudden loess landslides based on the SLO model[J]. Hydrogeology & Engineering Geology,2021,48(4):169−179.
[10] 邓铭江,蔡正银,朱洵,等. 北疆渠道膨胀土边坡破坏机制及加固措施[J]. 岩土工程学报,2020,42(增刊2):50−55. DENG Mingjiang,CAI Zhengyin,ZHU Xun,et al. Failure mechanism and reinforcement measures of shallow slopes of expansive soils in Northern Xinjiang[J]. Chinese Journal of Geotechnical Engineering,2020,42(Sup.2):50−55.
[11] 宁永香,崔希民,崔建国. 基于ABC-GRNN组合模型的露天矿边坡变形预测[J]. 煤田地质与勘探,2023,51(3):65−72. DOI: 10.12363/issn.1001-1986.22.08.0608 NING Yongxiang,CUI Ximin,CUI Jianguo. Deformation prediction of open-pit mine slope based on ABC-GRNN combined model[J]. Coal Geology & Exploration,2023,51(3):65−72. DOI: 10.12363/issn.1001-1986.22.08.0608
[12] POSTILL H,HELM P R,DIXON N,et al. Forecasting the long-term deterioration of a cut slope in high-plasticity clay using a numerical model[J]. Engineering Geology,2021,280:105912. DOI: 10.1016/j.enggeo.2020.105912
[13] KARRAY M,HUSSIEN M N,DELISLE M C,et al. Framework to assess pseudo-static approach for seismic stability of clayey slopes[J]. Canadian Geotechnical Journal,2018,55(12):1860−1876. DOI: 10.1139/cgj-2017-0383
[14] 李红卫. 陡倾顺层路堑高边坡变形破坏机制分析[J]. 岩土工程学报,2011,33(增刊1):153−158. LI Hongwei. Deformation and failure mechanism of steeply dipping bedding high slopes[J]. Chinese Journal of Geotechnical Engineering,2011,33(Sup.1):153−158.
[15] 许强. 滑坡的变形破坏行为与内在机理[J]. 工程地质学报,2012,20(2):145−151. DOI: 10.3969/j.issn.1004-9665.2012.02.001 XU Qiang. Theoretical studies on prediction of landslides using slope deformation process data[J]. Journal of Engineering Geology,2012,20(2):145−151. DOI: 10.3969/j.issn.1004-9665.2012.02.001
[16] QIN Hui,YIN Xiaotao,TANG Hua,et al. Disturbance range characterization and reinforcement design method of concealed bedding slope[J]. Engineering Failure Analysis,2024,162:108413. DOI: 10.1016/j.engfailanal.2024.108413
[17] 竺明星,卢红前,戴国亮,等. 基于双土拱效应的砂性土滑坡中抗滑排桩滑坡推力研究[J]. 湖南大学学报(自然科学版),2018,45(S0):8−13. ZHU Mingxing,LU Hongqian,DAI Guoliang,et al. Research on landslide thrust of anti-slide row piles in sandy slope with consideration of double soil-arching effects[J]. Journal of Hunan University (Natural Sciences),2018,45(S0):8−13.
[18] 李宁,钱七虎. 岩质高边坡稳定性分析与评价中的四个准则[J]. 岩石力学与工程学报,2010,29(9):1754−1759. LI Ning,QIAN Qihu. Four criteria of stability analysis and assessment of high rock slope[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(9):1754−1759.
[19] 宋桂锋,茶增云,王庆龙,等. 全强风化边坡破坏机理及加固措施研究[J]. 交通科学与工程,2020,36(2):7−15. DOI: 10.3969/j.issn.1674-599X.2020.02.002 SONG Guifeng,CHA Zengyun,WANG Qinglong,et al. Study on failure mechanism and reinforcement measure of completely weathered rock slope[J]. Journal of Transport Science and Engineering,2020,36(2):7−15. DOI: 10.3969/j.issn.1674-599X.2020.02.002
[20] 李培锋,李斯涛,李春,等. 潜在不稳定边坡复合式主动加固方法研究[J]. 施工技术,2021,50(4):95−98. LI Peifeng,LI Sitao,LI Chun,et al. Research on composite active reinforcement method for potentially unstable slope[J]. Construction Technology,2021,50(4):95−98.
[21] 董高一,周春梅,许方党,等. 含球状风化体混合花岗岩边坡稳定性及加固方案[J]. 安全与环境工程,2024,31(2):180−192. DONG Gaoyi,ZHOU Chunmei,XU Fangdang,et al. Stability and reinforcement scheme of mixed granite slope with spherical weathering body[J]. Safety and Environmental Engineering,2024,31(2):180−192.
[22] 李韬,徐奴文,戴峰,等. 白鹤滩水电站左岸坝肩开挖边坡稳定性分析[J]. 岩土力学,2018,39(2):665−674. LI Tao,XU Nuwen,DAI Feng,et al. Stability analysis of left bank abutment slope at Baihetan hydropower station subjected to excavation[J]. Rock and Soil Mechanics,2018,39(2):665−674.
[23] 陈秀清,王宝玉,魏金龙,等. 兰州徐家湾某边坡治理工程二次加固措施研究[J]. 安全与环境工程,2023,30(5):166−173. CHEN Xiuqing,WANG Baoyu,WEI Jinlong,et al. Secondary reinforcement measures of anti-slide piles in a slope treatment engineering in Xujiawan,Lanzhou[J]. Safety and Environmental Engineering,2023,30(5):166−173.
[24] 闫强. 高速公路改扩建工程高边坡开挖过程稳定性研究[D]. 西安:长安大学,2015. YAN Qiang. Study on the slope stability in the excavation process of reconstruction highway[D]. Xi’an:Chang’an University,2015.
计量
- 文章访问数: 80
- HTML全文浏览量: 9
- PDF下载量: 20
