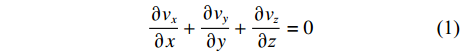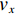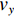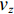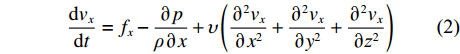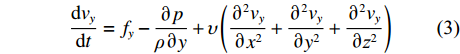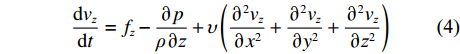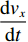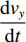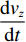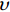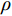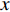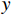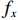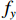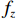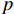Study on factors influencing the self-propelling capacity of self-propelled water jet drill bits
-
摘要:
管道内流场结构特性是影响自驱钻头自进力和解堵除垢能力的关键因素。针对多股射流共同作用下管道内流场变化影响自进力和返水阻力的问题，基于FLUENT数值分析不同条件下管道内流场变化，得到后置喷嘴角度、转速、环空比和系统压力对自进力的影响规律，揭示综合摩擦因素理论值存在误差的原因，通过正交数值模拟明确自进力影响因素的主次关系。基于自进力测试实验装置，开展不同条件下自进力测试实验，验证数值模拟结果的正确性。结果表明：涡旋挤压碰撞作用和射流卷吸作用导致自驱钻头前后产生压力梯度，从而提高自进力。后置喷嘴倾角由20°增加至45°，壁面射流逆流速度由6.2 m/s增加至14.5 m/s，涡旋碰撞挤压后压力峰值由68.47 kPa增加至80.79 kPa，导致压差力增大。提高转速能够减小一次涡旋范围，当涡旋在旋转体区域发生碰撞挤压时，旋转体所受压差力增加。提高转速、系统压力或减小环空比均会增强后置射流的封隔作用，从而提高自进力。由于理论计算返水阻力时忽略了涡旋区的影响，因此综合摩擦因数理论值需要修正。环空比、系统压力、转速和后置喷嘴倾角的极差分别为300.07、111.87、60.42、36.32，影响因素主次关系为：环空比>系统压力>转速>后置喷嘴倾角。本研究可为自驱钻头结构优化设计、提高自驱钻头的自进力提供参考。
Abstract:The structural characteristics of inner flow field in a pipeline are the key factors influencing the self-propelling capacity and descaling-unblocking capability of the self-propelled drill bit. To address the problem concerning the effect of the changes in the inner flow field of a pipeline under the joint action of multiple jets on the self-propelling force and the resistance to water backflow, the changes of inner flow field in the pipeline under different conditions were numerically analyzed based on FLUENT, and thus the influence law of the angle of rear nozzle, the rotational speed, the annular ratio and the system pressure on the self-propelling force was defined, revealing the reasons for the error of the theoretical value of the integrated friction coefficient. Besides, the primary and secondary relationships of the factors influencing the self-propelling force were clarified through orthogonal numerical simulations. Then, the self-propelling force testing experiments were carried out under different conditions with the self-propelling force test device to verify the correctness of the numerical simulation results. As shown by the results, the action of vortex squeeze collision and jet suction leads to a pressure gradient in front of and behind the self-propelled drill bits, thus increasing the self-propelling force. The angle of the rear nozzle is increased from 20° to 45°, the countercurrent velocity of wall jet is increased from 6.2 m/s to 14.5 m/s and the peak pressure after vortex collision extrusion is increased from 68.47 kPa to 80.79 kPa, resulting in an increase in differential pressure. Increasing the rotational speed could reduce the range of primary vortex, while the differential pressure applied on the rotating body increases during the collision and squeeze of vortex in the rotating body area. Increasing the rotational speed and the system pressure, or reducing the annular ratio, will increase the isolation effect of the rear jet, thus increasing the self-propelling force. The theoretical value of the integrated friction coefficient needs to be corrected as the effect of the vortex zone is ignored in the theoretical calculation of the resistance to water backflow. The extreme differences of the annular ratio, system pressure, rotational speed and angle of the rear nozzle are 300.07, 111.87, 60.42 and 36.32 respectively, and the main relationships of the influencing factors are: annular ratio > system pressure > rotational speed > angle of the rear nozzle. Generally, the research in this paper could provide a reference for the optimization design in structure and the improvement of self-propelling capacity of the self-propelled drill bits.
-
Keywords:
- gas drainage /
- borehole restoration /
- borehole blockage /
- self-propelled drill bit /
- water jet
-
我国浅部煤炭资源逐渐减少甚至枯竭，未来煤炭资源开采集中于浅部延伸至深部阶段[1-2]。随着煤炭开采深度的不断增加，煤层瓦斯压力和瓦斯含量不断增加，瓦斯抽采是预防瓦斯灾害和促进瓦斯利用的有效途径[3-4]。煤矿井下瓦斯抽采以施工钻孔抽采为主，钻孔的瓦斯抽采效果直接影响矿井瓦斯灾害的治理效果[5-6]。随着抽采时间的增加，瓦斯抽采钻孔发生塌孔、堵孔的现象显著增加，导致钻孔抽采功能部分或者完全失效，瓦斯抽采效率降低[7-9]。在石油天然气开采过程中也面临类似的难题，油管结垢降低了油气田开采量和开采效率。进入开采中后期时，油气田长时间进行聚驱、水驱、复合驱等作业，使得地面集输系统和地层等输运通道都出现一定程度的结垢现象[10]。随着开采工作持续进行，结垢量增加，可能造成管道堵塞、井下作业装置难以取出等情况，严重影响油气田的正常运作和经济效益。因此，采取有效的解堵除垢措施对解决瓦斯抽采钻孔塌孔问题、提高瓦斯抽采效率、改善油气田生产效率及提高综合开发效益具有重大意义。
自驱旋转射流技术以其无损、操作简单、无污染等优点逐渐成为一种新兴的解堵除垢技术。自驱钻头作为其执行装置，其性能优劣直接决定了自进和解堵除垢能力。合理设计的自驱钻头具有优异的射流动力特性，因而研发高性能自驱钻头是国内外学者研究的重心。20世纪40年代，国外油井开发中采用了喷嘴组合的钻头结构设计。自此，水力学在喷射式钻头上的应用开始发展。C. Landers等[11]提出了应用最为广泛的自进式多孔钻头，刘玉洲等[12]将钻头结构改进后应用于煤层气开发领域，利用自进式钻头在煤层内完成径向水平钻孔，形成新的瓦斯流动通道，提高煤层气产量。针对瓦斯抽采钻孔塌孔、堵孔问题，刘勇等[13]提出采用自进式旋转钻头修复失效钻孔的方法，其利用钻头后置喷嘴反冲力作为动力，自行至钻孔堵塞段处，前置喷嘴形成水射流对堵塞物进行破碎并将其与水混合返出孔外，实现清孔排渣、钻孔修复的目的。现场实验结果表明：进行钻孔修复后，瓦斯抽采浓度提高2.09倍，瓦斯抽采流量提高2.74倍，大大提高了瓦斯抽采效率。喷嘴的角度和布置方式影响射流速度，进而影响钻头的自进力和破岩能力。贺乐昌[14]对多孔射流钻头冲击射流流场进行研究，研究结果表明：正向喷嘴采用交错型布局方式，可以保证水力射孔孔径，减少射流能量耗散。董惠娟等[15]在此基础上建立了射流钻头内部流场模型，研究了压力、围压、喷嘴直径等因素对射流钻头破岩钻孔能力的影响，为射流钻头结构优化提供依据。郭瑞昌等[16]建立了多孔式射流钻头流场计算模型，分析了射流钻头内外不同区域的流场分布情况和局部流动特性，发现反向喷嘴较大的流线转角导致射流在流道内产生流动的分离与附壁现象，大大增加了反向喷嘴的局部阻力系数。修复理论是自驱旋转射流技术工程应用的基础。针对已有的修复理论计算长钻孔修复参数时误差较大的问题，刘勇等[17]基于变质量牛顿定律建立了钻孔修复运动方程，通过系统阻力测试实验明确综合摩擦因素k的理论值需要用系数进行修正。但综合摩擦因素理论值存在误差的原因尚不清晰。多股射流导致管道内流场发生变化，自驱钻头和高压软管受力与管道内流场结构直接相关。目前对于自驱钻头流场结构研究多针对喷头部分，缺乏多股射流共同作用下管道内流场变化影响自进力和返水阻力的研究。
笔者以管道内多股射流共同作用下流场结构特性为研究对象，通过数值模拟和实验相结合的方法揭示综合摩擦因素理论值存在误差的原因，分析后置喷嘴倾角、转速、环空比和系统压力等因素对自驱钻头自进力的影响规律，明确自进力影响因素的主次关系，以期为自驱钻头的参数优化设计提供理论依据。
1 数值模拟
1.1 几何模型
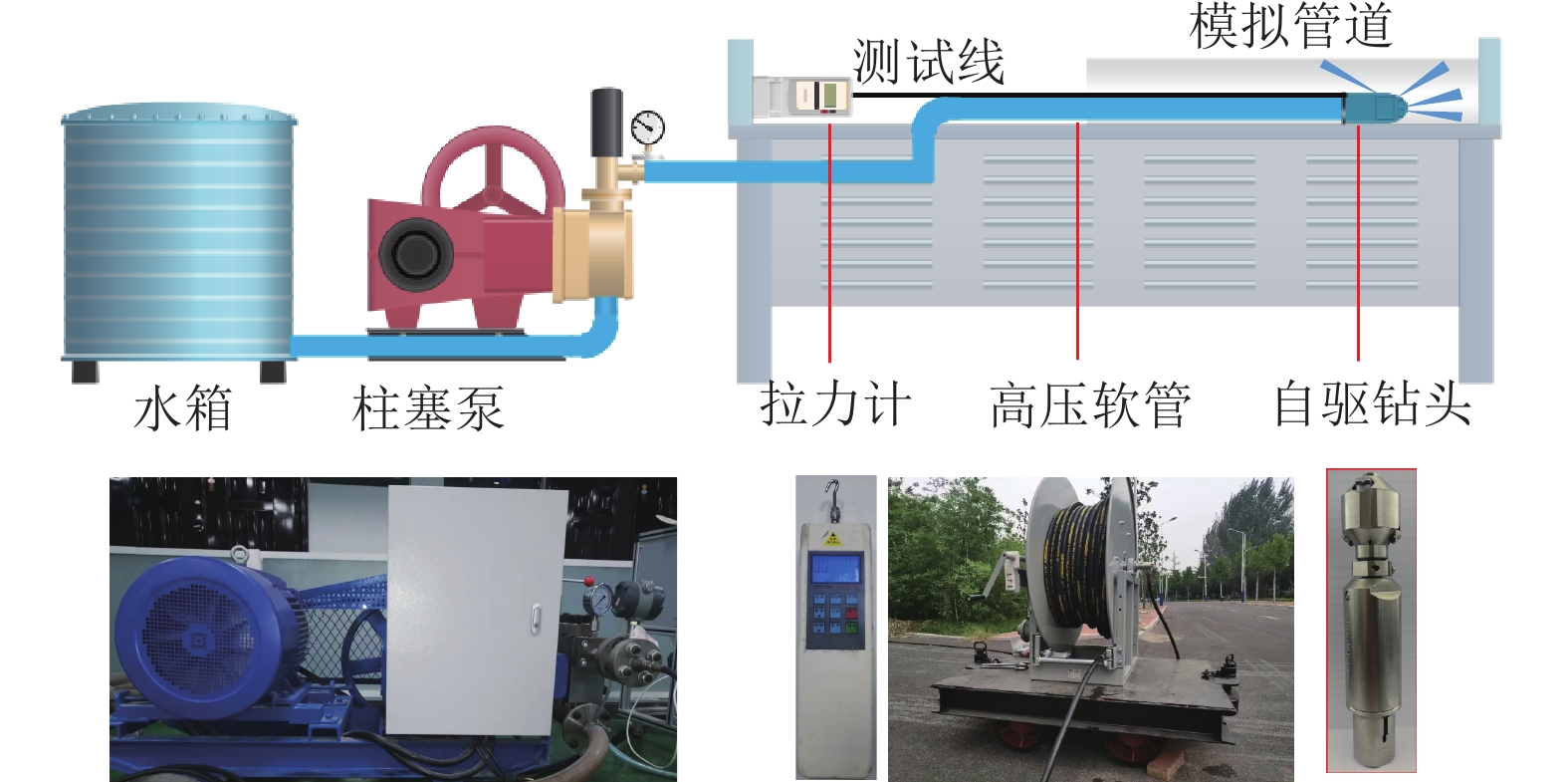
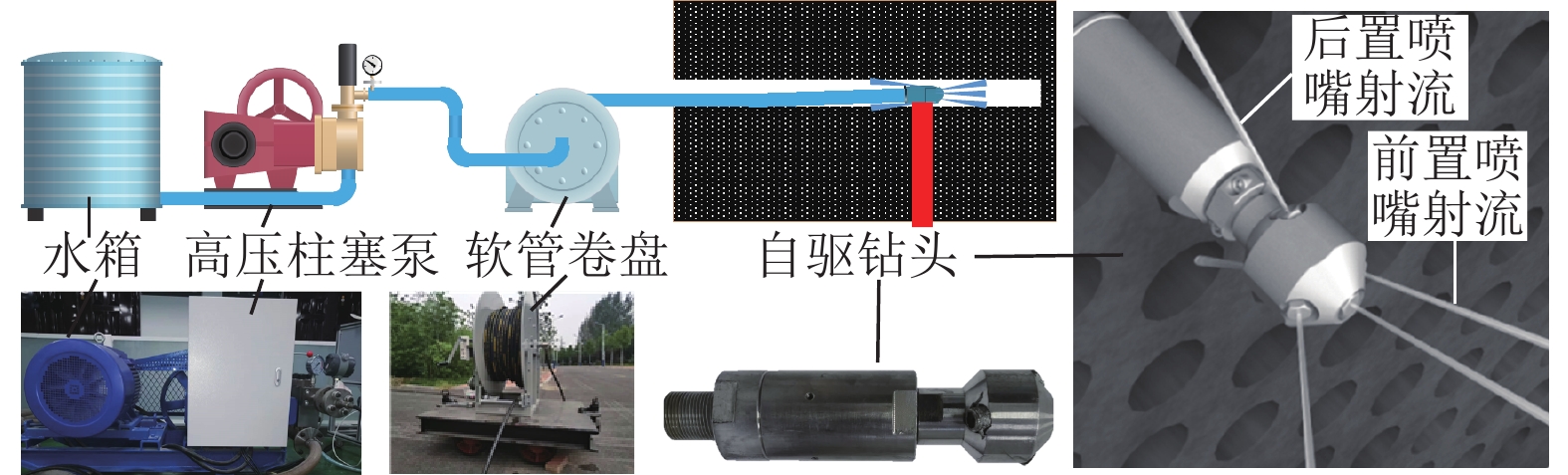
水射流自驱钻头修复钻孔装置主要由高压柱塞泵、软管卷盘和自驱钻头组成，如图1所示。自驱钻头是系统运动和破煤动力输出的关键装置。高压水射流从钻头后置喷嘴喷出，提供系统前进动力；从前置喷嘴喷出，提供破煤动力；破碎煤渣随返水排出孔外，实现钻孔修复。
![]()
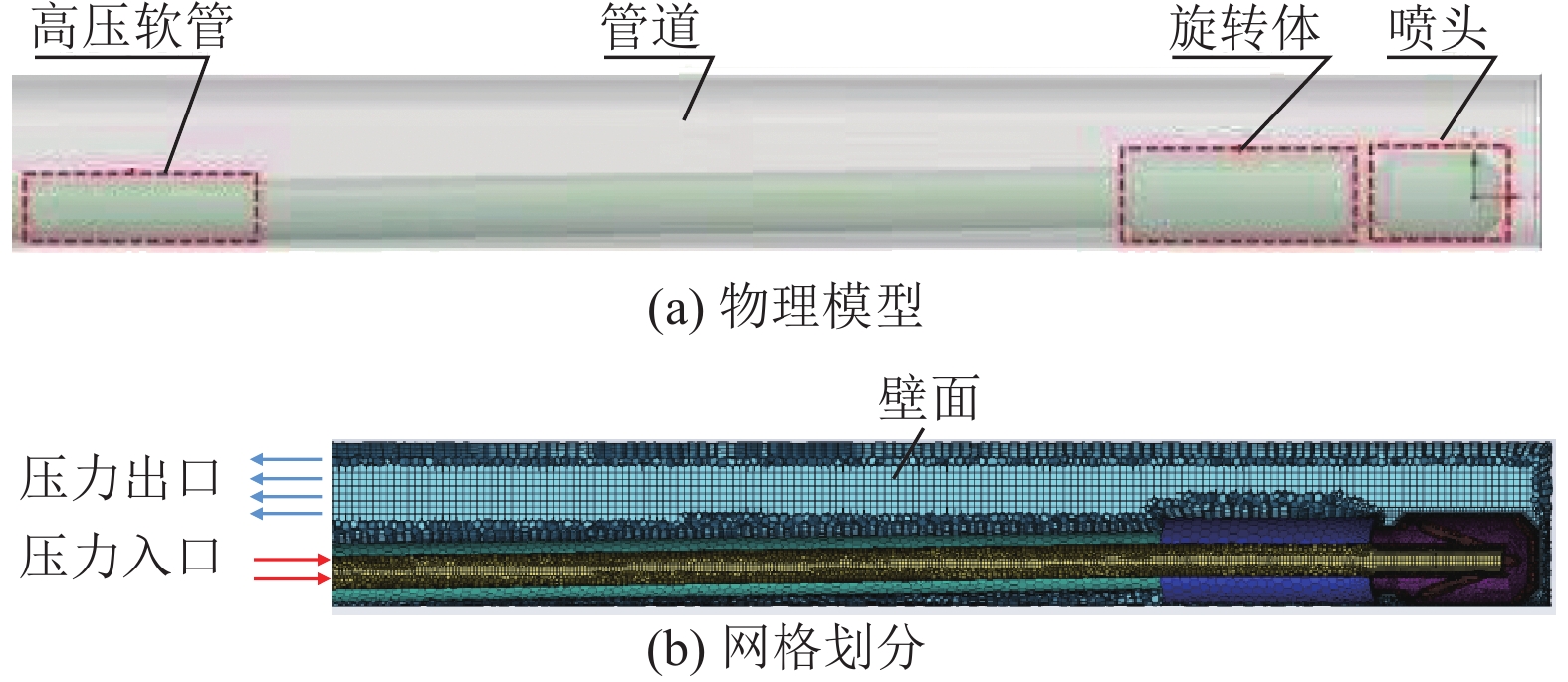
图 1 水射流自驱钻头修复钻孔装置Figure 1. Borehole restoration device of self-propelled water jet drill bit为分析管道内流场变化对自进力和返水阻力的影响规律，结合图1中高压软管与管道接触情况，利用SpaceClaim建立自驱钻头在管道中运动时的物理模型，物理模型总长度为1.1 m，如图2所示。自驱钻头由旋转体和喷头组成，总长度为158 mm，外径为40 mm，流体入口直径为16 mm，高压软管外径为28 mm。自驱钻头前端为喷头，用于安装喷嘴，流体通过高压软管进入自驱钻头，前置喷嘴射流用于解堵除垢，后置喷嘴射流用于提供推力和旋转转矩。钻头前端为3个直径1 mm喷嘴，与钻头中轴线夹角分别为35°、30°、10°，后置喷嘴直径为1.5 mm。
1.2 控制方程
水为不可压缩流体，自驱钻头运动过程中，流体与管道之间的传热对流场的影响可以忽略不计。因此，进行管道内流场数值模拟时，不考虑传热，基本控制方程包括连续方程、Navier-Stokes方程。
不可压缩流体连续方程表达式[18]为：
$$ \frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_y}}}{{\partial y}} + \frac{{\partial {v_{\textit{z}}}}}{{\partial {\textit{z}}}} = 0 $$ (1) 式中：
${{{v}}_x}$ 、${{{v}}_y}$ 、${{{v}}_{\textit{z}}}$ 分别为流体在x、y、z方向上的速度。对于不可压缩黏性流体Navier-Stokes方程，在空间直角坐标系中的表达式[18]为：
$$ \frac{{{\rm{d}}{v_x}}}{{{\rm{d}}t}} = {f_x} - \frac{{\partial p}}{{\rho \partial x}} + \upsilon \left( {\frac{{{\partial ^2}{v_x}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{v_x}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{v_x}}}{{\partial {{\textit{z}}^2}}}} \right) $$ (2) $$ \frac{{{\rm{d}}{v_y}}}{{{\rm{d}}t}} = {f_y} -\frac{{\partial p}}{{\rho\partial y}} + \upsilon \left( {\frac{{{\partial ^2}{v_y}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{v_y}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{v_y}}}{{\partial {{\textit{z}}^2}}}} \right) $$ (3) $$ \frac{{{\rm{d}}{v_{\textit{z}}}}}{{{\rm{d}}t}} = {f_{\textit{z}}} - \frac{{\partial p}}{{\rho\partial {\textit{z}}}} + \upsilon \left( {\frac{{{\partial ^2}{v_{\textit{z}}}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{v_{\textit{z}}}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{v_{\textit{z}}}}}{{\partial {{\textit{z}}^2}}}} \right) $$ (4) 式中：
$\dfrac{{{\rm{d}}{v_x}}}{{{\rm{d}}t}}$ 、$\dfrac{{{\rm{d}}{v_y}}}{{{\rm{d}}t}}$ 、$\dfrac{{{\rm{d}}{v_{\textit{z}}}}}{{{\rm{d}}t}}$ 分别为流体在x、y、z方向上的加速度；$\upsilon $ 为运动黏度；$\rho $ 为流体密度；$x$ 、$y$ 、$\textit{z}$ 分别为流体质点在$t$ 时刻的空间坐标；${f_x}$ 、${f_y}$ 、${f_z}$ 为体积力在x、y、z方向上的分量；$p$ 为压力。1.3 湍流模型
自驱钻头后置射流与钻头内部流体流动方向相反，存在较大的流线转角，导致后置喷嘴入口处局部流线严重弯曲，并且射流速度较高，诱导流场内产生涡旋。采用标准k-ε湍流模型进行管道内流场数值模拟会产生较大的误差。因此，本文采用RNG k-ε湍流模型进行数值模拟。与标准k-ε湍流模型相比，RNG k-ε湍流模型中的ε传输方程中多了一个R项，使RNG k-ε湍流模型能更加精确地模拟大应变和大流线弯曲度的流体流动问题[19]。
1.4 网格划分及边界条件
管道内部流场结构相对复杂，所以采用Fluent Meshing进行网格划分，并在壁面划分边界层网格，如图2所示。分别对流体模型的不同部分划分网格，网格最小边长为0.2 mm，网格总数为910 217，在喷嘴出口等流场变化剧烈的地方采用0.2 mm网格进行划分。模拟过程中喷头以不同转速进行旋转，因此对喷头部分进行局部加密来保证模拟效果。
边界条件设置如图2所示，包括入口、出口、壁面以及充满水的流动区域。钻头流体入口边界条件设置为压力入口，根据实际工况条件确定计算压力值，出口设置为压力出口，出口压力为大气压，壁面设置为无滑移的固定壁面。
1.5 数值模拟方案
后置喷嘴倾角、转速、环空比(管道内径为D1，高压软管外径为D2，(D1−D2)/D1定义为环空比)和系统压力影响管道内的流场结构，从而影响自驱钻头自进力。依次改变后置喷嘴倾角、转速、环空比、系统压力，其他条件不变，进行多因素逐项数值模拟，数值模拟方案见表1。
表 1 多因素逐项数值模拟方案Table 1. Scheme of multi-factor numerical simulation by item编号 后置喷嘴倾角/(°) 转速/(r·min−1) 环空比 压力/MPa 1 20 600 0.63 25 2 25 600 0.63 25 3 30 600 0.63 25 4 35 600 0.63 25 5 40 600 0.63 25 6 45 600 0.63 25 7 20 0 0.63 25 8 20 300 0.63 25 9 20 900 0.63 25 10 20 1200 0.63 25 11 20 900 0.44 25 12 20 900 0.53 25 13 20 900 0.69 25 14 20 900 0.75 25 15 20 900 0.53 10 16 20 900 0.53 15 17 20 900 0.53 20 选用自进力大小作为指标评价自驱钻头性能优劣，根据多因素逐项数值模拟结果，由自进力影响因素的全部水平组合中，选取部分有代表性的水平组合：系统压力15、20、25 MPa，后置喷嘴倾角20°、25°、35°，转速600、900、1 200 r/min，环空比0.44、0.53、0.63。根据上述水平组合，正交数值模拟4个因素的水平见表2，正交数值模拟方案见表3。
表 2 正交数值模拟因素水平Table 2. Factors and levels of orthogonal numerical simulation水平 系统压力/MPa 后置喷嘴倾角/(°) 转速/(r·min−1) 环空比 1 15 20 600 0.44 2 20 25 900 0.53 3 25 35 1 200 0.63 表 3 正交数值模拟方案Table 3. Orthogonal numerical simulation scheme编号 系统压力/MPa 后置喷嘴倾角/(°) 转速/(r·min−1) 环空比 1 15 20 600 0.44 2 15 25 900 0.53 3 15 35 1 200 0.63 4 20 20 900 0.63 5 20 25 1 200 0.44 6 20 35 600 0.53 7 25 20 1 200 0.53 8 25 25 600 0.63 9 25 35 900 0.44 2 模拟结果与分析
2.1 流场基本结构特性
图3为管道内基本流场分布情况。根据流场分布，可分为前置射流区、后置射流区、涡旋区、返流区4个区域。前置射流为3个角度不同的射流组成的射流束，后置射流区由2个射流组成。前置射流和后置射流冲击壁面会形成一次涡旋，诱导周围流体进入涡旋，没有卷入一次涡旋的流体撞击壁面后分离形成二次涡旋。涡旋的形成导致钻孔内产生复杂的涡旋区。当涡旋能量不足以诱导流体产生新的涡旋时，钻孔内流场趋于稳定，形成返流区。
2.2 多因素逐项数值模拟结果与分析
2.2.1 后置喷嘴倾角的影响
自驱钻头多股高速射流快速喷射，产生反冲力的同时在钻头区域产生局部低压区，由于压力梯度作用，使自驱钻头产生压差力。反冲力和压差力是自驱钻头实现自进的主要动力。后置喷嘴倾角在一定程度上决定着自驱钻头的自进力。因此，选择合适的后置喷嘴倾角对提高自驱钻头的自进力有积极的作用。
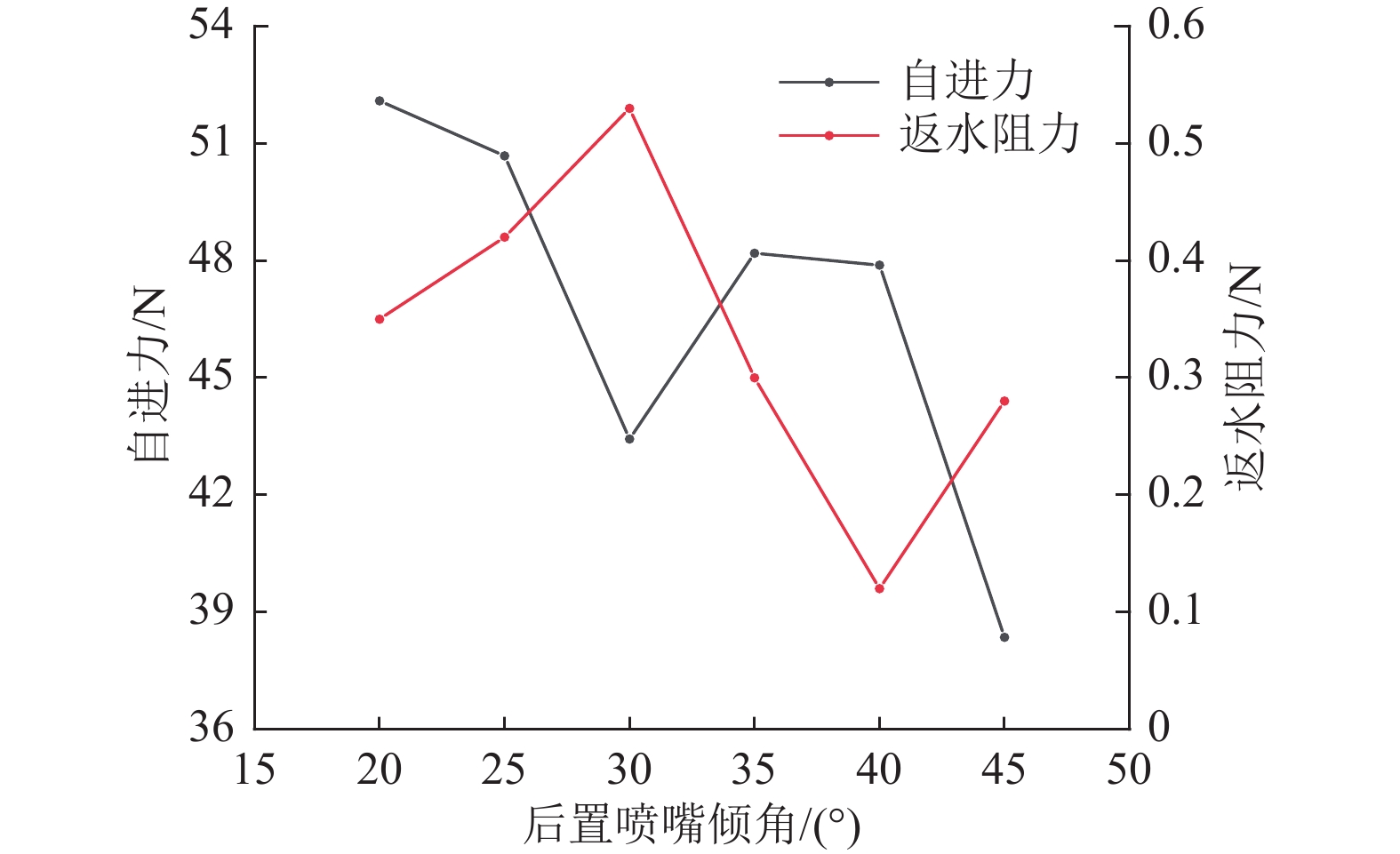
前置喷嘴的个数、直径和倾角不变，并固定后置喷嘴个数和直径。入口压力为25 MPa，环空比为0.63，后置喷嘴倾角分别为20°、25°、30°、35°、40°、45°，自进力和返水阻力变化情况如图4所示。由图4可知，随着后置喷嘴倾角由20°增加至45°，自进力逐渐减小，但后置喷嘴倾角为30°时自进力小于其他条件下自进力。
![]()
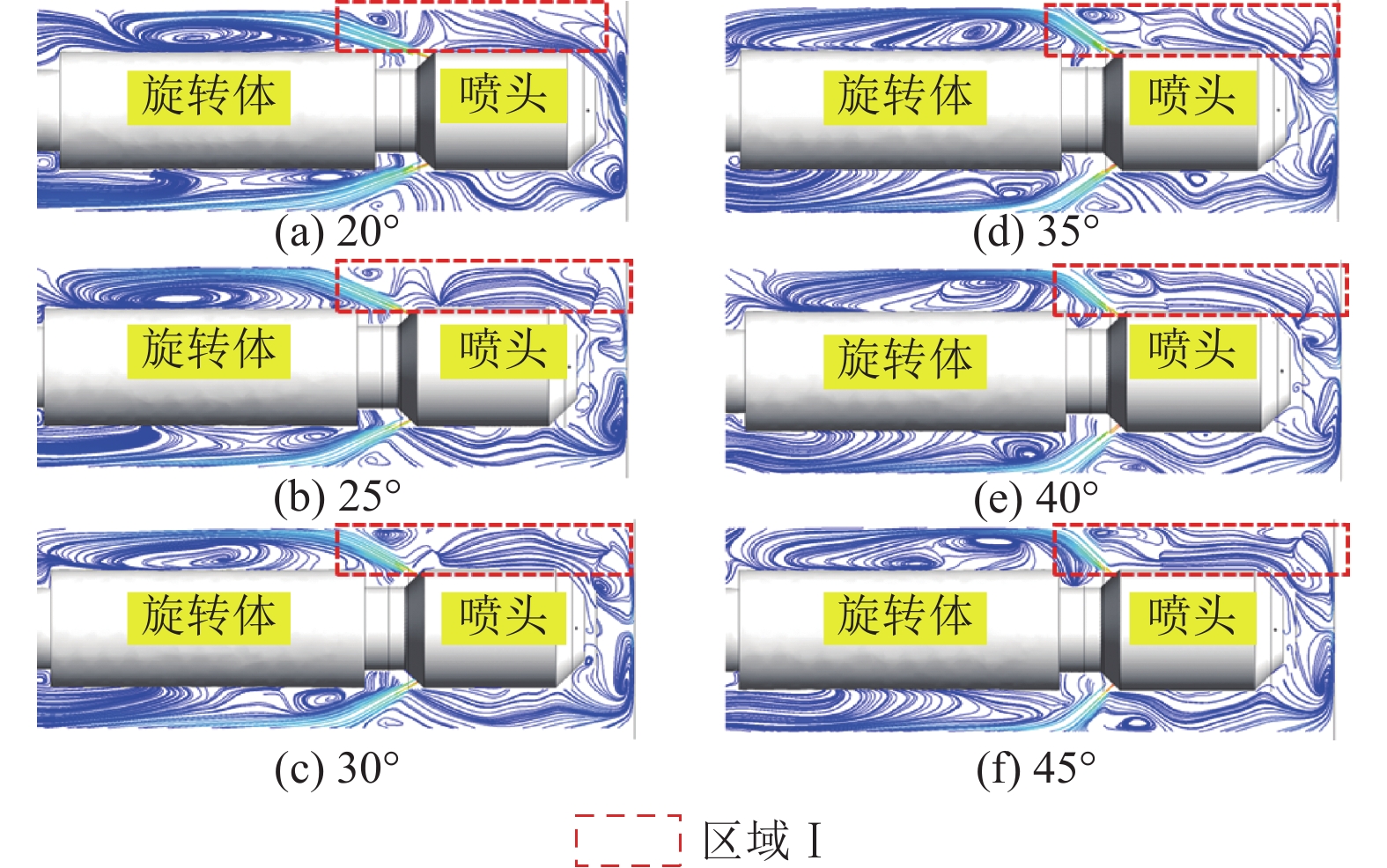
图 4 不同后置喷嘴倾角自进力和返水阻力变化Figure 4. Change of self-propelling force and resistance to water backflow at different angles of rear nozzle自驱钻头多股射流冲击壁面后速度迅速衰减，并开始沿壁面横向发展，从而形成壁面射流区，其主要由顺流(管道出口方向)区域和逆流(管道底部方向)区域组成。低速返流受到高速射流的卷吸作用以及管道内壁与喷嘴之间有限空间的限制，产生尺度不一的涡旋，涡旋不断进行分裂、变形、卷吸和合并，形成大小不一的涡旋并随机运动[20]，如图5所示。
![]()
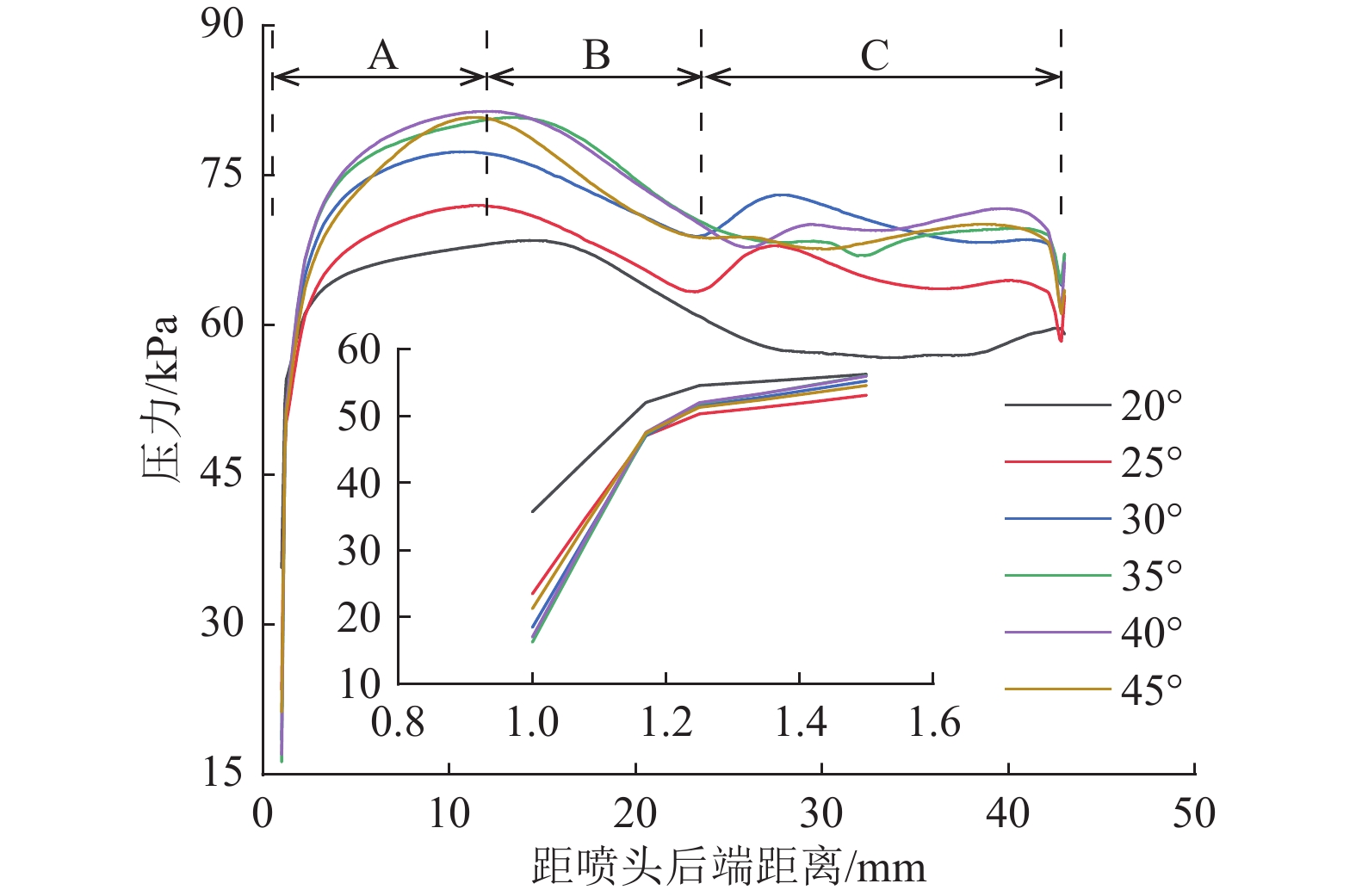
图 5 不同后置喷嘴倾角流线对比Figure 5. Comparison of streamlines at different angles of rear nozzle涡旋的发展和射流的卷吸作用影响自驱钻头前后压力梯度，从而影响压差力。图6为不同后置喷嘴倾角条件下喷头后端至前端42 mm范围内压力变化，从喷头后端至前端，压力先增大后减小。后置喷嘴高速射流喷射过程中，射流周围形成低压区，喷头后端压力较低。射流冲击壁面后，在射流两侧形成大小不一的涡旋。由图5区域Ⅰ可知，前置射流形成的涡旋与后置射流形成的涡旋发生碰撞，涡旋碰撞时对流体的挤压作用导致压力升高(图6，A阶段)。前后涡旋发生碰撞后，流体向喷头两侧流动，在前置射流的卷吸作用下，喷头前端压力降低(图6，B阶段)。由于涡旋结构交替形成、发展，喷头两侧涡旋结构不一致，导致压力出现波动(图6，C阶段)。后置喷嘴倾角小于30°时，壁面射流以顺流为主，随着后置喷嘴角度增加，逆流速度增加，射流右侧涡旋速度增大，涡旋碰撞后压力峰值随之增加。由图6可知，随着后置喷嘴倾角增加，喷头前后压力梯度增加，导致压差力增大。自驱钻头自进力主要由轴向射流反冲力和压差力组成，当后置喷嘴倾角大于30°时，压差力大于因后置喷嘴倾角增加而减小的轴向射流反冲力。因此，后置喷嘴倾角30°时自进力小于其他后置喷嘴倾角条件下自进力。
![]()
图 6 不同后置喷嘴倾角条件下喷头上方环空压力对比Figure 6. Comparison of annular pressure above nozzle at different angles of rear nozzle流体从高压软管与钻孔壁之间的环空返回时，在高压软管近壁区存在速度梯度很大的流动，产生流体对壁面的切应力，对高压软管的运动产生返水阻力[17]。根据文献[17]的研究，返水阻力是综合摩擦因素的重要组成部分，采用出口处流速代替返流速度计算返水阻力导致综合摩擦因素理论值出现误差。射流冲击壁面后，水流被限制在管道和自驱钻头之间的环形空间流动，产生水流拖曳力。水流拖曳力的方向与流体流动方向一致。由图4可知，入口压力一定时，后置喷嘴倾角影响返水阻力的大小。后置喷嘴倾角发生改变时涡旋区随之改变(图5)。涡旋区导致流体流动方向发生改变，从而影响返水阻力。采用出口处流速代替返水速度计算返水阻力时未考虑涡旋区的影响，因此综合摩擦因素理论值需要用系数进行修正。
2.2.2 转速的影响
转速是影响射流速度和涡旋范围的重要参数。设置系统压力为25 MPa，转速分别为0、300、600、900、1 200 r/min，对管道内流场进行数值模拟。后置射流旋转冲击过程中产生封隔作用，阻碍钻头后方流体回流至低压区域。环空比一定时，射流旋转速度越大，封隔作用越强。同时，射流处于旋转状态时，射流流动特征会发生偏转。同一压力条件下，旋转速度不同，射流受旋转的影响程度也不同，从而导致不同的流动规律。图7为后置喷嘴射流轴心位置速度变化，随着旋转速度增加，射流速度衰减程度加剧。
![]()
图 7 不同转速条件下射流轴心位置速度变化Figure 7. Change of velocity of jet at the axis position at different rotational speeds射流的旋转会强化射流与周围流体的掺混作用，加速射流能量的消耗和速度的衰减，从而影响涡旋结构和范围[21]。如图8所示，随着喷头旋转速度的增加，射流冲击壁面形成的壁面射流区速度降低，导致后置射流诱导形成的一次涡旋范围逐渐减小。一次涡旋(标记为D)形成过程中诱导周围流体进入，没有卷入一次涡旋的流体撞击壁面后分离形成二次涡旋(标记为E)。涡旋速度与环空直径成反比，旋转体上方涡旋速度大于高压软管上方涡旋速度。如图8所示，旋转速度为900 r/min和1 200 r/min时，一次涡旋与二次涡旋在旋转体上方发生碰撞挤压，导致压力梯度增加。在射流封隔作用和涡旋碰撞挤压作用下，自驱钻头前后压力梯度增加。转速增加有利于钻头自进，但过高的转速会加剧射流速度衰减，不利于破碎堵塞物。因此，设计自驱钻头时应考虑转速对射流速度衰减的影响，提高自进力和解堵效率。
2.2.3 环空比的影响
图9为系统压力25 MPa、后置喷嘴倾角为20°时环空比对自进力的影响规律，环空比从0.44增加至0.75，自驱钻头的自进力逐渐下降。从数值模拟结果(图10)可以看出，自驱钻头外径固定时，环空比越小，钻头前后压力梯度越大。射流冲击壁面过程中卷吸流体，产生尺度不一的涡旋，在管道底部形成低压区域。后置射流旋转冲击过程中产生封隔作用，阻碍钻头后方流体回流至低压区域。系统压力一定时，后置射流的封隔能力有限，当环空比超过后置射流的封隔范围时，钻头后方流体对被射流卷吸的流体进行补充，从而导致钻头前后压力梯度减小。入口压力和后置喷嘴倾角不变的情况下，环空比为0.44时，自驱钻头和管道间环空直径较小，后置射流的封隔作用较强，阻碍流体回流，导致射流卷吸的流体无法得到补充，自驱钻头前后压力梯度较大。随着环空比增大，后置射流封隔作用逐渐减弱，在射流的卷吸作用下，钻头后方低速流体回流至低压区域，对被射流卷吸的部分流体进行补充，从而导致自驱钻头前后压力梯度减小，自驱钻头的自进力降低；当环空比继续增大至0.75时，后置射流的封隔作用基本失效，自驱钻头前后压力梯度较小。因此，存在最优的环空比，使自驱钻头的自进力最大。
2.2.4 系统压力的影响
图11为后置喷嘴倾角20°、环空比0.53时系统压力对喷头、旋转体和高压软管受力的影响。由图11可知，系统各部分受力与系统压力近似呈线性关系。高压软管主要受到返水阻力，其大小与返水流速有关。环空比一定时，系统压力增加，返流速度增加，高压软管受到的返水阻力增大。涡旋区域和压力梯度的变化影响系统各部分受力。以旋转体受力为例，当系统压力由10 MPa增加至25 MPa时，旋转体受力由16.97 N增加至40.32 N。由数值分析结果(图12)可知，在旋转体后端至前端100 mm范围内，随着系统压力由10 MPa增加至25 MPa，旋转体上方环空压力最小值由73.73 kPa降低至32.38 kPa，旋转体前后压力梯度逐渐增大。压力梯度增大导致旋转体受到的压差力增加。后置喷嘴喷出的高速流体对周围流体形成卷吸，使后置喷嘴出口附近局部压力降低[22]。同时，多股后置射流旋转冲击过程中共同作用形成封隔作用，阻碍流体回流至低压区域。压力梯度作用提高了自驱钻头的自进力。随着系统压力的增加，射流卷吸效果和封隔作用增强，低压区压力逐渐降低，压力梯度形成的推力增大，有利于提高自进力。
![]()
图 11 不同压力条件系统受力变化Figure 11. Change of system forces under different pressure conditions2.3 正交数值模拟结果与分析
根据极差的大小可以判断后置喷嘴倾角、转速、环空比、系统压力对自进力的影响程度。各影响因素中对应不同水平的数值模拟结果的最大值与最小值之差定义为极差。Ki表示任意列上水平号为i时所对应的结果之和，计算9个数值模拟方案的极差结果见表4。从表4可以看出，环空比的极差最大，为300.07，所以影响自进力的最主要因素是环空比；其次是系统压力，极差为111.87；转速的极差为60.42，其对自进力的影响小于环空比和系统压力；后置喷嘴倾角对自进力的影响相对其他几个因素较小。因此得到自进力影响因素主次关系为：环空比>系统压力>转速>后置喷嘴倾角。
表 4 正交数值模拟结果Table 4. Orthogonal numerical simulation results编号/参数 压力/MPa 后置喷嘴
倾角/(°)转速/(r·min−1) 环空比 自进力/N 1 15 20 600 0.44 124.16 2 15 25 900 0.53 60.92 3 15 35 1 200 0.63 32.17 4 20 20 900 0.63 43.07 5 20 25 1 200 0.44 146.74 6 20 35 600 0.53 67.00 7 25 20 1 200 0.53 123.35 8 25 25 600 0.63 50.68 9 25 35 900 0.44 155.09 K1 217.25 290.58 241.84 425.99 K2 256.81 258.34 259.08 251.27 K3 329.12 254.26 302.26 125.92 极差 111.87 36.32 60.42 300.07 3 自进力测试实验
3.1 实验装置
自进力测试实验装置主要由柱塞泵、高压软管、模拟管道、自驱钻头、数显式推拉力计组成，如图13所示。柱塞泵额定压力为35 MPa，额定排量为100 L/min。实验用自驱钻头前置喷嘴为3个直径1 mm喷嘴，前置喷嘴与钻头中轴线夹角分别为35°、30°、10°；后置喷嘴为2个直径1.5 mm喷嘴，与钻头中轴线夹角分别为20°、25°、30°、35°、40°、45°。
3.2 实验方法
实验装置如图13所示。模拟管道水平放置并固定，连接高压软管的自驱钻头放置于模拟管道内，将测试线一端与自驱钻头连接，另一端与数显式推拉力计连接。拉力计固定并确保测试线水平放置。启动柱塞泵，自驱钻头产生推力，拉力计示数即为自进力。
自驱钻头后置喷嘴沿周向呈一定偏心角，高速射流喷射时对钻头施加扭矩实现旋转。实验所用自驱钻头使用阻尼液控制转速，钻头偏心角和射流压力一定时，通过更换不同黏度的阻尼液调整转速。选用VC6236P型高精度数显转速计(图14)进行转速测试实验，测试时利用激光监测被测物体表面的反光纸即可得到转速数值。
分别改变后置喷嘴倾角、转速、环空比、系统压力，进行自进力测试实验，实验方案与正交数值模拟方案一致(表3)。
3.3 实验结果与分析
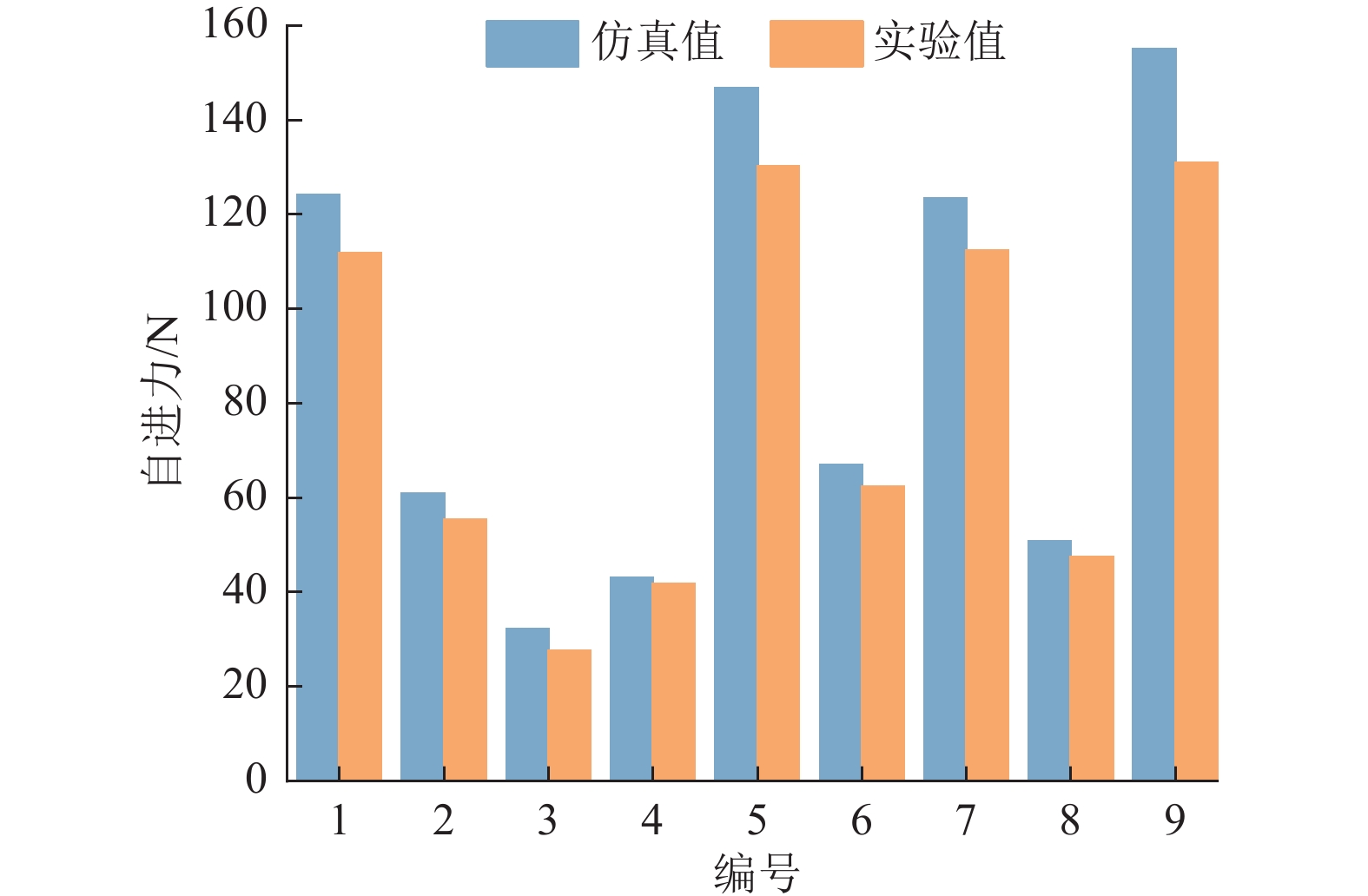
自进力作为衡量自驱钻头结构优劣的关键指标，其大小直接影响自进效果。为验证数值模拟结果的正确性，开展不同条件下自进力测试实验，将自进力的实验结果与数值模拟结果进行对比，如图15所示。由图15可知，自驱钻头自进力实验值和仿真值的变化规律较为一致。在进行数值模拟时，假设自驱钻头和高压软管在管道中的位置固定，但在实验过程中，自驱钻头的旋转过程导致钻头和高压软管的位置发生改变，从而影响管道内的流场和自进力。因此，在相同条件下，自驱钻头自进力仿真值与实验值存在一定误差。由图15可知，自进力数值模拟结果与实验结果之间的最大误差为24.24 N，验证了通过数值模拟结果分析后置喷嘴倾角、转速、环空比和系统压力对自驱钻头自进力影响规律的正确性。
![]()
图 15 自进力实验值与仿真值对比Figure 15. Comparison of experimental and simulated values of self-propelling forces4 结 论
a. 反冲力和压差力是自驱钻头实现自进的主要动力，涡旋挤压碰撞作用和射流卷吸作用导致自驱钻头产生压差力。增大后置喷嘴倾角或提高转速均会增强涡旋挤压碰撞作用，导致钻头所受压差力增加，从而提高自驱钻头自进力。
b. 后置射流旋转冲击过程中产生封隔作用，阻碍钻头后方流体回流至低压区域。提高转速、系统压力或减小环空比均会导致后置射流的封隔作用增强，致使自驱钻头所受压差力增加，有利于提高自驱钻头的自进力。
c. 涡旋区导致水流拖曳力方向发生改变，从而影响返水阻力。采用出口处流速代替返流速度计算返水阻力时忽略了涡旋区的影响，因此综合摩擦因素理论值需要采用系数进行修正。
d. 环空比、系统压力、转速和后置喷嘴倾角影响自驱钻头自进力，极差分别为300.07、111.87、60.42、36.32，影响因素主次关系为：环空比>系统压力>转速>后置喷嘴倾角。
e. 由于计算机运算能力的限制，数值模拟所用模型尺寸较小，无法充分分析钻孔内全孔段流场结构特征及其对管道受力的影响；本文实验设备尚需改进，无法开展大倾角钻孔条件下相关实验。后续拟开展大倾角钻孔条件下数值模拟和实验研究。
-
![]()
图 1 水射流自驱钻头修复钻孔装置
Fig. 1 Borehole restoration device of self-propelled water jet drill bit
![]()
图 4 不同后置喷嘴倾角自进力和返水阻力变化
Fig. 4 Change of self-propelling force and resistance to water backflow at different angles of rear nozzle
![]()
图 6 不同后置喷嘴倾角条件下喷头上方环空压力对比
Fig. 6 Comparison of annular pressure above nozzle at different angles of rear nozzle
![]()
图 7 不同转速条件下射流轴心位置速度变化
Fig. 7 Change of velocity of jet at the axis position at different rotational speeds
![]()
图 15 自进力实验值与仿真值对比
Fig. 15 Comparison of experimental and simulated values of self-propelling forces
表 1 多因素逐项数值模拟方案
Table 1 Scheme of multi-factor numerical simulation by item
编号 后置喷嘴倾角/(°) 转速/(r·min−1) 环空比 压力/MPa 1 20 600 0.63 25 2 25 600 0.63 25 3 30 600 0.63 25 4 35 600 0.63 25 5 40 600 0.63 25 6 45 600 0.63 25 7 20 0 0.63 25 8 20 300 0.63 25 9 20 900 0.63 25 10 20 1200 0.63 25 11 20 900 0.44 25 12 20 900 0.53 25 13 20 900 0.69 25 14 20 900 0.75 25 15 20 900 0.53 10 16 20 900 0.53 15 17 20 900 0.53 20 
下载: 导出CSV
表 2 正交数值模拟因素水平
Table 2 Factors and levels of orthogonal numerical simulation
水平 系统压力/MPa 后置喷嘴倾角/(°) 转速/(r·min−1) 环空比 1 15 20 600 0.44 2 20 25 900 0.53 3 25 35 1 200 0.63
下载: 导出CSV
表 3 正交数值模拟方案
Table 3 Orthogonal numerical simulation scheme
编号 系统压力/MPa 后置喷嘴倾角/(°) 转速/(r·min−1) 环空比 1 15 20 600 0.44 2 15 25 900 0.53 3 15 35 1 200 0.63 4 20 20 900 0.63 5 20 25 1 200 0.44 6 20 35 600 0.53 7 25 20 1 200 0.53 8 25 25 600 0.63 9 25 35 900 0.44
下载: 导出CSV
表 4 正交数值模拟结果
Table 4 Orthogonal numerical simulation results
编号/参数 压力/MPa 后置喷嘴
倾角/(°)转速/(r·min−1) 环空比 自进力/N 1 15 20 600 0.44 124.16 2 15 25 900 0.53 60.92 3 15 35 1 200 0.63 32.17 4 20 20 900 0.63 43.07 5 20 25 1 200 0.44 146.74 6 20 35 600 0.53 67.00 7 25 20 1 200 0.53 123.35 8 25 25 600 0.63 50.68 9 25 35 900 0.44 155.09 K1 217.25 290.58 241.84 425.99 K2 256.81 258.34 259.08 251.27 K3 329.12 254.26 302.26 125.92 极差 111.87 36.32 60.42 300.07
下载: 导出CSV
-
[1] 董书宁,刘再斌,程建远,等. 煤炭智能开采地质保障技术及展望[J]. 煤田地质与勘探,2021,49(1):21−31. DONG Shuning,LIU Zaibin,CHENG Jianyuan,et al. Technologies and prospect of geological guarantee for intelligent coal mining[J]. Coal Geology & Exploration,2021,49(1):21−31.
[2] 刘勇,代硕,魏建平,等. 低压磨料空气射流破硬岩规律及特征实验研究[J]. 岩石力学与工程学报,2022,41(6):1172−1182. LIU Yong,DAI Shuo,WEI Jianping,et al. Experimental study on hard rock breaking laws and characteristics by low−pressure abrasive air jet[J]. Chinese Journal of Rock Mechanics and Engineering,2022,41(6):1172−1182.
[3] 袁亮. 我国深部煤与瓦斯共采战略思考[J]. 煤炭学报,2016,41(1):1−6. YUAN Liang. Strategic thinking of simultaneous exploitation of coal and gas in deep mining[J]. Journal of China Coal Society,2016,41(1):1−6.
[4] 张超林,王恩元,王奕博,等. 近20年我国煤与瓦斯突出事故时空分布及防控建议[J]. 煤田地质与勘探,2021,49(4):134−141. ZHANG Chaolin,WANG Enyuan,WANG Yibo,et al. Spatial–temporal distribution of outburst accidents from 2001 to 2020 in China and suggestions for prevention and control[J]. Coal Geology & Exploration,2021,49(4):134−141.
[5] 梁道富,曹建明,代茂,等. 贵州青龙煤矿碎软煤层区域瓦斯递进式抽采技术[J]. 煤田地质与勘探,2020,48(5):48−52. LIANG Daofu,CAO Jianming,DAI Mao,et al. Progressive gas extraction technology in broken soft coal seam of Qinglong Coal Mine,Guizhou Province[J]. Coal Geology & Exploration,2020,48(5):48−52.
[6] 邹士超,辛嵩. 煤层瓦斯钻孔有效抽采半径研究[J]. 中国安全科学学报,2020,30(4):53−59. ZOU Shichao,XIN Song. Effective extraction radius of gas drilling in coal seam[J]. China Safety Science Journal,2020,30(4):53−59.
[7] 齐庆新,潘一山,舒龙勇,等. 煤矿深部开采煤岩动力灾害多尺度分源防控理论与技术架构[J]. 煤炭学报,2018,43(7):1801−1810. QI Qingxin,PAN Yishan,SHU Longyong,et al. Theory and technical framework of prevention and control with different sources in multi−scales for coal and rock dynamic disasters in deep mining of coal mines[J]. Journal of China Coal Society,2018,43(7):1801−1810.
[8] 刘勇,李志飞,魏建平,等. 磨料空气射流破煤冲蚀模型研究[J]. 煤炭学报,2020,45(5):1733−1742. LIU Yong,LI Zhifei,WEI Jianping,et al. Erosion model of abrasive air jet used in coal breaking[J]. Journal of China Coal Society,2020,45(5):1733−1742.
[9] 刘勇,魏建平,王登科,等. 磨料气体射流冲蚀磨损岩石特征分析[J]. 煤炭学报,2018,43(11):3033−3041. LIU Yong,WEI Jianping,WANG Dengke,et al. Erosive wear characteristic of rock impacted by abrasive gas jet[J]. Journal of China Coal Society,2018,43(11):3033−3041.
[10] 孙龙德,江同文,王凤兰,等. 关于油田寿命的思考[J]. 石油学报,2021,42(1):56−63. SUN Longde,JIANG Tongwen,WANG Fenglan,et al. Thoughts on the development life of oilfield[J]. Acta Petrolei Sinica,2021,42(1):56−63.
[11] LANDERS C. Method of and apparatus for horizontal well drilling: US06125949A[P]. 2000-10-03.
[12] 刘玉洲,陆庭侃,柳晓莉. 煤层气井超短半径自进式水平钻井技术研究[J]. 天然气工业,2006,26(2):69−72. LIU Yuzhou,LU Tingkan,LIU Xiaoli. Self−feeding horizontal drilling technology with super−short radius for coal−bed methane wells[J]. Natural Gas Industry,2006,26(2):69−72.
[13] 刘勇,梁博臣,何岸,等. 自进式旋转钻头钻孔修复理论及关键参数研究[J]. 中国安全生产科学技术,2016,12(2):39−44. LIU Yong,LIANG Bochen,HE An,et al. Research on theory and technical parameter of borehole restoration for self−propelling and rotating drill[J]. Journal of Safety Science and Technology,2016,12(2):39−44.
[14] 贺乐昌. 水力深穿透射孔自进旋转喷头关键参数研究[D]. 哈尔滨: 哈尔滨工业大学, 2009. HE Lechang. Study on key parameters of self–propelled rotatory nozzle for water−jet deep penetrating perforation[D]. Harbin: Harbin Institute of Technology, 2009.
[15] 董惠娟,白良浩,吕岩,等. 自进式高压水射流破岩数值模拟分析[J]. 石油机械,2010,38(12):29−33. DONG Huijuan,BAI Lianghao,LYU Yan,et al. A numerical simulation analysis of self–propelled high–pressure water jet rock breaking[J]. China Petroleum Machinery,2010,38(12):29−33.
[16] 郭瑞昌,李根生,黄中伟,等. 多孔式射流钻头流场数值模拟研究[J]. 流体机械,2010,38(4):13−17. GUO Ruichang,LI Gensheng,HUANG Zhongwei,et al. Numerical simulation study on flow field of multi–hole jet bit[J]. Fluid Machinery,2010,38(4):13−17.
[17] 刘勇, 代硕, 魏建平, 等. 自进式钻头钻孔修复运动方程及关键参数研究[J/OL]. 河南理工大学学报 (自然科学版), 2022: 1–11 [2023-01-06]. http://kns.cnki.net/kcms/detail/41.1384.N.20220530.1046.002.html. LIU Yong, DAI Shuo, WEI Jianping, et al. Research on equations of motion and technical parameter of borehole restoration for self−propelling drill[J/OL]. Journal of Henan Polytechnic University (Natural Science), 2022: 1–11[2023-01-06]. http://kns.cnki.net/kcms/detail/41.1384.N.20220530.1046.002.html.
[18] 祝效华,陈伟. 自进式喷头自进力影响因素分析及参数优化[J]. 水动力学研究与进展,2018,33(1):89−97. ZHU Xiaohua,CHEN Wei. Analysis on influencing factors of self−propelled force and parameters optimization of the jet nozzle[J]. Chinese Journal of Hydrodynamics,2018,33(1):89−97.
[19] ZHANG X,LIU X,GENG D,et al. Numerical simulation on the flow field of self–propelled multi–orifices nozzle for ultra–short radius radial jet drilling[J]. International Journal of Oil,Gas and Coal Technology,2018,17(1):1−11. DOI: 10.1504/IJOGCT.2018.089338
[20] 莫丽,王军. 自推进喷嘴井筒内流场数值模拟[J]. 中南大学学报 (自然科学版),2015,46(10):3656−3662. MO Li,WANG Jun. Numerical simulation for wellbore flow field of self–propelled nozzle[J]. Journal of Central South University (Science and Technology),2015,46(10):3656−3662.
[21] PENG Haojun,ZHANG Ping. Numerical simulation of high speed rotating waterjet flow field in a semi enclosed vacuum chamber[J]. Computer Modeling in Engineering & Sciences,2018,114(1):59−73.
[22] 张欣玮,汤积仁,卢义玉,等. 淹没条件下水射流涡旋特性大涡模拟及实验研究[J]. 中国石油大学学报 (自然科学版),2015,39(3):98−104. ZHANG Xinwei,TANG Jiren,LU Yiyu,et al. Large eddy simulation and experimental study on vortex characteristics of water jet in submerged condition[J]. Journal of China University of Petroleum (Edition of Natural Science),2015,39(3):98−104.
-
期刊类型引用(5)
1. 童校长，文虎，徐鹤翔，刘厅，温鸿达，程小蛟. 地面井掏煤造穴卸压增透技术及工程应用. 西安科技大学学报. 2025(01): 61-73 . 
百度学术
2. 石光. 高压水射流割缝钻头的研制与增透效果工程验证. 煤. 2024(04): 6-10 . 百度学术
3. 刘勇，李阳，魏建平，苑永旺，代硕，李林豫. 自驱修孔钻头动力参数及钻齿结构研究. 煤田地质与勘探. 2024(04): 179-189 . 本站查看
4. 魏建平，李翔，刘勇，沈荷莲，李海超，高梦雅. 自激振荡脉冲SC-CO_2射流冲击频率调制. 煤炭学报. 2024(06): 2675-2690 . 百度学术
5. 杨展，谭松成，杨凯华，方小红. 基于有限元分析的组合式金刚石钻头磨损规律与设计研究. 煤田地质与勘探. 2023(09): 164-170 . 本站查看
其他类型引用(1)
计量
- 文章访问数: 191
- HTML全文浏览量: 18
- PDF下载量: 33
- 被引次数: 6
