Research and application of fracture mechanics model of stope roof under the coupling of direct roof and basic roof
-
摘要:
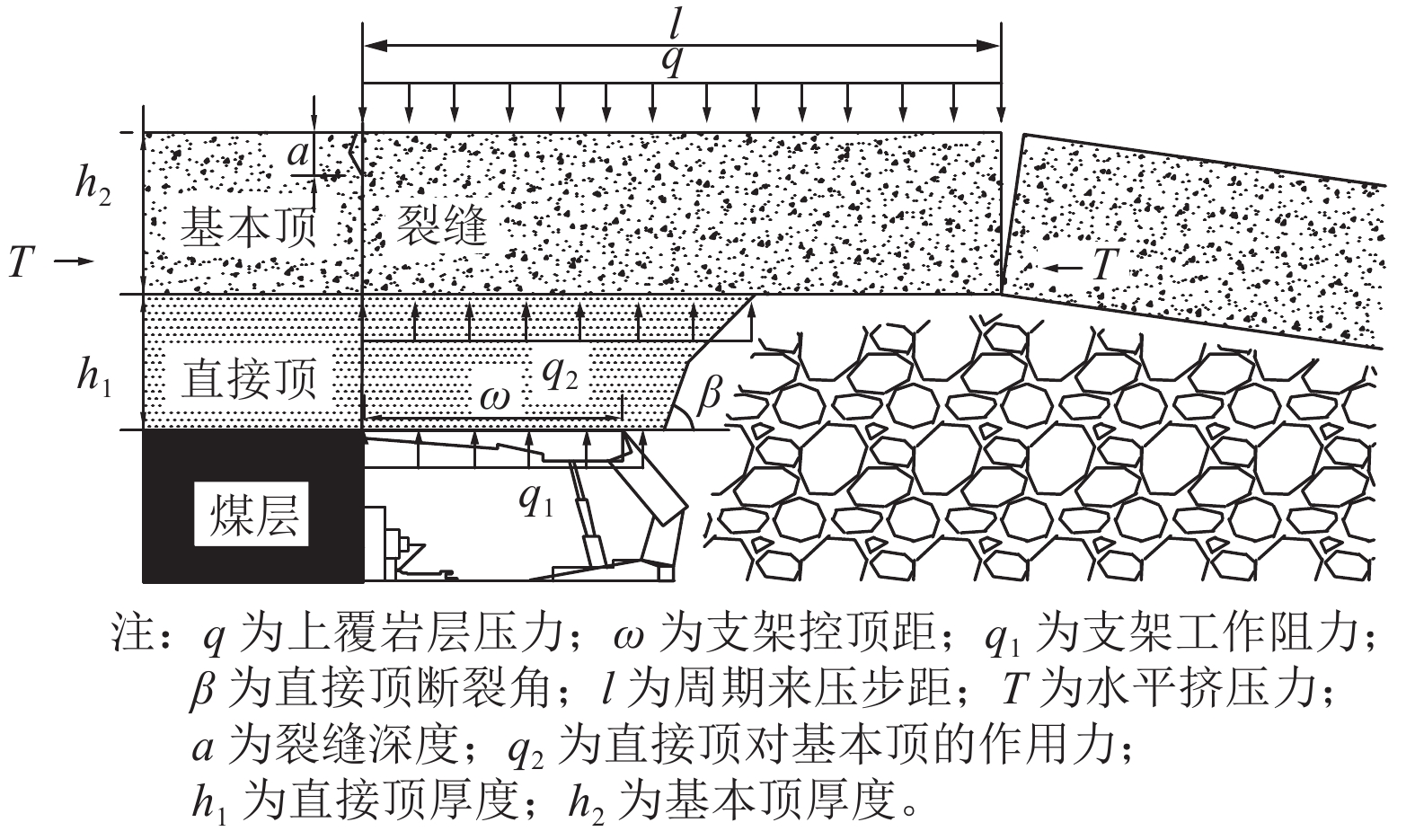
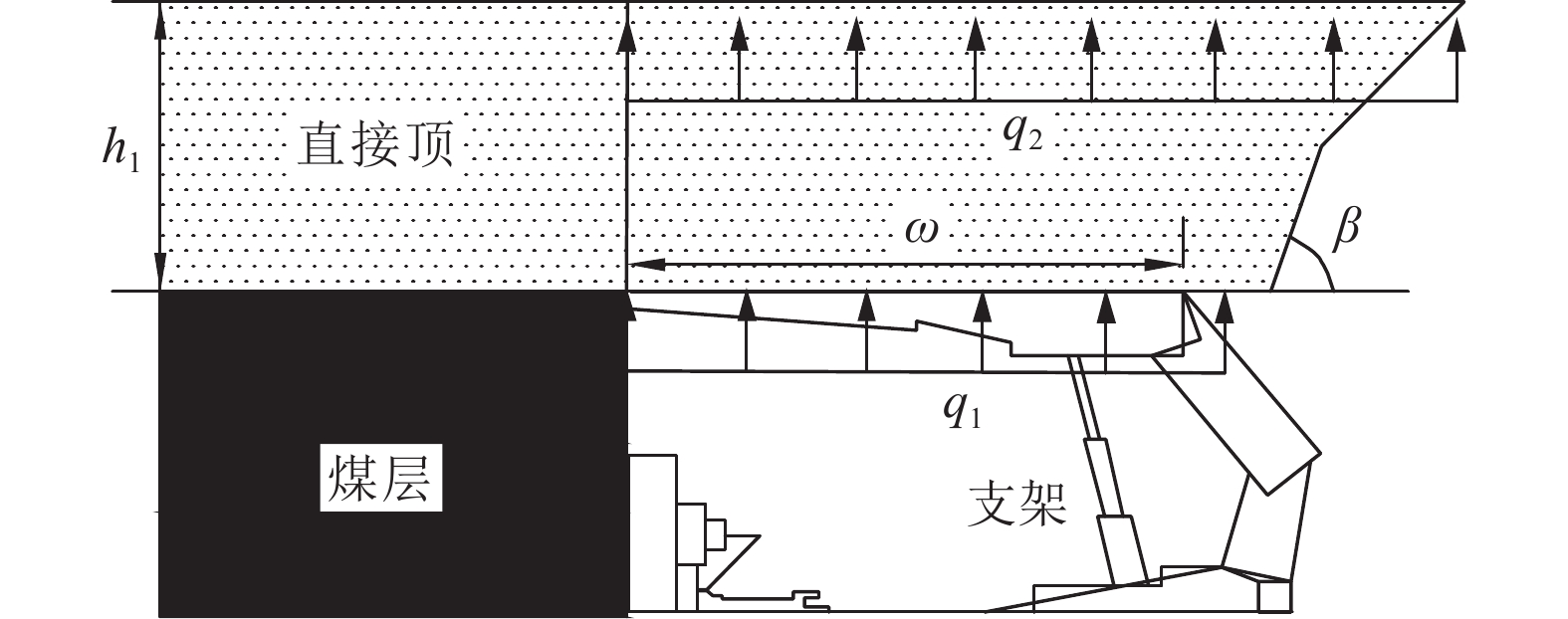
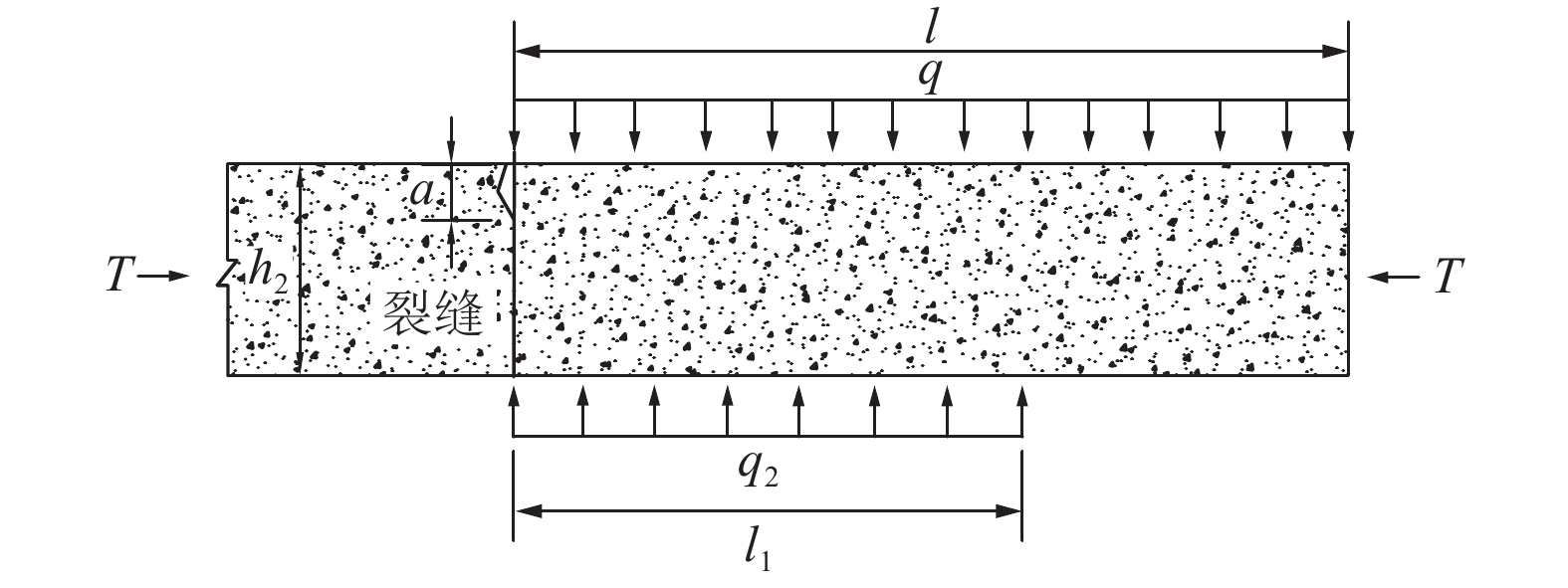
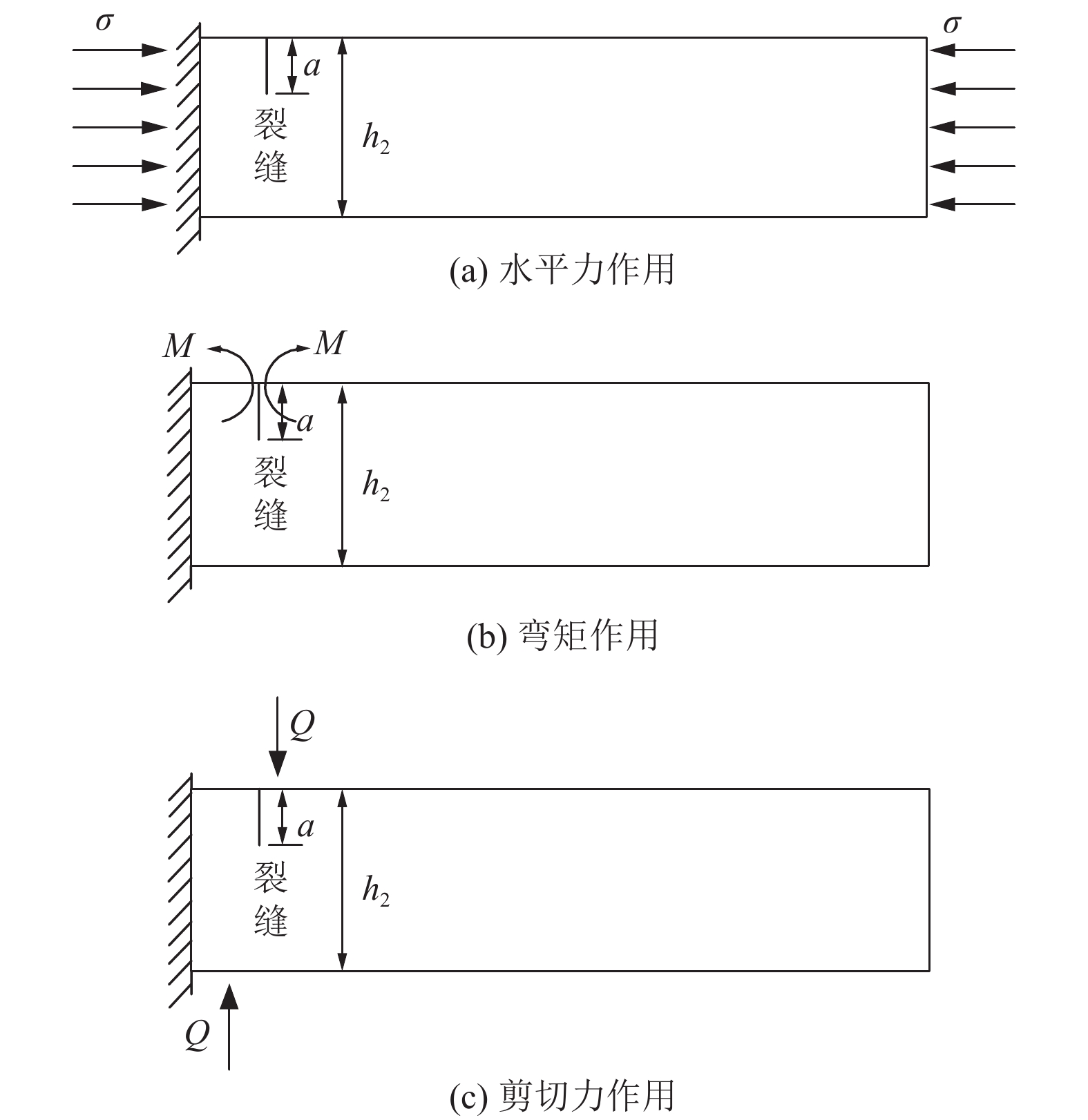
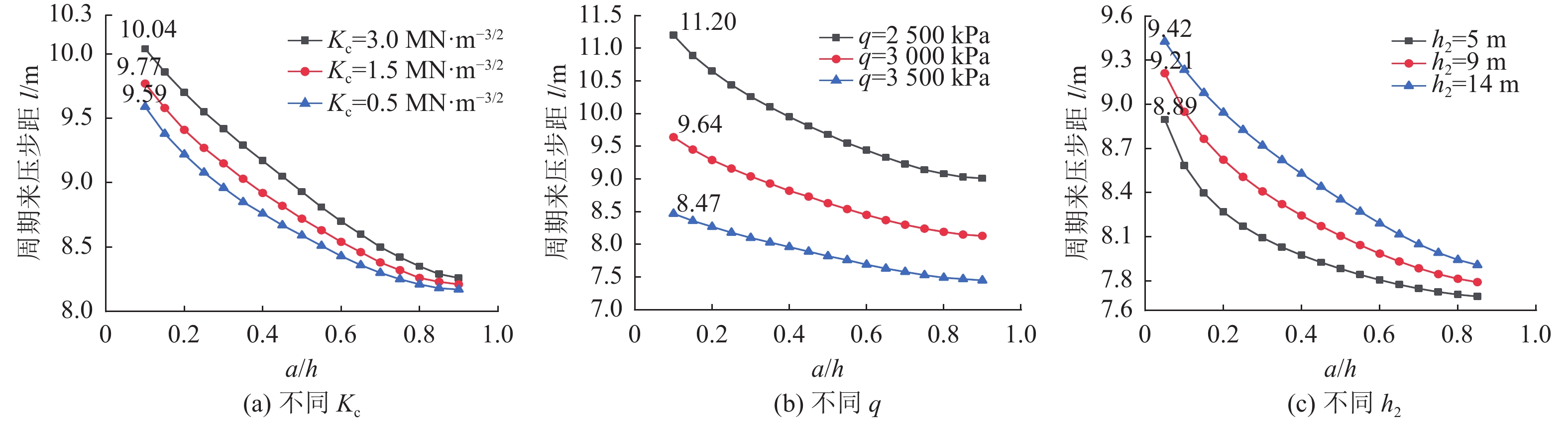
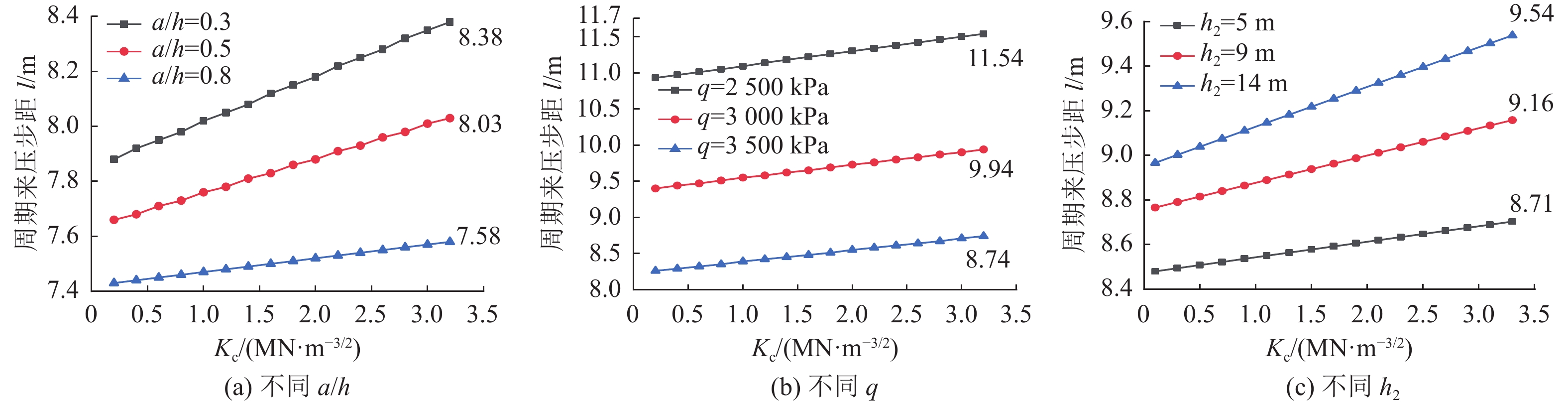
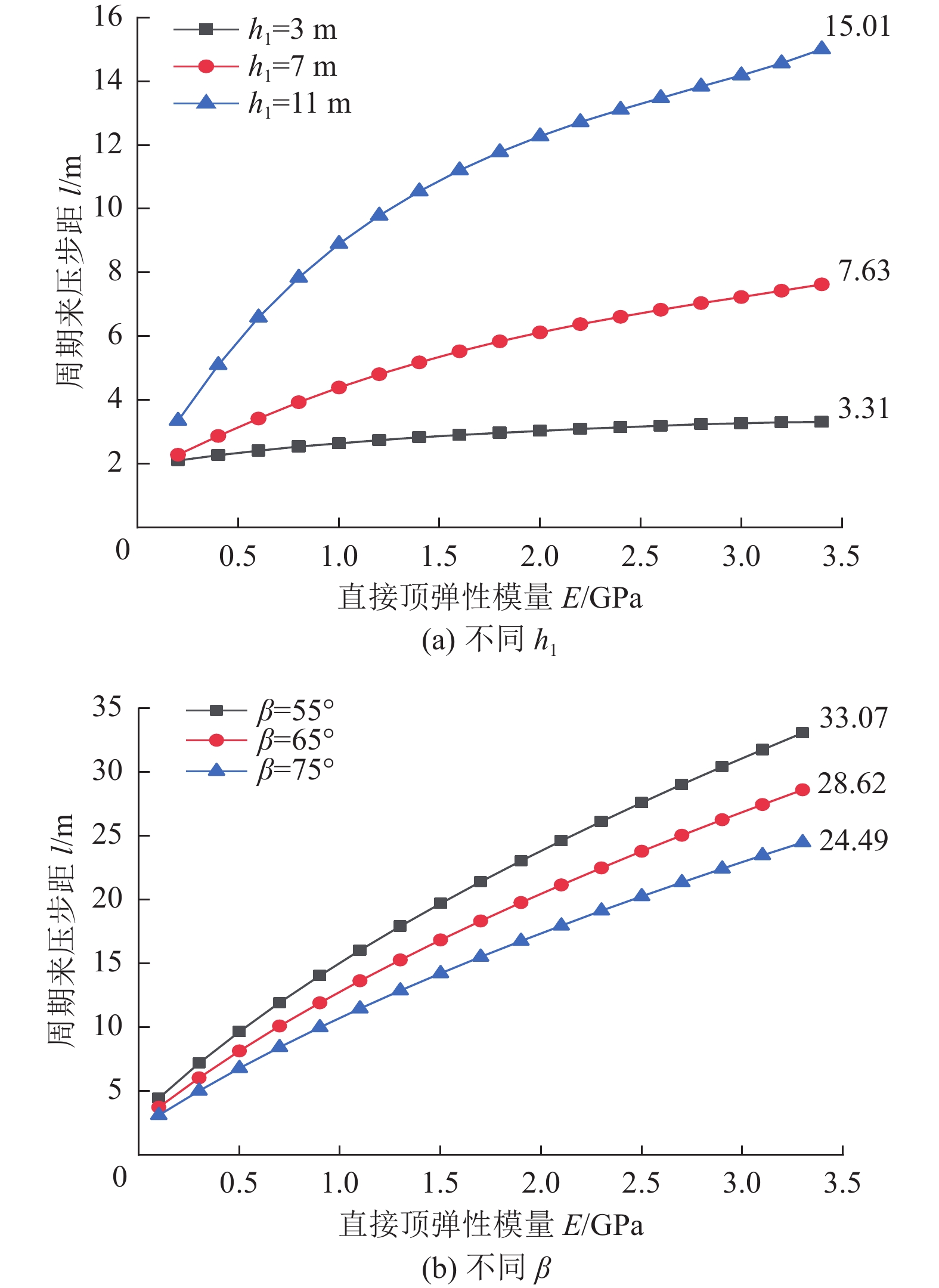
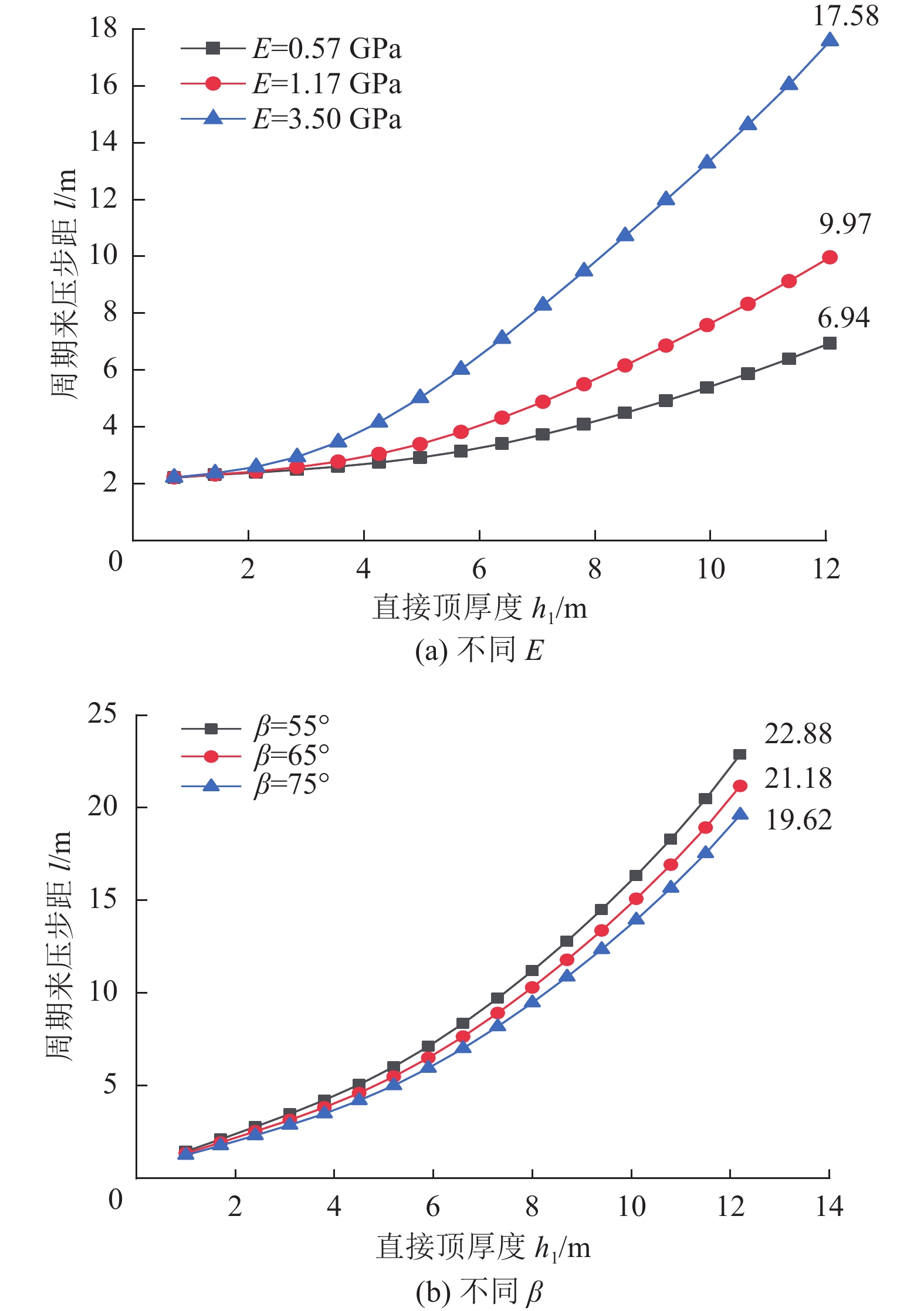
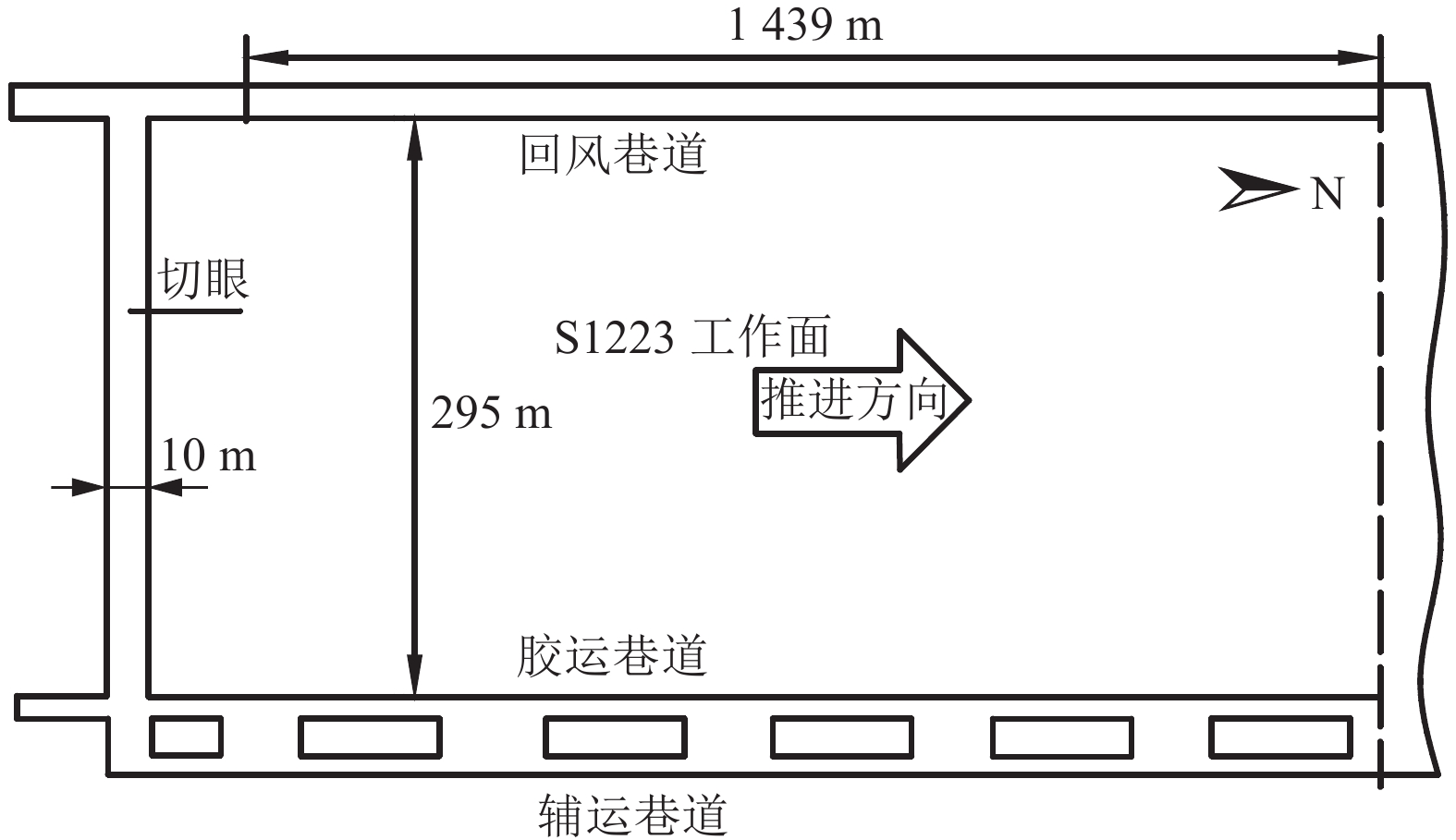
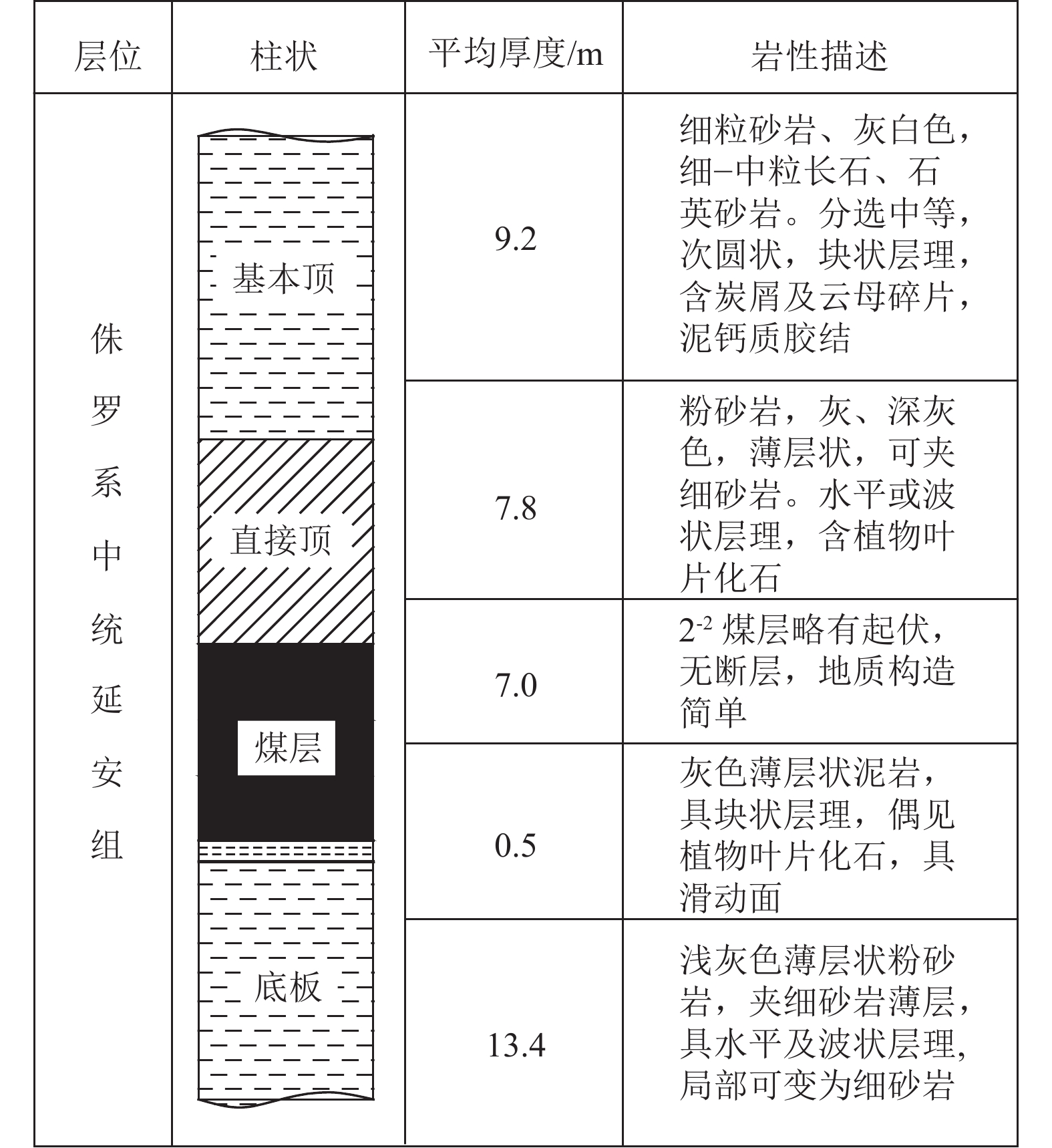
周期来压是矿山压力显现的典型特征，准确进行采场周期来压步距预测是有效降低采场事故发生的重要途径。针对基本顶自身缺陷与直接顶耦合作用对周期来压步距的影响，视采场顶板为自带裂缝的有限板模型，根据覆岩协调变形机理，基于断裂力学理论建立采场顶板断裂力学模型，推导直接顶−基本顶耦合作用下周期来压步距函数式，以陕北某矿区2个工作面为例，分析基本顶岩石断裂韧度、裂缝深度、直接顶厚度和弹性模量等参数对周期来压步距的作用规律。研究表明：基本顶断裂韧度与周期来压步距呈近似线性关系；裂缝深度比(裂缝深度/顶板厚度)对周期来压步距影响较大，裂缝深度比达到0.8后，基本顶失稳破坏；直接顶厚度小于3 m时对周期来压步距影响较小，超过3 m后对周期来压步距影响显著。研究结果对采场顶板周期来压步距预测及支架选型具有重要的理论意义和工程价值。
Abstract:Periodic weighting is a typical characteristic of mine pressure. Accurate prediction of stope periodic weighting step is an important way to effectively reduce the occurrence of stope accidents. Aiming at the influence of the coupling between the basic roof defects and the direct roof on the periodic weighting step, the stope roof was regarded as a finite plate model with cracks. According to the coordinate deformation mechanism of the overburden rock, the fracture mechanics model of the stope roof was established based on the fracture mechanics theory. On this basis, the periodic weighting step function under the coupling between the direct roof and basic roof was derived. In addition, the influence of the parameters such as the fracture toughness of the basic roof rock, crack depth, direct roof thickness and elastic modulus on the periodic weighting step was analyzed based on 2 working faces of a mine area in northern Shaanxi. The research shows that: (1) The fracture toughness of the basic roof is in approximately linear relation with the periodic weighting step. (2) The crack depth ratio (crack depth/roof thickness) has a great influence on the periodic weighting step. In particular, the basic roof is unstable and destroyed when the crack depth ratio reaches 0.8. (3) The direct roof with the thickness less than 3 m has little effect on the periodic weighting step, but that with the thickness greater than 3 m has a significant effect on the periodic weighting step. Generally, the research results have important theoretical significance and engineering value for the prediction of periodic weighting step of stope roof and the selection of support.
-
随着石油钻井技术的发展，自动化、智能化成为其未来的发展趋势，但目前较低的井下信息上传速率难以满足自动化、智能化钻井的需要[1-2]。因此，井下信息高速传输技术成为关键。在井下信息高速传输技术中，钻井液压力波信息传输技术具有鲁棒性强、成本低等优点，具有广阔的应用前景[3]。由于钻井工况的复杂性，钻井液压力波在传输过程中存在较大的衰减，阻碍了其传输速率的提升[4]。因此，研究钻井液压力波的衰减特性对提升其传输速率具有重要意义。
早期关于钻井液压力波衰减的研究以采用现场数据拟合经验公式为主，其特点是公式较为简洁，但由于缺乏理论支持，适应范围有限，难以进行推广[5]。后续相关研究主要从时域及频域开展，时域方面的研究主要是基于流体动量方程，构建井筒中压力与时间的关系，结合边界条件及初始条件求解各时刻井筒中不同位置的压力，通过将压力波发生器阀前压力值与上游其他位置的压力值对比，研究钻井液压力波的衰减特性[3-4,6-12]，特点是适用于描述不同频率的钻井液压力波的衰减，不足之处在于难以直观获得钻井液压力波衰减量与信号参数及钻井参数的关系。频域方面的研究主要是基于水击理论，采用传输线方法，推导压力波沿井筒的衰减模型，以获取衰减系数[13-16]。但后续研究表明，水击理论可较好地描述低频压力波(<1 Hz)的传输，但对于高频钻井液压力波传输描述的精度较差[17]。
由文献调研可以看出，目前对于低频压力波衰减的研究较为透彻，但相关理论难以直接应用于高频压力波。而目前采用的钻井液压力波频率通常位于高频段，开展高频压力波衰减特性的研究具有重要意义。
针对高频钻井液压力波衰减问题，为了探明其衰减规律，基于二维轴对称瞬态流动理论，构建高频压力波衰减模型，以描述衰减与信号参数及钻井参数的关系，并采用地面实验验证该模型。随后利用该模型分析钻井液压力波频率、压力波传输距离、钻井液密度及黏度、钻柱内径对衰减的影响，以期为开发高频钻井液压力波信息传输技术提供理论基础。
1 数学模型
1.1 信息传输系统
钻井液压力波信息传输系统如图1所示。该系统主要包含钻井泵、空气包、压力传感器、压力波发生器及钻头。钻井泵通常采用三缸往复泵，其排量可视为恒定值。空气包为包含压缩空气的容器，可用于吸收钻井泵产生的高频压力波动以提升钻井泵的性能。压力传感器安装在井口处，用于检测上传的钻井液压力波。压力波发生器通过周期性地改变阀口面积，堵塞钻井液的流通路径从而产生压力波。
![]()
图 1 钻井液压力波信息传输系统Figure 1. Drilling fluid pressure wave information transmission system当钻井液压力波信息传输系统工作时，钻井泵排量逐步增加至指定排量，待排量稳定后，压力波发生器工作产生压力波，携带井下信息传输至井口，井口压力传感器检测压力波后将其传输至信号处理单元进行处理并解释，最终还原出井下信息。在传输过程中，钻井液压力波存在较大的衰减，本文重点探究高频压力波沿井筒的衰减机理，及衰减量与信号参数和钻井参数的关系。
为便于描述，对后续章节做如下约定：(1)坐标系为极坐标，原点位于井口钻柱中心，沿钻柱轴线向下为x正向，沿钻柱半径向外为r方向。(2)压力波传输距离定义为压力波发生器与井口压力传感器间的距离。(3)假设同一钻柱截面钻井液压力值相等。
1.2 衰减模型
井筒中高频钻井液压力波衰减[18]可表示为：
$$ p(x) = {p_0}{{\rm{exp}}{ (- \alpha x)}} $$ (1) 式中：
$p(x)$ 为立管压力；$x$ 为钻井液压力波发生器与传感器间的距离；${{\rm{exp}}{ (- \alpha x)}}$ 为衰减系数，定义为传感器处立管压力与压力波发生器产生的压力波幅值之比；${p_0}$ 为压力波发生器处产生的压力。研究高频钻井液压力波衰减的关键在于确定衰减系数。基于二维轴对称瞬态流动理论，钻柱内流体运动方程[17]可写为：
$$ {\rho _0}\frac{{\partial v}}{{\partial t}} + \frac{{\partial p}}{{\partial x}} - \frac{\eta }{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial v}}{{\partial r}}} \right) = 0 $$ (2) 式中：
$p$ 为瞬态立管压力；$t$ 为时间；${\rho _0}$ 为钻井液密度；$v$ 为钻柱内钻井液瞬态流速；$\eta $ 为钻井液的动力黏度；$r$ 为钻柱径向某点至钻柱中心的距离。因压力波动与钻井液流速波动均由压力波发生器工作引起，故二者具有相同的波动频率。令：
$$ p = {p_{\rm{m}}}(x){{\rm{exp}}{({{{\rm{j}}}}\omega t)}} $$ (3) $$ v = {v_{\rm{m}}}(r,x){{\rm{exp}}{({\rm{j}}\omega t)}} $$ (4) 式中：
${p_{\rm{m}}}$ 为压力波动的幅值；$\omega $ 为压力波角频率；${v_{\rm{m}}}$ 为钻井液流速的幅值；${\rm{j}}$ 为虚数单位，且${{\rm{j}}^2} = - 1$ 。将式(3)、式(4)代入式(2)得：
$$ \left( {\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + {K^2}} \right){v_{\rm{m}}} = \frac{1}{\eta }\frac{{\partial {p_{\rm{m}}}}}{{\partial x}} $$ (5) 其中，
${K^2} = {\rm{j}}\dfrac{{{\rho _0}\omega }}{\eta }$ 。式(5)的特解为：
$$ {v_{\rm{m}}} = \frac{1}{{\eta {K^2}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial x}} $$ (6) 此时式(5)变为标准零阶贝塞尔方程，可得其通解为：
$$ {v_{\rm{m}}} = A{J_0}(Kr) + B{N_0}(Kr) + \frac{1}{{\eta {K^2}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial x}} $$ (7) 式中：A、B均为待确定系数；
${J_0}$ 为零阶贝塞尔函数；${N_0}$ 为诺伊曼函数。由流体动力学理论可知，当r= 0时，钻井液流速为有限值，此时诺伊曼函数发散，所以B= 0。当
$r = \dfrac{d}{2}$ 时，钻井液流速为0，即${v_{\rm{m}}} = 0$ ，由此可以得出：$$ A = - \frac{1}{{{J_0}(Kd/2)}}\frac{1}{{\eta {K^2}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial x}} $$ (8) 式中：
$d$ 为钻柱内径。将系数
$A$ 和$B$ 代入式(7)可得：$$ {v_{\rm{m}}} = \frac{1}{{\eta {K^2}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial x}}\left[ {1 - \frac{{{J_0}(Kr)}}{{{J_0}(Kd/2)}}} \right] $$ (9) 钻柱某一截面钻井液平均流速可写为：
$$ {{\bar v_{\rm{m}}}} = \frac{4}{{{\text{π}}{d^2}}}\int_0^{\tfrac{d}{2}} {2{\text{π}}r{v_{\rm{m}}}{\rm{d}}r = } \frac{1}{{\eta {K^2}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial x}}\left[ {1 - \frac{{4{J_1}\left(K\dfrac{d}{2}\right)}}{{Kd{J_0}\left(K\dfrac{d}{2}\right)}}} \right] $$ (10) 式中：J1为一阶贝塞尔函数。
假设钻柱内径满足
$d > 20\sqrt {\dfrac{\eta }{{{\rho _0}\omega }}}$ ，由贝塞尔函数大宗量近似可以得出$\dfrac{{{J_1}\left(K\dfrac{d}{2}\right)}}{{{J_0}\left(K\dfrac{d}{2}\right)}} \approx - {\rm{j}}$ ，此时式(10)可写为：$$\begin{aligned} & - \frac{{\partial {p_{\rm{m}}}}}{{\partial x}} \approx - \eta {K^2}\left( {1 - {\rm{j}}\frac{4}{{Kd}}} \right) {{\bar v_{\rm{m}}}} = \\ &\qquad \left[ {{\rm{j}}{\rho _0}\omega + \frac{{2\sqrt {2\eta {\rho _0}\omega } }}{d}(1 + {\rm{j}})} \right] {{\bar v_{\rm{m}}}} \end{aligned} $$ (11) 记
$\rho = {\rho _0}\left( {1 + \dfrac{2}{d}\sqrt {\dfrac{{2\eta }}{{{\rho _0}\omega }}} } \right)$ ，$R = \dfrac{2}{d}\sqrt {2\eta {\rho _0}\omega }$ ，式(11)可写为：$$ - \frac{{\partial {p_{\rm{m}}}}}{{\partial x}} = ({\rm{j}}\rho \omega + R) {{\bar v_{\rm{m}}}} $$ (12) 将式(3)和式(4)代入式(12)可得：
$$ - \frac{{\partial p}}{{\partial x}} = \rho \frac{{\partial \bar v }}{{\partial t}} + R\bar v $$ (13) 式中：
$\bar v $ 为钻井液流速的平均值。当存在压力波动，钻井液物态方程和连续性方程仍成立，钻井液物态方程和连续性方程可写为：
$$ p = {c^2}\rho $$ (14) $$ \rho \frac{{\partial \bar v }}{{\partial x}} = - \frac{{\partial \rho }}{{\partial t}} $$ (15) 式中：
$c$ 为压力波波速。联立式(13)—式(15)可得：
$$ \rho c\frac{{{\partial ^2}\bar v }}{{\partial {x^2}}} = \rho \frac{{{\partial ^2}\bar v }}{{\partial {t^2}}} + R\frac{{\partial \bar v }}{{\partial t}} $$ (16) 将式(4)代入式(16)可得：
$$ \frac{{{\partial ^2}\bar v }}{{\partial {x^2}}} = \left( { - \frac{{{\omega ^2}}}{{{c^2}}} + {\rm{j}}\frac{{\omega R}}{{\rho {c^2}}}} \right) {{\bar v_{\rm{m}}}} $$ (17) 设
${{\bar v_{\rm{m}}}} = {{\bar v_0}} {{\rm{exp}}{({\rm{j}}k'x)}}$ ，此处$k' = k - {\rm{j}}\alpha$ ，代入式(17)可得：$$ \frac{{{\omega ^2}}}{{{c^2}}} - {\rm{j}}\frac{{\omega R}}{{\rho {c^2}}} = - {\alpha ^2} - 2{\rm{j}}\alpha k + {k^2} $$ (18) 式中：
${{\bar v_0}}$ 为井口处钻井液平均流速幅值；k为钻柱内钻井液压力波的波数；α为钻柱黏滞吸收系数。由于
$\alpha \ll k$ ，化简上式并求解可得：$$ k = \frac{\omega }{c} $$ (19) $$ \alpha = \frac{{\omega R}}{{2\rho {c^2}k}} = \frac{1}{{dc}}\sqrt {\frac{{2\eta \omega }}{\rho }} \approx \frac{1}{{dc}}\sqrt {\frac{{2\eta \omega }}{{{\rho _0}}}} $$ (20) 由此可以得出，当钻井液压力波频率满足
$f > \dfrac{{400\eta }}{{2\pi {\rho _0}{d^2}}}$ 时，钻井液压力波衰减可表述为：$$ p(x) = {{\rm{exp}}\left({ - \frac{x}{{dc}}\sqrt {\frac{{2\eta \omega }}{{{\rho _0}}}} }\right)}{p_0} $$ (21) 例如，当钻柱内径为108.62 mm，钻井液密度为1 340 kg/m3，钻井液黏度为0.060 3 Pa·s时，频率高于0.24 Hz的钻井液压力波的衰减均满足式(21)。
2 模型实验验证
本节采用地面实验验证模型的正确性，地面实验装置如图2所示。实验时泥浆泵安装在压力波发生器上游，其类型为三缸往复泵，可产生几乎恒定的排量。压力波发生器固定在钻柱内，钻柱内径为112 mm。在压力波发生器的下游安装有可调节流量阀，用于模拟钻头的影响。在泥浆泵出口、压力波发生器入口端及出口端分别安装有压力传感器，用于采集不同位置处的钻井液压力波。泥浆泵端压力传感器与入口端压力传感器距离为1 000 m。实验时泥浆泵排量设定为28 L/s，待泥浆泵工作40 s后启动压力波发生器，压力波发生器可产生频率为5 Hz的钻井液压力波，压力传感器分别采集井口及压力波发生器处的压力。实验中采用的钻井液密度为1 340 kg/m3，黏度为0.060 3 Pa·s。
![]()
图 2 地面实验装置1—水箱；2—泥浆泵；3—流量计；4—井口压力传感器；5—入口端压力传感器；6—压力波发生器；7—出口端压力传感器；8—可调节流量阀；9—计算机Figure 2. Ground experiment equipment井口处与压力波发生器上游压力传感器采集的压力波波形经滤波处理后如图3所示。由图可以看出，压力波发生器入口处压力最大值为10.40 MPa，该波形最小值为3.66 MPa，压力波幅值为3.37 MPa。井口处压力最大值为8.60 MPa，该波形最小值为3.83 MPa，压力波幅值为2.38 MPa，衰减系数为0.706。将实验参数代入式(20)可得理论衰减系数为0.684。与实验结果相比，误差为3.12%。
![]()
图 3 发生器入口压力与井口压力对比Figure 3. Comparison of generator inlet pressure and wellhead pressure不同频率下理论衰减系数与实验对比结果如图4所示。由图可以看出，随着频率的增加，理论衰减系数与实验结果误差不断减小。当频率为5 Hz时，理论衰减系数与实验结果的误差为3.12%，当频率为40 Hz时，误差仅为1.43%。由此可以说明，该模型可较好地描述高频钻井液压力波的衰减。
![]()
图 4 不同频率下理论衰减系数与实验结果对比Figure 4. Comparison of theoretical attenuation coefficient and experiment at different frequencies3 分析与讨论
本节基于高频钻井液压力波衰减模型分析信号参数及钻井参数对压力波衰减的影响。为简化分析，下述仿真时均假设井下钻井液压力波为固定频率的正弦波，且幅值为1 MPa。井筒几何参数与钻井液参数均取自文献[17]中的现场数据。
首先分析钻井液压力波衰减与压力波频率的关系。分析时信号参数及钻井参数见表1。钻井液压力波衰减随频率变化规律如图5所示。 由图可以看出，随着频率的增加，井口钻井液压力波幅值逐渐减小，且变化趋势近似为指数。在1~5 Hz频率段内，井口钻井液压力波幅值变化剧烈，随着频率的增加，井口钻井液压力波幅值变化量逐渐减小，当频率高于8 Hz后，井口钻井液压力波幅值变化缓慢且逐渐减小，变化率最大值为0.1262 MPa/Hz。由于频率的升高会导致钻井液压力波衰减量增大，为保证井口处钻井液压力波质量，可采用低频钻井液压力波传输井下数据。
表 1 井口钻井液压力波幅值随频率变化仿真参数Table 1. Simulation parameters for variation of drilling fluid pressure wave amplitude at wellhead with different frequencies密度ρ/
(kg·m−3)动力黏度
η/(Pa·s)压力波频率
f/Hz钻柱内径
d/mm传输距离
x/m1 340 0.060 3 1~40 112 4 430 ![]()
图 5 井口钻井液压力波幅值随频率变化Figure 5. Variation of drilling fluid pressure wave amplitude at wellhead with frequency随后分析钻井液压力波衰减与压力波传输距离的关系。仿真条件见表2，结果如图6所示。由图可以看出，随着传输距离的增加，井口钻井液压力波幅值逐渐减小，变化趋势近似为指数，但变化速率较频率变化时显著减小。随着传输距离的增加，井口钻井液压力波幅值变化速率逐渐减小，当传输距离为1 000 m时，井口钻井液压力波幅值变化率为2.6×10−4 MPa/m，当传输距离为7000 m时，井口钻井液压力波幅值变化率为2.6×10−5 MPa/m，井口钻井液压力波幅值随传输距离的变化率最大为3.802 3×10−4 MPa/m。
表 2 井口钻井液压力波幅值随传输距离变化仿真参数Table 2. Simulation parameters of drilling fluid pressure wave amplitude at wellhead with transmission distance密度
ρ/(kg·m−3)动力黏度
η/(Pa·s)压力波频率
f/Hz钻柱内径
d/mm传输距离
x/m1 340 0.060 3 5 112 0~10 000 ![]()
图 6 井口钻井液压力波幅值随传输距离变化Figure 6. Variation of pressure wave amplitude at wellhead with transmission distance产生上述现象的原因是随着传输距离的增加，连续波信号传输距离增加，由于钻柱壁面摩擦及流体分子间摩擦消耗的能量增加，使得井口位置接收到的压力波信号的幅值显著减小。结合图5可以看出，随着井深的增加，可通过适当减小钻井液压力波频率减小其衰减，从而保证井口处接收到的信号质量。
钻井液压力波衰减随钻井液密度变化如图7所示，仿真参数见表3，钻井液密度变化范围为1 000~2 000 kg/m3[19]。由图可以看出，在高密度钻井液中井口接收到的钻井液压力波幅值较低密度钻井液环境中的大。当钻井液密度为1 000 kg/m3时，井口接收到的钻井液压力波幅值为0.142 MPa，当钻井液密度为2 000 kg/m3时，井口接收到的钻井液压力波幅值为0.252 MPa，这是由于随着钻井液密度的增大，压力波传输过程中质点间摩擦减小，钻井液压力波能量损失降低，使得井口位置处信号幅值增大。同时，随着钻井液密度的增加，井口接收到的钻井液压力波幅值随钻井液密度的变化率逐渐减小，当钻井液密度由1 000 kg/m3变化至1 010 kg/m3时，井口接收到的钻井液压力波幅值增加0.001 38 MPa，当钻井液密度由1 990 kg/m3变化至2 000 kg/m3时，井口接收到的钻井液压力波幅值增加0.000 87 MPa，钻井液压力波幅值随钻井液密度的变化率最大为1.386 7 ×10−4 MPa/(kg·m−3)，由此可以说增加钻井液密度可在一定程度上增强井口信号强度，但增强的程度随钻井液密度增加逐渐减小。
![]()
图 7 井口钻井液压力波幅值随钻井液密度变化Figure 7. Variation of drilling fluid pressure wave amplitude at wellhead with the drilling fluid density表 3 井口钻井液压力波幅值随密度变化仿真参数Table 3. Simulation parameters for variation of drilling fluid pressure wave amplitude at wellhead with drilling fluid density密度ρ/
(kg·m−3)动力黏度η/(Pa·s) 压力波频率f/Hz 钻柱内径d/mm 传输距离x/m 1 000~2 000 0.060 3 5 112 4 430 钻井液压力波衰减随钻井液黏度变化如图8所示，仿真条件见表4，仿真时钻井液动力黏度变化范围为0.02~0.06 Pa·s[20]。由图可以看出，在高黏度钻井液中井口接收到的钻井液压力波强度小于在低黏度钻井液中的井口接收到的钻井液压力波强度，当钻井液黏度为0.02 Pa·s时，井口钻井液压力波幅值为0.379 MPa，当钻井液黏度增至0.06 Pa·s时，井口钻井液压力波幅值为0.186 MPa。衰减量随黏度的最大变化率为0.009 MPa/(Pa·s)。产生上述现象的原因是随着钻井液黏度的增加，压力波传播时因钻柱壁面及流体质点间摩擦造成的能量损失增大，使得井口接收到的压力波幅值显著减小。因此，在现场应用时，为减小信号的衰减应尽量采用低黏度钻井液。
![]()
图 8 井口钻井液压力波幅值随钻井液黏度变化Figure 8. Variation of drilling fluid pressure wave amplitude at wellhead with drilling fluid viscosity表 4 井口钻井液压力波幅值随黏度变化仿真参数Table 4. Simulation parameters for variation of drilling fluid pressure wave amplitude at wellhead with drilling fluid viscosity密度
ρ/(kg·m−3)动力黏度
η/(Pa·s)压力波频率
f/Hz钻柱内径
d/mm传输距离
x/m1 340 0.02~0.06 5 112 4 430 井口钻井液压力波幅值随钻柱内径变化如图9所示，仿真参数见表5。仿真时采用的钻柱尺寸参照API标准。由图可以看出，随着钻柱内径的增大，井口钻井液压力波幅值逐渐增大。当钻柱内径为0.046 1 m时，井口钻井液压力波幅值为0.16 MPa，当钻柱内径为0.149 9 m时，井口钻井液压力波幅值为0.57 MPa，由此可以说明，内径较大的钻柱更有利于钻井液压力波的传输。
![]()
图 9 井口钻井液压力波幅值随钻柱内径变化Figure 9. Variation of drilling fluid pressure wave amplitude at wellhead with the inner diameter of drill string表 5 井口钻井液压力波幅值随钻柱内径变化仿真参数Table 5. Simulation parameters for variation of drilling fluid pressure wave amplitude at welhead with inner diameter of drill string密度ρ/(kg·m−3) 动力黏度η/(Pa·s) 压力波频率f/Hz 钻柱内径d/mm 传输距离x/m 1 340 0.060 3 5 46.1，70.2，100.5，112.0，121.4，149.9 4 430 4 结 论
a. 针对高频钻井液压力波衰减问题，基于二维轴对称瞬态流动理论，构建了衰减模型，得出了衰减规律及适用条件。
b. 该模型可准确描述高频钻井液压力波衰减特性。在钻井液压力波频率为5 Hz，钻柱内径为112 mm，钻井液密度为1 340 kg/m3，黏度为0.060 3 Pa·s，压力波传输距离为1 000 m的条件下，理论与实验结果的偏差为3.12%。
c. 高频钻井液压力波幅值衰减量随频率、传输距离及钻井液黏度的增加近似呈指数增大，随钻井液密度及钻柱内径增加逐渐减小，且幅值衰减受频率影响最大。通过统计仿真结果，高频钻井液压力波幅值衰减量随频率的变化率最大为0.126 2 MPa/Hz，随压力波传输距离的变化率最大为3.802 3×10−4 MPa/m，随钻井液黏度的变化率最大为0.009 MPa/(Pa·s)，随钻井液密度的变化率最大为1.386 7×10−4 MPa/(kg·m−3)。本文研究成果可为下一步研究钻井液压力波频率优选提供理论支撑。
-
![]()
图 3 直接顶−基本顶断裂力学计算模型
Fig. 3 Direct roof-basic roof fracture mechanics calculation model
![]()
图 5 基本顶周期来压步距与裂缝深度比关系曲线
Fig. 5 Relationship curves between basic roof periodic weighting step and crack depth ratio
![]()
图 6 基本顶周期来压步距与断裂韧度关系曲线
Fig. 6 Relationship curves between basic roof periodic weighting step and fracture toughness
![]()
图 7 基本顶周期来压步距与直接顶弹性模量关系曲线
Fig. 7 Relationship curves between periodic weighting step of basic roof and elastic modulus of direct roof
![]()
图 8 基本顶周期来压步距与直接顶厚度关系曲线
Fig. 8 Relationship curves between periodic weighting step of basic roof and thickness of direct roof
-
[1] 钱鸣高, 石平五, 许家林. 矿山压力与岩层控制[M]. 徐州: 中国矿业大学出版社, 2010. [2] 宋振骐. 实用矿山压力控制[M]. 徐州: 中国矿业大学出版社, 1988. [3] 钱鸣高,缪协兴,许家林. 岩层控制中的关键层理论研究[J]. 煤炭学报,1996,21(3):225−230. DOI: 10.3321/j.issn:0253-9993.1996.03.001 QIAN Minggao,MIAO Xiexing,XU Jialin. Theoretical study of key stratum in ground control[J]. Journal of China Coal Society,1996,21(3):225−230. DOI: 10.3321/j.issn:0253-9993.1996.03.001
[4] 宋振骐,蒋宇静,刘建康. “实用矿山压力控制”的理论和模型[J]. 煤炭科技,2017(2):1−10. DOI: 10.3969/j.issn.1008-3731.2017.02.001 SONG Zhenqi,JIANG Yujing,LIU Jiankang. Theory and model of “practical method of mine pressure control”[J]. Coal Science & Technology Magazine,2017(2):1−10. DOI: 10.3969/j.issn.1008-3731.2017.02.001
[5] 郑凯歌,王林涛,李彬刚,等. 坚硬顶板强矿压动力灾害演化机理与超前区域防治技术[J]. 煤田地质与勘探,2022,50(8):62−71. DOI: 10.12363/issn.1001-1986.22.04.0222 ZHENG Kaige,WANG Lintao,LI Bingang,et al. Dynamic disaster evolution mechanism of high mine pressure at hard roof and advance area prevention and control technology[J]. Coal Geology & Exploration,2022,50(8):62−71. DOI: 10.12363/issn.1001-1986.22.04.0222
[6] 李金华,段东,岳鹏举,等. 坚硬顶板强制放顶断裂力学模型研究[J]. 煤田地质与勘探,2018,46(6):128−132. DOI: 10.3969/j.issn.1001-1986.2018.06.018 LI Jinhua,DUAN Dong,YUE Pengju,et al. Study on the fracture mechanics model of forced caving of hard roof[J]. Coal Geology & Exploration,2018,46(6):128−132. DOI: 10.3969/j.issn.1001-1986.2018.06.018
[7] 李金华,陈文晓,苏培莉,等. 深孔预裂强制放顶断裂力学模型研究[J]. 煤田地质与勘探,2020,48(6):217−223. DOI: 10.3969/j.issn.1001-1986.2020.06.029 LI Jinhua,CHEN Wenxiao,SU Peili,et al. Research on the fracture mechanics model of deep hole pre–splitting for forced caving[J]. Coal Geology & Exploration,2020,48(6):217−223. DOI: 10.3969/j.issn.1001-1986.2020.06.029
[8] 题正义,张峰,秦洪岩,等. 基于板壳和断裂力学理论的上覆采空区积水危险性判定技术[J]. 煤田地质与勘探,2019,47(1):138−143. DOI: 10.3969/j.issn.1001-1986.2019.01.021 TI Zhengyi,ZHANG Feng,QIN Hongyan,et al. Risk judgment technology of water accumulation in overlying goaf based on plate shell and fracture mechanics theory[J]. Coal Geology & Exploration,2019,47(1):138−143. DOI: 10.3969/j.issn.1001-1986.2019.01.021
[9] HU Jianhua,LEI Tao,ZHOU Keping,et al. Mechanism on simulation and experiment of pre−crack seam formation in stope roof[J]. Journal of Central South University,2014,21(4):1526−1533. DOI: 10.1007/s11771-014-2093-2
[10] 陈新年,王景春,熊咸玉,等. 煤巷复合顶板结构对其稳定性影响试验[J]. 煤田地质与勘探,2019,47(2):157−161. CHEN Xinnian,WANG Jingchun,XIONG Xianyu,et al. Influence of composite roof structure on the stability of coal roadway[J]. Coal Geology & Exploration,2019,47(2):157−161.
[11] 张杰. 采高对浅埋煤层老顶岩层破断距的影响[J]. 辽宁工程技术大学学报(自然科学版),2009,28(2):161−164. DOI: 10.3969/j.issn.1008-0562.2009.02.001 ZHANG Jie. Influence of mining height of main roof on broken length[J]. Journal of Liaoning Technical University (Natural Science),2009,28(2):161−164. DOI: 10.3969/j.issn.1008-0562.2009.02.001
[12] 谷拴成,李金华,黄荣宾. 采场直接顶对周期来压步距的影响[J]. 矿业安全与环保,2015,42(5):34−37. DOI: 10.3969/j.issn.1008-4495.2015.05.009 GU Shuancheng,LI Jinhua,HUANG Rongbin. Influence of stope immediate roof on periodic weighting distance[J]. Mining Safety & Environmental Protection,2015,42(5):34−37. DOI: 10.3969/j.issn.1008-4495.2015.05.009
[13] 谷拴成,黄荣宾,苏培莉. 直接顶岩层特性对综采工作面周期来压步距的影响[J]. 煤炭技术,2017,36(7):4−6. DOI: 10.13301/j.cnki.ct.2017.07.002 GU Shuancheng,HUANG Rongbin,SU Peili. Influence of characteristics of immediate roof strata on periodic weighting length in fully mechanized coal face[J]. Coal Technology,2017,36(7):4−6. DOI: 10.13301/j.cnki.ct.2017.07.002
[14] 弓培林,靳钟铭. 大采高综采采场顶板控制力学模型研究[J]. 岩石力学与工程学报,2008,27(1):193−198. DOI: 10.3321/j.issn:1000-6915.2008.01.027 GONG Peilin,JIN Zhongming. Mechanical model study on roof control for fully−mechanized coal face with large mining height[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(1):193−198. DOI: 10.3321/j.issn:1000-6915.2008.01.027
[15] 刘长友,万志军,曹胜根. 直接顶岩层力学特性对综放采场煤岩破坏的影响规律[J]. 矿山压力与顶板管理,2002,19(1):64−66. LIU Changyou,WAN Zhijun,CAO Shenggen. Effect of mechanical properties of direct roof strata on the destruction of coal rock in fully mechanized stope[J]. Ground Pressure and Strata Control,2002,19(1):64−66.
[16] FENG Qiang,FU Shenggang,WANG Chengxiang,et al. Analytical solution for fracture of stope roof based on Pasternak Foundation model[J]. Soil Mechanics and Foundation Engineering,2019,56(2):142−150. DOI: 10.1007/s11204-019-09582-x
[17] GONG Tao,XIA Binwei,LU Yiyu,et al. Study on the maximum pressure−causing stratum in longwall mining stope and its mechanics analysis[J]. Arabian Journal of Geosciences,2020,13:566. DOI: 10.1007/s12517-020-05625-y
[18] LUO Zhouquan,XIE Chengyu,JIA Nan,et al. Safe roof thickness and span of stope under complex filling body[J]. Journal of Central South University,2013,20(12):3641−3647. DOI: 10.1007/s11771-013-1891-2
[19] 杨登峰,陈忠辉,孙建伟,等. 大采高长壁工作面顶板垮落的裂纹板力学模型[J]. 东南大学学报(自然科学版),2016,46(增刊1):210−216. YANG Dengfeng,CHEN Zhonghui,SUN Jianwei,et al. Crack plate mechanical model for large mining height and longwall face of roof caving[J]. Journal of Southeast University (Natural Science Edition),2016,46(Sup.1):210−216.
[20] 孙闯,宋业杰. 基于断裂力学的长壁工作面导水裂缝带高度预计[J]. 煤矿开采,2016,21(3):81−84. DOI: 10.13532/j.cnki.cn11-3677/td.2016.03.022 SUN Chuang,SONG Yejie. Predict of diversion fissure zone height of long wall face based on fracture mechanics[J]. Coal Mining Technology,2016,21(3):81−84. DOI: 10.13532/j.cnki.cn11-3677/td.2016.03.022
[21] 唐铁吾,刘大安,崔振东,等. 煤矿顶板致裂水压力的断裂力学评估[J]. 煤炭学报,2020,45(增刊2):727−735. DOI: 10.13225/j.cnki.jccs.2020.0065 TANG Tiewu,LIU Da’an,CUI Zhendong,et al. Initiation pressure evaluation of coal mine roof hydraulic fracturing based on fracture mechanics[J]. Journal of China Coal Society,2020,45(Sup.2):727−735. DOI: 10.13225/j.cnki.jccs.2020.0065
[22] 王进学,王家臣,陈忠辉. “两硬”浅埋深厚煤层顶煤顶板运移规律研究[J]. 采矿与安全工程学报,2006,23(2):228−232. DOI: 10.3969/j.issn.1673-3363.2006.02.023 WANG Jinxue,WANG Jiachen,CHEN Zhonghui. Movement rule of shallowly–buried thick coal seams with hard top coal and roof[J]. Journal of Mining & Safety Engineering,2006,23(2):228−232. DOI: 10.3969/j.issn.1673-3363.2006.02.023
[23] 中国航空研究院. 应力强度因子手册[M]. 北京: 科学出版社, 1981. -
期刊类型引用(2)
1. 文国军，黄子恒，王玉丹，史垚城，姜宇昊. 基于仿真数据驱动的激光钻进气体喷嘴结构优化. 钻探工程. 2024(03): 69-75 . 
百度学术
2. 刘旭堂，黄梦婕，王伟. 机械式激光窗口结构设计与防尘罩抗风载能力研究. 四川轻化工大学学报(自然科学版). 2022(01): 59-66 . 百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 185
- HTML全文浏览量: 8
- PDF下载量: 22
- 被引次数: 2
