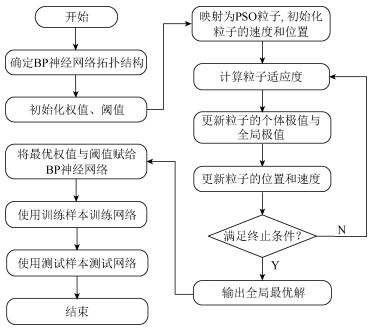
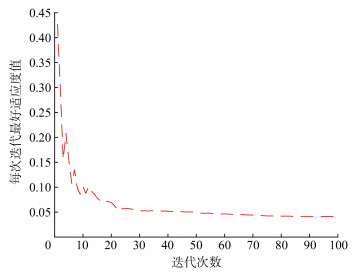
Prediction of the height of water flowing fractured zone based on PSO-BP neural network
-
摘要: 导水裂隙带高度是西部矿区保水采煤的理论依据和关键参数。近年来,BP神经网络广泛应用于导水裂隙带高度预测,但BP神经网络存在收敛速度慢、易陷入局部极小等问题。为提高导水裂隙带高度预测的准确性,利用粒子群优化算法(PSO)对BP神经网络的权值和阈值进行优化,建立基于PSO-BP神经网络的导水裂隙带高度预测模型。选择开采厚度、开采深度、工作面倾斜长度、煤层倾角、覆岩结构特征为导水裂隙带高度主要影响因素,选取22例导水裂隙带高度实测数据对PSO-BP神经网络进行训练,将训练后的PSO-BP神经网络对2例测试样本的预测结果与实际值进行对比,并与BP神经网络预测模型及经验公式预测结果进行对比。结果表明:PSO-BP神经网络预测模型的平均相对误差为1.55%;BP神经网络预测模型的平均相对误差为4.8%,经验公式的最小相对误差为9.4%,PSO-BP神经网络预测精度明显优于BP神经网络和经验公式,且绝对误差和相对误差变化较稳定,可以有效预测导水裂隙带高度。Abstract: The height of water flowing fractured zone is the theoretical basis and key parameter of water-preserved mining in western mining areas of China. In recent years, BP neural network has been widely used to predict the height of water flowing fracture zone, but it has such defects as slow convergence speed and a tendency to fall into local minimum. In order to improve the prediction accuracy of the height of water flowing fractured zone, the weight values and thresholds of BP neural network were optimized by particle swarm optimization(PSO), and a prediction model was established based on PSO-BP neural network. Mining thickness, mining depth, inclined length of working face, dip angle of coal seam, overburden structural characteristics were chosen as the main influential factors of the height of water flowing fractured zone, and 22 measured data of the height of water flowing fractured zone were selected to train PSO-BP neural network. Then the trained PSO-BP neural network was used to predict two test samples, and the results were compared with the actual values, and with the predicting results of BP neural network prediction model and empirical formulas. The research results show that the average relative error of PSO-BP neural network prediction model is 1.55%, and that of BP neural network prediction model and the minimum relative error of empirical formulas are 4.8% and 9.4% respectively. The prediction accuracy of PSO-BP neural network is obviously significantly better than BP neural network and empirical formulas, and the variation of its absolute error and relative error are relatively stable, so PSO-BP neural network can effectively predict the height of water flowing fractured zone.
-
在河堤工程施工中,由于受河水侵蚀作用,土体承载能力低、含水量较高,处于软塑到流塑状态之间,易出现土体不均匀沉降、渗水效果差等目前亟待解决的问题[1]。传统的固堤方法有压力灌浆固堤、高压旋喷桩固堤、地下截渗墙固堤等[2-3]。
低压充填式灌浆固堤方法的孔压一般在49~95 kN/m2,孔压上限为147 kN/m2,需对堤内较大洞穴处重复灌浆3~4次,确保灌实率达96%以上。研究发现,采用低压充填式灌浆可灌注密实土石接合边界,且注浆液沿缝隙运移可至数十米。但该种低压充填式灌浆的方法很难使堤内松土层灌注密实,若松土层较厚,则该法对土体强度的提升有限。高压旋喷桩技术需要协助速度冷凝液、跳喷及喷射液的再灌溉等措施,以防喷射过程中出现堤基附加变形和基础脱空现象,其施工流程繁琐,经济性低,且施工过程中必须加强对既有建筑物的实时监控。相关工程实例表明,在渗水严重、渗透变形大的堤段,采用黏土置换并修筑地下连续截渗墙进行加固效果显著;但其施工技术复杂,造价昂贵。
随着城市地下空间规模的不断发展,人工冷冻技术[4-9]在隧道建设中的应用愈加成熟,在港珠澳大桥拱北隧道应用的管幕冻结法[10-11]的基础上,通过对结构进行优化而衍生出新型的管幕冻结法,大大提高了结构配置的多样性。其实质是利用制冷系统,使土中水结冰变为冻土,形成一道以管幕钢管、冻土组成的止水帷幕,短暂改变岩土的性质使土壤冻结,提高其强度和稳定性。将此法应用到河堤工程中,其形成的冻土帷幕能有效防止水的渗入,当汛期水位上升时,使河堤能抵抗河水对土体的侵蚀,保障河堤工程安全,且施工流程简单,经济性高。胡向东等[12]在拱北隧道暗挖段管幕冻结工法的背景下,通过对2种特殊布置形式进行简化,提出单圈冻结管错位布置冻结模型,应用ANSYS软件对3个特殊位置截面进行温度场数值模拟分析,并验证了在该冻结管错位布置的新型布置形式下,各位置的温度均远低于冻结温度,能有效防止管间水的渗透。吴雨薇等[13]通过在观察路径上布置观测点,开展导热率、原始地温、比热容和潜热4个参数对温度场影响的敏感性研究,分析各因素对温度场的影响效果。胡俊等[14-15]通过对新型管幕冻结法不同冻结管排布方式和管幕钢管的填充形式展开温度场分析,得出2根冻结管沿相邻管幕钢管中心弧线水平布置时,其降温速率及冻结效果均优于2根冻结管沿底面中心径向与钢管内外边界形成的圆相切布置;当管幕钢管中未填充混凝土时,冻结前期温度下降较快,而全部填充混凝土时,冻结后期温度下降较快;间隔填充混凝土与未填充混凝土的方式降温规律基本一致。国内外学者大多基于管幕冻结法在隧道工程建设中的应用进行研究,而较少关注其用于河堤工程建设,笔者利用有限元软件基于温度场对新型管幕冻结法在防渗固堤中的应用展开研究,设置4条分析路径,分析冻土帷幕的基本情况和各路径上的冻结效果特征,以期为今后新型管幕冻结法在防渗固堤工程中的应用及相关研究提供参考。
1 河堤冻土帷幕温度场数值模型的建立
1.1 新型管幕冻结法结构特征
本文研究的新型管幕冻结法[16]形成的支护结构主要由管幕钢管和钢管之间的冻土帷幕组成,如图1所示。相较于拱北隧道采用的管幕冻结法,提出将冻结管配置在相邻管幕钢管之间,而非内部,使结构配置的多样性大幅提高。在利用人工冷冻技术冻结后形成的冻土帷幕和管幕钢管构建一体的受力系统,可以有效抵抗洪水侵蚀,保障工程安全。
1.2 数值计算假定
不同性质土层、地面附着物、地面湿度、降水量和地形等因素均能影响土体温度的变化,当地汛期一般为6—10月,参考文献[17]可知,地表温度夏季为27.8℃,秋季为9.6℃;距地面20 cm深处,夏季温度为23.9℃,秋季为12.2℃,两时间段温度变化规律相反,而本文研究的受冻结影响的土体深度范围远大于20 cm,故推测研究区河堤土温均值约为20℃,因此,本文在不影响结论的基础上,做以下假定[13,18]:
① 模型内土体均质连续,初始温度为18℃;
② 冻结区域外的土体温度恒定;
③ 温度达到–1℃时土体开始冻结,−10℃为最不利条件(即考虑各种不利因素)下的最低冻结温度;
④ 随着温度变化,冻土和未冻土比热容和导热系数不变;
⑤ 不考虑水与坡面土之间的热传递。
1.3 计算模型及路径设置
本文依据兰州市西新线河堤加固工程建立基于河堤坡度i=1∶0.25,长20.0 m、高5.7 m的三维温度场数值模型[19],管幕钢管采用直径为800 mm的空心钢管,为避免钢管暴露在空气中,将钢管放置于0.5 m深处,即钢管顶部距离坡面垂直距离为0.1 m,相邻管幕钢管间布置 2 根直径为127 mm的冻结管,相邻冻结管之间距离为800 mm,冻结管距相邻管幕钢管200 mm,采用边划分网格的方式,划分后模型如图2所示。
如图2所示,本文各路径均设置于坡面中垂面,为研究坡面各点的冻结加固情况设置路径1,从左侧管幕钢管正上方坡面为起点至右侧管幕钢管正上方坡面,每隔0.2 m设置1个观测点,共设置11个;为研究冻结温度随土体深度的变化情况设置路径2,以管幕钢管中心连线中垂线与坡面交点为起点,每隔0.1 m设置1个观测点,共设置11个;为研究冻结过程中钢管边界温度的变化设置路径3,以管幕钢管中心连线与钢管边界交点为起点,沿逆时针方向每隔15°设置1个观测点,共设置7个;为研究土体传热的影响及管幕布设范围内是否冻结密实设置路径4,以钢管中心连线为对称轴,与路径1呈对称设置。
1.4 参数选取
参考相关文献及报告[19-20],从土层成因和结构特征的角度进行分析,认为该类型土与砂质粉土性质相近,故本文研究对象为砂质粉土。结合本课题组相关研究成果[4,13-14],设计盐水冻结方案为:积极冻结24 h后盐水温度将降至0℃,冻结120 h后盐水温度降至–15℃,冻结240 h后盐水温度降至–28℃,维护冻结期盐水温度为–28℃。
表 1 土体材料参数取值Table 1. Material parameters of soils密度/
(kg·m−3)导热系数/
(kJ·m−1·d−1·℃−1)比热容/
(kJ·kg−1·℃−1)相变潜热/
(103 kJ·m−3)未冻土 冻土 未冻土 冻土 1 857 124 152 1.736 1.35 1.04 表 2 盐水冻结方案Table 2. Freezing plan of brine时间/h 温度/℃ 时间/h 温度/℃ 0 18 360 −28 24 0 480 −28 120 −15 720 −28 240 −28 960 −28 1.5 热分析基本理论
热分析遵循能量守恒定律,即在一个封闭系统中(没有能量的流入或流出),有:
$$ Q-W = \Delta U + \Delta K_{{\rm{E}}} + \Delta P_{{\rm{E}}} $$ (1) 式中:Q为热量;W为做功;ΔU为系统内能;ΔKE为系统动能;ΔPE为系统势能。
3种基本的传热形式为:热传导、热对流及热辐射。无内热源的非稳态三维传热过程遵循如下能量控制方程[21]:
$$ \frac{{\partial} }{{\partial x}}\left( {k\frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {k\frac{{\partial T}}{{\partial y}}} \right) + \frac{\partial }{{\partial {\textit{z}}}}\left( {k\frac{{\partial T}}{{\partial {\textit{z}}}}} \right) = \rho 'C\frac{{\partial T}}{{\partial t}} $$ (2) 式中:T为温度;t为时间;ρ'为材料密度;C为比热容;k为导热系数。
可根据以下3种形式[21]的边界条件求出具体的温度场分布。
物体边界上温度函数为:
$$ \left. T \right|_{\varGamma } = f\left( {x,y, {\textit{z}},t} \right) $$ (3) 物体边界上热流密度函数为:
$$ - k\frac{{\partial T}}{{\partial n}}\left|_ \varGamma \right. = g\left( {x,y, {\textit{z}},t} \right) $$ (4) 与物体接触的流体介质的温度和对流换热系数为:
$$ - k\frac{{\partial T}}{{\partial n}}\left|_ \varGamma \right. = \alpha \left( {T - T_{\rm{f}}} \right)\left|_ \varGamma \right. $$ (5) 式中:Γ为物体边界;f (x, y, z, t)为已知温度函数;g(x, y, z, t)为热流密度函数;α为对流换热系数;Tf 为流体介质温度。
土体的冻结过程是相变导热过程,相变导热问题(Stefan问题)[22]需要考虑相变潜热(相变过程吸收或释放的热量)。土体冻结时释放的结冰潜热与土体的未冻含水量的关系为:
$$ \sigma_ {\rm{n}} = \left( {w-w_{\text{u}}} \right)\gamma_ {\rm{s}}L $$ (6) 式中:σn 为土体结冰潜热;w为融土含水量;wu为冻土中未冻含水量;γs为融土容重;L为水结冰时释放的相变潜热[23]。
带相变瞬态温度场问题的热平衡控制微分方程[24]如下:
$$ C_{\rm{f}}\frac{{\partial T_{\rm{f}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {k_{\rm{f}}\frac{{\partial T_{\rm{f}}}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {k_{\rm{f}}\frac{{\partial T_{\rm{f}}}}{{\partial y}}} \right) + \frac{\partial }{{\partial {\textit{z}}}}\left( {k_{\rm{f}}\frac{{\partial T_{\rm{f}}}}{{\partial {\textit{z}}}}} \right) $$ (7) 在未冻区Ωu内:
$$ C_{\rm{u}}\frac{{\partial T_{\rm{u}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {k_{\rm{u}}\frac{{\partial T_{\rm{u}}}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {k_{\rm{u}}\frac{{\partial T_{\rm{u}}}}{{\partial y}}} \right) + \frac{\partial }{{\partial {\textit{z}}}}\left( {k_{\rm{u}}\frac{{\partial T_{\rm{u}}}}{{\partial {\textit{z}}}}} \right) $$ (8) 式中:下标f,u分别为冻、融状态;Tu为未冻区介质温度。
土体的导热系数和比热容会随温度而发生变化,两相界面的位置也随之变化,所以在界面处的能量守恒条件为非线性,可运用数值模拟方法获得数值解。
2 冻土帷幕基本情况
图3为1—1剖面冻结过程中冻土帷幕发展情况及温度(−1、−10℃)等值线图。观察发现:冻土帷幕随冻结过程进行自冻结管向周围扩展,−1、−10℃等温线分别于冻结进行120、192 h时与钢管边界发生交圈,于264、360 h与坡面发生交圈,−1、−10℃等温线分别于冻结进行216、312 h时在相邻冻结管之间发生交圈,在0.5 m深度范围内,钢管上侧土体受冻结影响最小,于冻结进行336、432 h时−1、−10℃等温线才发生交圈;而在0.5 m深度以下,受土体传热影响其冻结效果和冻结范围远远小于另一侧,在整个冻结过程完成后,钢管下侧−10℃等温线甚至未发生交圈。
总体上,在整个冻结过程中,冻土帷幕自冻结管处形成后向周围蔓延,不论在0.5 m深度哪一侧,在冻结前8 d,其冻土帷幕的发展速率并无太大差别。在第8天后,上侧的冻土帷幕开始出现“加速”现象,相较于另一侧冻土帷幕,其发展更快、强度更高,冻结更密实。此时,在距离冻结管较远的钢管上部是上侧最后形成冻土帷幕的区域。
3 不同路径冻结模拟结果分析
路径1上冻结情况如图4所示。在路径1上各观测点在冻结完成后温度相差不大,均降至−24℃以下,坡面冻结均匀密实。距中垂线0.6 m位置处最低温为−25.34℃,中垂线位置为最高温−24.50℃,观察图4b发现,最终冻结温度呈现出“M”形特征,距中垂线0.4 m处的观测点降温速率最快,在冻结进行约264 h,温度便降至−1℃以下;而越靠近管幕钢管,降温速率越慢,钢管正上方的观测点在冻结进行约336 h时,才降至冻结温度。
路径2上冻结情况如图5所示。冻结完成后,在路径2上各观测点温度差异较大,距离坡面越近,降温速率越快,土体温度也越低,最低、最高温分别为−24.50、−8.52℃,但各点之间并不构成线性关系,坡面近端相邻两观测点之间温差为0.06℃,而远端温差为2.87℃。同时注意到,在17号观测点两侧同样距离处的12号、22号观测点与该点(17号观测点)温度差分别为−3、13℃,可见1 m深度以下土体的传热对温度场影响很大。
路径3上冻结情况如图6所示。观察图6发现,在整个冻结过程完成后,路径3上观测点最低、最高温分别为−24.94、−2.89℃,相差约22℃,离冻结管越近则降温速率越快(平均1.07℃/d)、冻结效果越好,反之则速率慢(平均0.52℃/d)、效果差。最不利条件下冻结范围(最小冻结范围)在26号观测点附近,距离坡面约0.78 m。
路径4上冻结情况如图7所示。相较于路径1,在1 m深度以下的土体传热影响下,路径4上各观测点的降温速率和冻结效果显著下降,直至冻结456 h后才有观测点降至−1℃以下,且在整个冻结过程完成后,各点温度均在−10℃以上,路径上观测点最大温差约为6℃,冻土壁均匀性较差。路径上最终平均冻结温度约为−6℃,即在1 m深度以下的土体影响下,冻结效果削弱了约18℃。
就冻结管而言,其表面各位置处吸热能力是相同的,若冻结管两侧土层厚度一致,其两侧土体冻结效果应无显著区别。而本文中两侧土层厚度并不一致,这便导致在冻结过程中1 m深度两侧土层之间形成温差,下侧土层向上侧土层放热,进而造成冻结管两侧土体冻结效果差异显著。
4 指导或建议
在河堤实施管幕冻结法后,堤面最快可在第11天开始出现冻土,第14天冻土覆盖整个堤面,且在冻结完成后,整个堤面可降至−24℃以下。土体最终冻结温度与深度之间并非呈简单线性函数关系,而是更接近于指数函数关系。随着深度的增加,冻结加固效果逐渐削弱,但至少可保证堤面和0.78 m深度范围内的土体冻结密实。
故将新型管幕冻结法用于河堤工程中,可使河堤一定深度范围内形成一道承载能力高、密封性好、止水性能优的冻土帷幕,使堤面抵抗河水侵蚀能力大大提高,且其施工流程简单,施工效率高,经济性好。因此,将该法用于河堤加固是切实可行的。
5 结 论
a. 冻土帷幕随冻结过程的进行自冻结管向周围扩展,在钢管靠土体一侧,受土体影响其冻结效果和冻结范围远远小于坡面侧,在整个冻结过程完成后,钢管下侧冻土帷幕较上侧均匀性较差;坡面冻结均匀密实,坡面上各观测点温度均在−24℃以下,距中垂线0.6 m位置处最低温为−25.34℃,中垂线位置最高温为−24.50℃,最终冻结温度和降温速率均呈现出“M”形特征。
b. 冻结前8 d,冻结管两侧冻土帷幕的发展速率并无太大差别。在第8天后,靠坡面侧的冻土帷幕开始出现“加速”现象,相较于另一侧冻土帷幕,其发展更快、强度更高、冻结更密实。
c. 在整个冻结过程完成后,路径3上观测点最低、最高温分别为−24.94、−2.89℃,相差约22℃,最不利条件(即考虑各种不利因素)下冻结范围(最小冻结范围)在26 号观测点附近,距离坡面约0.78 m。
d. 将新型管幕冻结法用于河堤工程中,可使河堤一定深度范围内形成一道承载能力高、密封性好、止水性能优的冻土帷幕,使堤面抵抗河水侵蚀的能力大大提高,且其施工流程简单,施工效率高,经济性好。
-
表 1 导水裂隙带高度实测样本数据
Table 1 Measured sampling data of the height of water flowing fractured zone
编号 工作面 开采厚度/m 开采深度/m 工作面倾斜长度/m 煤层倾角/(°) 覆岩结构特征 导水裂隙带高度/m 1 北皂煤矿H2101 3.6 359 150 2.3 软弱–软弱 30.0 2 济宁三号煤矿1301 6.3 480 170 4.0 软弱–坚硬 68.6 3 钱家营煤矿1672东 3.0 484 143 17.0 坚硬–软弱 40.0 4 东欢坨煤矿2186 3.7 360 70 23.0 坚硬–软弱 56.8 5 林南仓煤矿1221 4.0 232 71 8.0 坚硬–软弱 33.0 6 鲍店煤矿1303 8.7 435 153 8.0 坚硬–坚硬 71.0 7 鲍店煤矿1316 8.6 357 169 6.5 坚硬–软弱 65.5 8 南屯煤矿63上10 5.8 368 125 6.0 坚硬–坚硬 70.7 9 兴隆庄煤矿4320 8.0 450 170 8.0 坚硬–软弱 86.8 10 兴隆庄煤矿1301 6.4 414 193 9.0 坚硬–软弱 72.9 11 新集一矿1303 7.8 329 134 8.0 软弱–坚硬 83.9 12 杨村煤矿301 6.4 270 120 11.5 坚硬–软弱 62.0 13 协鑫煤矿1703-1 9.6 302 120 7.0 软弱–软弱 112.0 14 北皂煤矿H2106 4.1 330 150 7.0 软弱–软弱 38.8 15 下沟煤矿ZF2801 9.9 332 93 2.0 软弱–坚硬 125.8 16 潘一煤矿2622(3) 5.8 553 180 8.0 软弱–软弱 65.3 17 百善煤矿664 3.0 168 137 5.5 软弱–软弱 27.8 18 南屯93上01 5.3 542 175 15.0 坚硬–坚硬 67.5 19 王庄煤矿6206 5.9 296 148 4.5 坚硬–坚硬 114.7 20 梁家煤矿1206 4.0 350 136 9.0 软弱–软弱 35.0 21 杨庄煤矿8煤层 1.7 320 65 6.0 坚硬–软弱 27.5 22 某矿3煤层 6.5 263 180 4.0 坚硬–坚硬 83.9 23 兴隆庄煤矿5306 7.1 412 160 9.5 坚硬–软弱 74.4 24 鲍店煤矿1310 8.7 409 198 6.0 坚硬–软弱 83.0 表 2 PSO-BP神经网络、BP神经网络及经验公式预测结果
Table 2 Predicting results of PSO-BP neural network, BP neural network and empirical formulas
编号 导水裂隙带高度/m 绝对误差/m 相对误差/% PSO-BP BP 式(6) 式(7) PSO-BP BP 式(6) 式(7) PSO-BP BP 式(6) 式(7) 23 75.3 78.6 81.4~102.2 152.0 0.9 4.2 7.0~27.8 77.6 1.2 5.6 9.4~37.4 104.3 24 81.4 86.3 97.0~117.8 184.0 1.6 3.3 14.0~34.8 101.0 1.9 4.0 16.9~41.9 121.7 -
[1] 范立民, 马雄德, 蒋泽泉, 等. 保水采煤研究30年回顾与展望[J]. 煤炭科学技术, 2019, 47(7): 1-30. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201907001.htm FAN Limin, MA Xiongde, JIANG Zequan, et al. Review and thirty years prospect of research on water-preserved coal mining[J]. Coal Science and Technology, 2019, 47(7): 1-30. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201907001.htm
[2] 徐智敏, 高尚, 崔思源, 等. 哈密煤田生态脆弱区保水采煤的水文地质基础与实践[J]. 煤炭学报, 2017, 42(1): 80-87. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201701011.htm XU Zhimin, GAO Shang, CUI Siyuan, et al. Hydro-geological basic and practice for water-preserved mining in ecologically vulnerable area: A case study in Hami coalfield[J]. Journal of China Coal Society, 2017, 42(1): 80-87. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201701011.htm
[3] 范立民. 保水采煤面临的科学问题[J]. 煤炭学报, 2019, 44(3): 667-674. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201903002.htm FAN Limin. Some scientific issues in water-preserved coal mining[J]. Journal of China Coal Society, 2019, 44(3): 667-674. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201903002.htm
[4] 娄高中, 郭文兵, 高金龙. 基于量纲分析的非充分采动导水裂缝带高度预测[J]. 煤田地质与勘探, 2019, 47(3): 147-153. DOI: 10.3969/j.issn.1001-1986.2019.03.023 LOU Gaozhong, GUO Wenbing, GAO Jinlong. Prediction of the height of water flowing fractured zone under subcritical mining based on dimensional analysis[J]. Coal Geology & Exploration, 2019, 47(3): 147-153. DOI: 10.3969/j.issn.1001-1986.2019.03.023
[5] 国家安全监管总局, 国家煤矿安监局, 国家能源局, 等. 建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范[M]. 北京: 煤炭工业出版社, 2017. State Administration of Work Safety, National Coal Mine Safety Administration, National Energy Administration, et al. Specifications for coal pillar retention and compressed coal mining in buildings, water bodies, railways and main shafts[M]. Beijing: China Coal Industry Publishing House, 2017.
[6] 许家林, 朱卫兵, 王晓振. 基于关键层位置的导水裂隙带高度预计方法[J]. 煤炭学报, 2012, 37(5): 762-769. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201205011.htm XU Jialin, ZHU Weibing, WANG Xiaozhen. New method to predict the height of fractured water-conducting zone by location of key strata[J]. Journal of China Coal Society, 2012, 37(5): 762-769. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201205011.htm
[7] 施龙青, 辛恒奇, 翟培合, 等. 大采深条件下导水裂隙带高度计算研究[J]. 中国矿业大学学报, 2012, 41(1): 37-41. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201201008.htm SHI Longqing, XIN Hengqi, ZHAI Peihe, et al. Calculating the height of water flowing fracture zone in deep mining[J]. Journal of China University of Mining & Technology, 2012, 41(1): 37-41. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201201008.htm
[8] 徐智敏, 孙亚军, 高尚, 等. 干旱矿区采动顶板导水裂隙的演化规律及保水采煤意义[J]. 煤炭学报, 2019, 44(3): 767-776. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201903013.htm XU Zhimin, SUN Yajun, GAO Shang, et al. Law of mining induced water conduction fissure in arid mining area and its significance in water-preserved coal mining[J]. Journal of China Coal Society, 2019, 44(3): 767-776. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201903013.htm
[9] 李超峰, 虎维岳, 王云宏, 等. 煤层顶板导水裂缝带高度综合探查技术[J]. 煤田地质与勘探, 2018, 46(1): 101-107. DOI: 10.3969/j.issn.1001-1986.2018.01.018 LI Chaofeng, HU Weiyue, WANG Yunhong, et al. Comprehensive detection technique for coal seam roof water flowing fractured zone height[J]. Coal Geology & Exploration, 2018, 46(1): 101-107. DOI: 10.3969/j.issn.1001-1986.2018.01.018
[10] 郭文兵, 娄高中, 赵保才. 芦沟煤矿软硬交互覆岩放顶煤开采导水裂缝带高度研究[J]. 采矿与安全工程学报, 2019, 36(3): 519-526. https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL201903012.htm GUO Wenbing, LOU Gaozhong, ZHAO Baocai. Study on the height of water-conductive fracture zone in alternate overburden of soft and hard with top coal caving mining in Lugou coal mine[J]. Journal of Mining & Safety Engineering, 2019, 36(3): 519-526. https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL201903012.htm
[11] 李振华, 许延春, 李龙飞, 等. 基于BP神经网络的导水裂隙带高度预测[J]. 采矿与安全工程学报, 2015, 32(6): 905-910. https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL201506007.htm LI Zhenhua, XU Yanchun, LI Longfei, et al. Forecast of the height of water flowing fractured zone based on BP neural networks[J]. Journal of Mining & Safety Engineering, 2015, 32(6): 905-910. https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL201506007.htm
[12] 施龙青, 黄纪云, 韩进, 等. 导水裂隙带高度预测的PCA-BP模型[J]. 中国科技论文, 2019, 14(5): 471-475. DOI: 10.3969/j.issn.2095-2783.2019.05.001 SHI Longqing, HUANG Jiyun, HAN Jin, et al. PCA-BP model for height prediction of water conducting fracture zone[J]. China Science paper, 2019, 14(5): 471-475. DOI: 10.3969/j.issn.2095-2783.2019.05.001
[13] 邵良杉, 马寒. 煤体瓦斯渗透率的PSO-LSSVM预测模型[J]. 煤田地质与勘探, 2015, 43(4): 23-26. DOI: 10.3969/j.issn.1001-1986.2015.04.005 SHAO Liangshan, MA Han. Model of coal gas permeability prediction based on PSO-LSSVM[J]. Coal Geology & Exploration, 2015, 43(4): 23-26. DOI: 10.3969/j.issn.1001-1986.2015.04.005
[14] 毛志勇, 黄春娟, 路世昌, 等. 基于APSO-WLS-SVM的含瓦斯煤渗透率预测模型[J]. 煤田地质与勘探, 2019, 47(2): 66-71. DOI: 10.3969/j.issn.1001-1986.2019.02.011 MAO Zhiyong, HUANG Chunjuan, LU Shichang, et al. Model of gas-bearing permeability prediction based on APSO- WLS-SVM[J]. Coal Geology & Exploration, 2019, 47(2): 66-71. DOI: 10.3969/j.issn.1001-1986.2019.02.011
[15] 温正, 孙华克. MATLAB智能算法[M]. 北京: 清华大学出版社, 2017. WEN Zheng, SUN Huake. MATLAB smart algorithm[M]. Beijing: Tsinghua University Press, 2017.
[16] 吕伟才, 黄晖, 池深深, 等. 概率积分预计参数的神经网络优化算法[J]. 测绘科学, 2019, 44(9): 35-41. https://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201909006.htm LYU Weicai, HUANG Hui, CHI Shenshen, et al. Neural network optimization algorithm for the prediction parameters of probability integral method[J]. Science of Surveying and Mapping, 2019, 44(9): 35-41. https://www.cnki.com.cn/Article/CJFDTOTAL-CHKD201909006.htm
[17] 钱锋. 粒子群算法及其工业应用[M]. 北京: 科学出版社, 2013. QIAN Feng. Particle swarm algorithm and its industrial application[M]. Beijing: Science Press, 2013.
[18] 王雨虹, 刘璐璐, 付华, 等. 基于改进BP神经网络的煤矿冲击地压预测方法研究[J]. 煤炭科学技术, 2017, 45(10): 36-40. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201710006.htm WANG Yuhong, LIU Lulu, FU Hua, et al. Study on predicted method of mine pressure bump based on improved BP neural network[J]. Coal Science and Technology, 2017, 45(10): 36-40. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201710006.htm
[19] 王晓振, 许家林, 韩红凯, 等. 顶板导水裂隙高度随采厚的台阶式发育特征[J]. 煤炭学报, 2019, 44(12): 3740-3749. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201912015.htm WANG Xiaozhen, XU Jialin, HAN Hongkai, et al. Stepped development characteristic of water flowing fracture height with variation of mining thickness[J]. Journal of China Coal Society, 2019, 44(12): 3740-3749. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201912015.htm
[20] 郭文兵, 娄高中. 覆岩破坏充分采动程度定义及判别方法[J]. 煤炭学报, 2019, 44(3): 755-766. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201903012.htm GUO Wenbing, LOU Gaozhong. Definition and distinguishing method of critical mining degree of overburden failure[J]. Journal of China Coal Society, 2019, 44(3): 755-766. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201903012.htm
[21] 尹尚先, 徐斌, 徐慧, 等. 综采条件下煤层顶板导水裂缝带高度计算研究[J]. 煤炭科学技术, 2013, 41(9): 138-142. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201309031.htm YIN Shangxian, XU Bin, XU Hui, et al. Study on height calculation of water conducted fractured zone caused by fully mechanized mining[J]. Coal Science and Technology, 2013, 41(9): 138-142. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201309031.htm
[22] 胡炳南, 张华兴, 申宝宏. 建筑物、水体、铁路及主要井巷煤柱留设与压煤开采指南[M]. 北京: 煤炭工业出版社, 2017. HU Bingnan, ZHANG Huaxing, SHEN Baohong. Guidelines for coal pillar retention and compressed coal mining in buildings, water bodies, railways and main shafts[M]. Beijing: China Coal Industry Publishing House, 2017.
[23] 王正帅, 邓喀中, 谭志祥. 导水裂缝带高度预测的模糊支持向量机模型[J]. 地下空间与工程学报, 2011, 7(4): 723-727. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201104018.htm WANG Zhengshuai, DENG Kazhong, TAN Zhixiang. Height prediction of water fractured zone based on fuzzy SVM[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(4): 723-727. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201104018.htm
[24] 樊振丽. 纳林河复合水体下厚煤层安全可采性研究[D]. 北京: 中国矿业大学(北京), 2013. FAN Zhenli. Mining safety research of thick coal seam under aquifers and surface water in Nalinhe mine area[D]. Beijing: China University of Mining and Technology(Beijing), 2013.
[25] 曹博, 白刚, 李辉. 基于PCA-GA-BP神经网络的瓦斯含量预测分析[J]. 中国安全生产科学技术, 2015, 11(5): 84-90. https://www.cnki.com.cn/Article/CJFDTOTAL-LDBK201505016.htm CAO Bo, BAI Gang, LI Hui. Prediction of gas content based on PCA-GA-BP neural network[J]. Journal of Safety Science and Technology, 2015, 11(5): 84-90. https://www.cnki.com.cn/Article/CJFDTOTAL-LDBK201505016.htm
[26] 韩亮, 刘殿书, 李红江, 等. 基于Weibull模型的高台阶抛掷爆破爆堆形态BP神经网络预测[J]. 煤炭学报, 2013, 38(11): 1947-1952. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201311009.htm HAN Liang, LIU Dianshu, LI Hongjiang, et al. BP neural network forecast of blasting muck pile form of high bench cast blasting based on Weibull model[J]. Journal of China Coal Society, 2013, 38(11): 1947-1952. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201311009.htm
[27] 臧子婧, 吴海波, 张平松, 等. 基于ABC-BP模型的煤层含气量预测[J]. 煤田地质与勘探, 2021, 49(2): 152-158. DOI: 10.3969/j.issn.1001-1986.2021.02.019 ZANG Zijing, WU Haibo, ZHANG Pingsong, et al. Prediction of coal seam gas content based on ABC-BP model[J]. Coal Geology & Exploration, 2021, 49(2): 152-158. DOI: 10.3969/j.issn.1001-1986.2021.02.019
[28] 宁永香, 崔希民. 矿山边坡地表变形的PSO-ELM预测模型[J]. 煤田地质与勘探, 2020, 48(6): 201-206. DOI: 10.3969/j.issn.1001-1986.2020.06.027 NING Yongxiang, CUI Ximin. PSO-ELM prediction model for surface deformation of mine slope[J]. Coal Geology & Exploration, 2020, 48(6): 201-206. DOI: 10.3969/j.issn.1001-1986.2020.06.027








 下载:
下载: