Microseismic monitoring and assessment of segmented hydraulic fracturing of horizontal wells in coal seam roofs
-
摘要:背景
微震监测作为一种无损监测技术被广泛用于煤层水力压裂效果评价，但由于建立层状波速模型时缺乏对同层介质中垂向波速梯度的考虑，导致走时计算和震源定位精度有待提高，影响了煤层水力压裂评价的准确性。
目的和方法以安徽某矿煤层分段水力压裂工程为背景，提出了一种基于泛克里金插值法改进的波速模型。结合各向异性因子约束，在声波测井波速模型的基础上，对同层介质中网格波速数值进行插值计算，表征其各向异性特征，并以此修正弹性波传播路径。通过已知位置射孔事件的震源定位精度对比，验证了改进波速模型的有效性。基于该模型，进一步计算了储层渗透率和储层改造体积 (stimulated reservoir volume，SRV)，实现了对煤层水力压裂效果的综合评价。
结果与结论结果表明，泛克里金波速插值相比于线性插值能够有效提升震源定位精度，对于同一射孔点，插值后模型定位误差较初始层状模型最高降低了7.22 m。水力压裂效果评价中，波速插值后的震源定位结果得到改善，微震事件在垂向方向离散性得到有效约束，各压裂段有效影响半径约90 m。煤层区域内微震事件分布密度与渗透率存在差异，各段井筒附近压后渗透率较高。储层改造体积总计为1.977×107 m3，改造体积及水力裂缝长度与注入总液量正相关，基于微震评价的压裂改造效果与预期设计相符。
Abstract:BackgroundMicroseismic monitoring, a non-destructive monitoring technique, has been extensively applied in the hydraulic fracturing performance assessment of coal seams. However, little attention is paid to the vertical wave velocity gradients in media in the same layer during the construction of layered wave velocity models. This leads to limited precision of travel time calculation and microseismic source localization, thus affecting the assessment accuracy of the hydraulic fracturing of coal seams.
Objective and MethodsBased on the coal seam segmented hydraulic fracturing project in a mine in Anhui, this study proposes an improved velocity model based on the Universal Kriging interpolation method. By incorporating anisotropy factors, the velocity values in the grid cells of the same layer are interpolated on the basis of the sonic logging velocity model, to characterize the anisotropic features, which are then used to correct the elastic wave propagation path. The effectiveness of the improved velocity model is validated by comparing the source location accuracy of known perforation events. Based on this model, further calculations of reservoir permeability and Stimulated Reservoir Volume (SRV) were performed, achieving a comprehensive evaluation of the coal seam hydraulic fracturing effect.
Results and ConclusionsThe results indicate that compared to the linear interpolation method, the universal Kriging interpolation method effectively enhanced the microseismic source localization accuracy. For the same perfo-ration point, the localization errors yielded by the improved wave velocity model decreased by up to 7.22 m compared to those of the initial layered wave velocity model. The hydraulic fracturing performance assessment reveals that the microseismic source localization accuracy after wave velocity interpolation was improved and that the vertical discreteness of microseismic events was effectively restricted, with the effective influence radius of various fracturing segments determined at about 90 m. The distribution density of microseismic events and the permeability varied across the coal seam area, with high post-fracturing permeability observed near the wellbore of various fracturing segments. The SRVs in horizontal well No.1 totaled 1.977 × 107 m3, and the SRV and hydraulic fracture length were positively correlated with the total volume of injected fluids. Overall, the hydraulic fracturing performance based on microseismic assessment aligns with the expectation.
-
水力压裂效果评价是优化压裂设计与提高非常规储层开发效率的关键环节[1-3]。微震监测作为一种无损监测技术，能够直观反映煤岩体破裂演化规律，定量评估水力压裂影响范围，已成为煤层等非常规储层开发的重要方法[4-5]。在工程应用中，微震数据的准确解译依赖于波速模型的精度，然而传统单一波速模型假设介质均匀且弹性波沿直线传播，忽略了层状介质的各向异性特征，易引入系统性误差[6-8]。特别是在煤系中，岩体层状赋存特征显著，传统模型难以有效描述复杂波速分布，限制了微震监测的应用效果[9-12]。针对上述问题，已有研究尝试通过引入精细化波速模型改善震源定位精度。陈炳瑞等[13]提出的分层震源定位模型有效提升了定位精度，但该模型的波速值难以收敛于真实值；巩思园等[14]基于P波波速的垂向各向异性，构建了异向波速模型，有效减少地面监测误差；Wang Yi等[15]利用高分辨率波速模型，将定位误差从40 m以上降低至约30 m。此外，Feng Qiang等[16]结合深度强化学习算法，进一步提高了各向异性波速模型的定位精度和计算鲁棒性。然而，这些研究主要聚焦于波速模型的构建，对波速分布连续性和各向异性描述仍有改进空间。在层状介质中，由于各向异性导致弹性波传播路径偏离几何最短路径，而沿最小走时传播[17]。而缺乏对波速各向异性的精确表征会导致传播路径产生偏差，增加走时残差并影响震源定位精度[18-19]。综上所述，在进行微震数据处理时，应对介质波速的各向异性进行表征，以保证数据处理的有效性[20-22]。然而，目前的层状波速模型普遍假设介质各向同性，忽略了波速垂向各向异性对路径和走时计算的影响，限制了微震监测精度及应用效果的提升。在此基础上，泛克里金(universal Kriging)插值法作为一种地质学中参数插值的有效工具，已被证明能够用于改进离散地球物理观测数据的连续性表征[23-24]。但该方法在微震数据处理中的应用鲜有报道，且在有限观测条件下，煤系波速分布垂向各向异性的表征仍不充分。
针对煤层水力压裂微震监测中传统波速模型难以表征层状介质各向异性、导致震源定位误差的问题，笔者以安徽某矿压裂工程为背景，提出一种基于泛克里金插值法改进的波速模型。通过融合泛克里金插值算法与各向异性因子约束，重构层状介质弹性波传播路径计算模型，并基于射孔事件定位验证其精度提升效果。进一步结合储层渗透率分布与改造体积(SRV)的三维量化分析，构建水力压裂效果综合评价体系，旨在为压裂方案动态优化提升提供技术支撑。
1 基本原理
1.1 基于泛克里金插值的同层波速梯度构建
含煤地层的应力波在垂向上存在明显差异，各向异性对称轴与层间界面垂直，是一种具有垂直对称轴的横观各向同性(vertical transverse isotropy, VTI)介质[25]。介质的各向异性参数为：
$$ \left\{ \begin{aligned} & \varepsilon {\text{ = }}\frac{{{c_{11}} - {c_{13}}}}{{2{c_{33}}}} \\ & \delta = \frac{{{{\left( {{c_{13}} + {c_{55}}} \right)}^2} - {{\left( {{c_{33}} - {c_{55}}} \right)}^2}}}{{2{c_{33}}\left( {{c_{33}} - {c_{55}}} \right)}} \\ & \gamma = \frac{{{c_{66}} - {c_{55}}}}{{2{c_{55}}}} \end{aligned} \right. $$ (1) 虽然多数岩体为弱到中各向异性，各向异性因子< 0.6，但在走时计算过程中忽略同一层状中各向异性产生的波速梯度，易造成系统性误差[26]。因此，为进一步表征岩层中垂向波速梯度，以初始层状波速模型为测量值，采用泛克里金插值法在同一层垂直方向均匀插入不同数值的波速分布，将同一层进一步划分为具有波速梯度的岩层，降低各向异性对走时计算的影响。
泛克里金插值法以变异函数理论为基础，对限定区域内变量取值进行无偏最优估计。该方法假设待插值点属性可由临近点属性推导，同时考虑各观测点与待插值点位置相对关系，可有效避免系统误差产生的“屏蔽效应”[27]。相较于线性插值等传统方法，泛克里金插值法能够在综合考虑数据的空间相关性的同时提供预测误差估计值，使插值结果更加平滑且符合实际地质特征。此外，泛克里金法生成的插值误差(克里金方差)可作为量化指标，有效评估插值结果的可靠性。
深度h处波速的泛克里金预测公式为：
$$ \hat Z\left( {{h_0}} \right) = \sum\limits_{i = 1}^n {{\lambda _i}Z\left( {{h_i}} \right)} $$ (2) $$ Z\left( h \right) = m\left( h \right) + r\left( h \right) $$ (3) $$ m\left( h \right) = \sum\limits_{i = 0}^n {{\mu _i}{f^i}\left( h \right)} \left( {{f^0}\left( h \right) = 1} \right) $$ (4) 通过变异函数考察插值点与测量点空间关系，表达式为：
$$ \gamma \left( {\Delta h} \right) = \frac{1}{2}{\text{Var}}\left[ {Z\left( h \right) - Z\left( {h + \Delta h} \right)} \right] $$ (5) 样本变异函数表示为：
$$ \hat \gamma \left( {\Delta h} \right) = \frac{1}{{2{n_{\Delta h}}}}\sum\limits_{i = 1}^{{n_{\Delta h}}} {{{\left[ {Z\left( {{h_i} + \Delta h} \right) - Z\left( {{h_i}} \right)} \right]}^2}} $$ (6) 根据无偏估计原则，观测值与估计值需满足[28]：
$$ E\left[ {Z\left( {{h_0}} \right) - \hat Z\left( {{h_0}} \right)} \right] = \sum\limits_{i = 1}^n {{\lambda _i}} m\left( {{h_i}} \right) - m\left( {{h_0}} \right) = 0 $$ (7) 基于变异函数，泛克里金求解未知权值系数λ和μ公式[29]为：
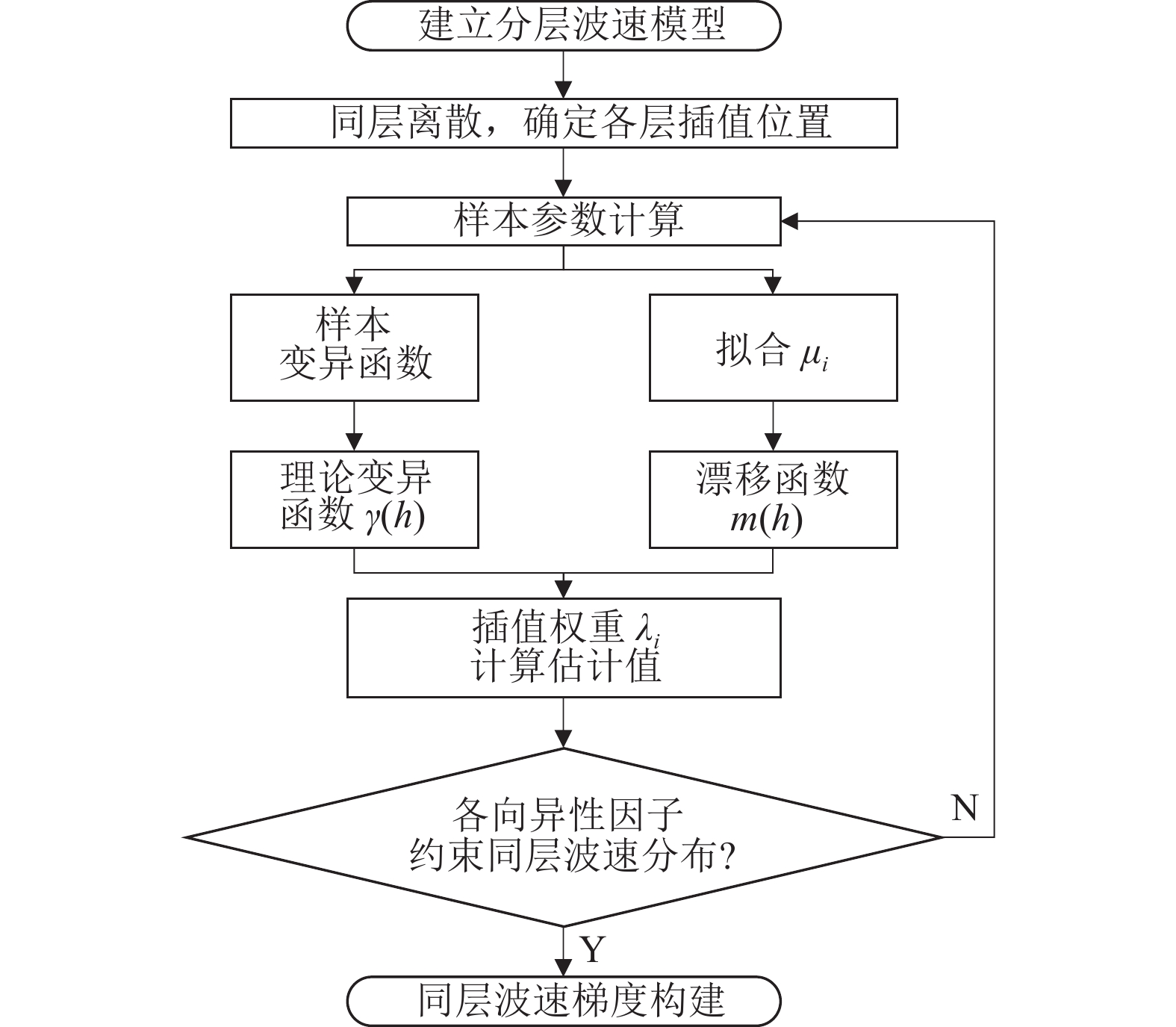
$$ \left\{ \begin{gathered} \sum\limits_{jj = 1}^k {{\lambda _{jj}}\gamma \left( {{h_j} - {h_{jj}}} \right) + {\mu _0} + \sum\limits_{i = 1}^n {{\mu _i}{f^i}\left( {{x_j}} \right)} = \gamma \left( {{x_j} - {x_0}} \right)} \\ \left( {j = 1,2, \cdots ,k} \right) \\ \sum\limits_{j = 1}^k {{\lambda _j} = 1;\sum\limits_{j = 1}^k {{\lambda _j}{f^i}\left( {{x_j}} \right) = {f^i}\left( {{x_0}} \right)} } \;\;\left( {i = 1,2, \cdots ,n} \right) \\ \end{gathered} \right. $$ (8) 初始层状波速模型中构建同层波速梯度的处理过程，如图1所示。首先，通过声波测井资料或地层信息建立初始层状波速模型。其次，根据各岩层岩性参数确定各向异性因子数值，并以初始模型中层间界面位置为每一层插值计算的边界条件。随后以初始波速模型数值为基础，采用泛克里金插值法对每个插值网格节点拟合变异函数及漂移函数，求解对应插值权重，波速分布应服从对应各向异性因子约束。最终，根据插值公式确定各网格节点估计值，赋值后完成波速模型优化。本文仅对P波波速进行讨论。
![]()
图 1 基于泛克里金插值的同层波速梯度构建流程Figure 1. Flow chart showing the construction of wave velocity gradients in the same layer based on universal Kriging interpolation1.2 二次网格搜索
在震源定位过程中，基于层状分布将监测区域划分为网格计算理论走时，从而求解目标函数值的时空分布。由于同层内进行波速梯度插值后，总体网格数量成倍数增加，导致计算效率和成本上升。因此，为在保证计算结果可靠性的基础上提升计算效率，同时适应更复杂的波速模型，参照嵌套网格法，先在粗网格上进行全局搜索，确定震源的大致位置，然后在该区域内使用细网格进行精细搜索，采用二次网格搜索计算理论走时以平衡计算效率与精度之间的关系。
以三层波速模型为例，二次网格搜索策略如图2所示。首先，根据初始层状模型对弹性波传播路径进行求解并计算对应理论走时，再将模型在垂向方向上划分为高程间距为5 m的等高网格单元，然后将每一层网格单元划分为长、宽间距均为d1的均匀三维网格，最后连接各层网格节点，以搜索满足目标函数收敛条件的震源位置及最短传播路径。须注意的是，传播路径应受斯奈尔定理和惠更斯原理约束：弹性波在相邻两层传播时入射角与透射角正弦值之比等于波速之比，且入射路径与透射路径位于分界面的法平面内，如图2a所示。应满足：
![]()
图 2 基于波速插值的传播路径搜索Figure 2. Propagation path search based on wave velocity interpolation$$ \frac{{\sin {\theta _1}}}{{\sin {\theta _2}}} = \frac{{{v_1}}}{{{v_2}}} $$ (9) $$ {{{l}}_{{\mathrm{AB}}}} = \sum\limits_{{{i}} = 1}^2 {\frac{{{{{h}}_{{i}}}}}{{\cos {\theta _{{i}}}}}} $$ (10) $$ {t_{{{AB}}}} = \sum\limits_{i = 1}^2 {\frac{{{h_i}}}{{{v_i}\cos {\theta _i}}}} $$ (11) 式(9)—式(11)联立即可计算弹性波传播理论走时。
初次搜索完成后，采用泛克里金法对各层进行波速梯度插值。随后，合并每一层包含最短传播路径经过节点的4个网格，并将其离散为25个等间距d2的均匀网格。在此基础上，对最优传播路径及对应走时进行二次搜索，并计算震源位置。采用该方法，可在提升震源定位精度的同时降低计算成本。
1.3 目标函数设置及数据处理流程
微震震源定位的本质是全局最优化问题，目标函数的设置对寻优结果影响较大。定位方法采用波形相似叠加法，以亮度函数为目标函数[30]，该方法无需弹性波波相的走时残差(观测到时与理论到时的时差)进行定位，也无需对震相的绝对初至到时进行计算，降低了初至拾取误差的干扰。亮度函数即相似系数S(t)，其表达式为：
$$ S \left( k \right) = \frac{{\displaystyle\sum\nolimits_{j = 1}^N {{{\left( {\displaystyle\sum\nolimits_{i = 1}^M {{f_{ij}}} } \right)}^2}} }}{{N \cdot M \cdot \displaystyle\sum\nolimits_{j = 1}^N {\displaystyle\sum\nolimits_{i = 1}^M {{{\left( {{f_{ij}}} \right)}^2}} } }} $$ (12) 波形相似叠加法通过计算理论走时获取fij数值，无需弹性波波相的走时残差(观测到时与理论到时的时差)进行定位，也无需对震相的绝对初至到时进行计算，降低了初至拾取误差的干扰，更适用于地面微震监测低信噪比微震事件。整个时空中亮点函数取最大时，对应的解即为震源位置和发震时刻。
微震震源定位是水力压裂效果评价的基础和关键，其结果对渗透率反演结果和储层改造体积有重要影响。考虑同层波速梯度情况下，水力压裂微震监测数据处理及效果评价的流程，如图3所示。
![]()
图 3 基于同层波速梯度的水力压裂微震监测及评价流程Figure 3. Flow chart showing the microseismic monitoring and assessment of hydraulic fracturing based on wave velocity gradients in the same layer(1)构建初始层状波速模型，基于泛克里金波速插值和二次网格搜索计算震源坐标。
(2)分析震源空间分布特征，评价破裂范围。
(3)对震源进行时空连接，标定裂缝位置并建立离散裂缝网络。
(4)确定水力裂缝参数，根据参数属性反演渗透率。其中，裂缝尖端位置由震源位置确定，长度、宽度、高度和半径等几何参数由震源半径及震源机制反演结果决定。
(5)计算储层改造体积。剔除空间内距总体微震事件较远的孤立事件点，计算事件点包络体积。
2 压裂与微震监测设计
2.1 工程概况
安徽某矿为煤与瓦斯突出矿井，其
2401 采区位于二水平西翼1煤组，采区内1煤、1上煤为总体倾向NNE的单斜构造，煤层倾角在6°~ 30°，平均13°。1上煤厚2.2~5.2 m，平均3.5 m，1煤厚1.3~4.2 m，平均3.5 m，1上煤与1煤层间距0.6~3.5 m，平均1.1 m，夹层为泥岩。1煤组顶板主要为砂岩，中厚层状，强度高，单轴抗压强度Rc=78.5~132.6 MPa，单轴抗拉强度Rt=5.98~9.65 MPa，稳定性好，总体弱富水性，以静储量为主，易疏干。底板以泥质砂岩为主，Rc=37.5~78.0 MPa，Rt=2.12~7.17 MPa。
由于构造作用导致该矿区煤层渗透率较低，为了提高煤层的气体产能及流体渗透性，煤层顶板水平井分段水力压裂技术逐渐被广泛应用。如图4所示，通过1号L型水平井对煤层进行改造，水平段位于1煤组顶板，自东向西进行分段压裂，井身水平井段共分为9段，总簇数为27簇，各段预计压裂有效影响半径为90 m。
2.2 微震监测台网
基于地面微震监测台站布设范围广，背景噪声复杂的特点，应选取更加便携、高灵敏度、宽频带的监测设备。基于此，本监测工程选取IMU-3C节点式微震监测单元，设备主要参数见表1。
表 1 地面微震监测设备主要技术参数Table 1. Principal technical parameters for the surface microseismic monitoring unit灵敏度/(m·s) 采样率/Hz 频率响应/Hz ADC分辨率/bits 通道/个 76.7 500 0~1 652 24 3 1号水平井水力压裂微震监测台网布置于水平段上方地面(图5)，监测阵列设计为矩形阵列，共布置25个测点。各测点道间距约100 m，监测台网孔径为850 m，约为储层埋深1.3倍，满足现场微震监测要求。台网覆盖面积约1.56 km2，超出压裂预期致裂范围，保证地面监测台网在水平面上对水力压裂范围完全覆盖。前置增益设置为24 dB，以压制噪声干扰。根据奈奎斯特定律，为了避免信号混叠，采样频率至少是信号中最高频率分量的两倍。对于地面微震监测，煤层水力压裂诱发破裂微震信号主频不超过200 Hz，监测设备采样频率则为500 Hz，大于两倍信号主频，满足奈奎斯特定律[31]采样要求，保证了信号的有效采集。
煤层中破裂产生微震信号能量较弱，震源破裂释放的能量随传播距离增加呈指数衰减[32]。为提升检波器安装的稳定性和信号采集质量，将检波器埋设于表土层内，埋深约0.5 m。检波器安装时，调整检波器方位保证指北针向北，并确保水平气泡处于中心，后采用分层压实法(每层厚度10 cm)将表土回填压实，并在安装结束后敲击测试验证信号稳定性。
3 基于泛克里金波速插值的震源定位结果
3.1 波速模型及精度验证
根据1号水平井导眼井声波测井资料结果，建立如图6a所示的层状波速模型。为验证构建同层波速梯度前后震源定位效果差异，分别采用初始层状波速模型、同层波速梯度线性插值及同层波速泛克里金插值后，对3个射孔事件进行定位。本文中设置初次网格搜索的网格间距d1=20 m，二次网格搜索的网格间距d2=8 m。
根据L. Thomsen[26]的研究结果，选取各向异性因子为边界条件对同层波速梯度差异进行约束。采用同层波速线性插值后的波速分布，如图6b所示。根据泛克里金法插值结果可知(图6c)，受垂直方向各向异性影响，初始层状模型中同一层波速分布存在速度梯度，且速度梯度数值非线性分布。这一结果证明，对于地面微震监测，有必要在应用层状波速模型的基础上，进一步考虑同层垂直方向波速的梯度分布以提升微震评价效果的准确性。
选取压裂期间坐标明确的3个射孔事件(表2)为主动震源，验证定位误差，不同波速模型的定位误差见表3。验证结果表明，使用基于泛克里金插值的层状波速模型得到的定位结果误差远低于均一波速模型，定位精度得到明显提升。插值后波速模型对应的垂深方向平均定位误差为3.47 m，处于3~5 m的合理误差范围内，符合微震监测实践的应用标准，同时满足水力压裂效果评价对微震事件精度的要求(通常小于压裂段的有效影响半径的10%)，能够有效反映裂缝展布情况。
表 2 射孔事件参数Table 2. Perforation parameters射孔点 东向坐标/m 北向坐标/m 垂深/m 1 966.67 186.40 −678.47 2 952.72 186.40 −677.52 3 930.78 186.40 −676.22 表 3 不同波速模型定位结果对比Table 3. Comparison of the localization results of varying wave velocity models波速模型 定位误差/m 射孔点1 射孔点2 射孔点3 均一模型 20.67 18.49 17.69 初始层状模型 12.28 11.84 11.37 线性插值模型 10.35 12.49 10.21 泛克里金插值模型 5.24 4.62 6.51 计算程序在同一PC端Python语言环境中运行，泛克里金插值模型的单个震源定位平均计算时间为1.37 s，较初始层状模型和线性插值模型分别仅增加了0.36 s和0.15 s。因此，泛克里金插值法在计算时间差距不大情况下，微震震源定位精度得到进一步提升。
3.2 水力压裂震源定位结果
水力压裂过程中，高压流体注入煤层导致煤体应力失去平衡，煤体结构失稳破坏，所释放的能量以弹性波形式传播至地面微震监测台站。如图7所示，地面台站记录到水力压裂产生的微震事件，但环境中存在一定的背景噪声，采取小波阈值去噪方法[33]进行滤波处理，滤波前原始信号信噪比为4 dB~6 dB，而滤波后信号的信噪比在12 dB~16 dB，表明滤波后信号质量明显提升。统计得到各段压裂产生微震事件数目见表4，九段压裂共产生511个微震事件。
![]()
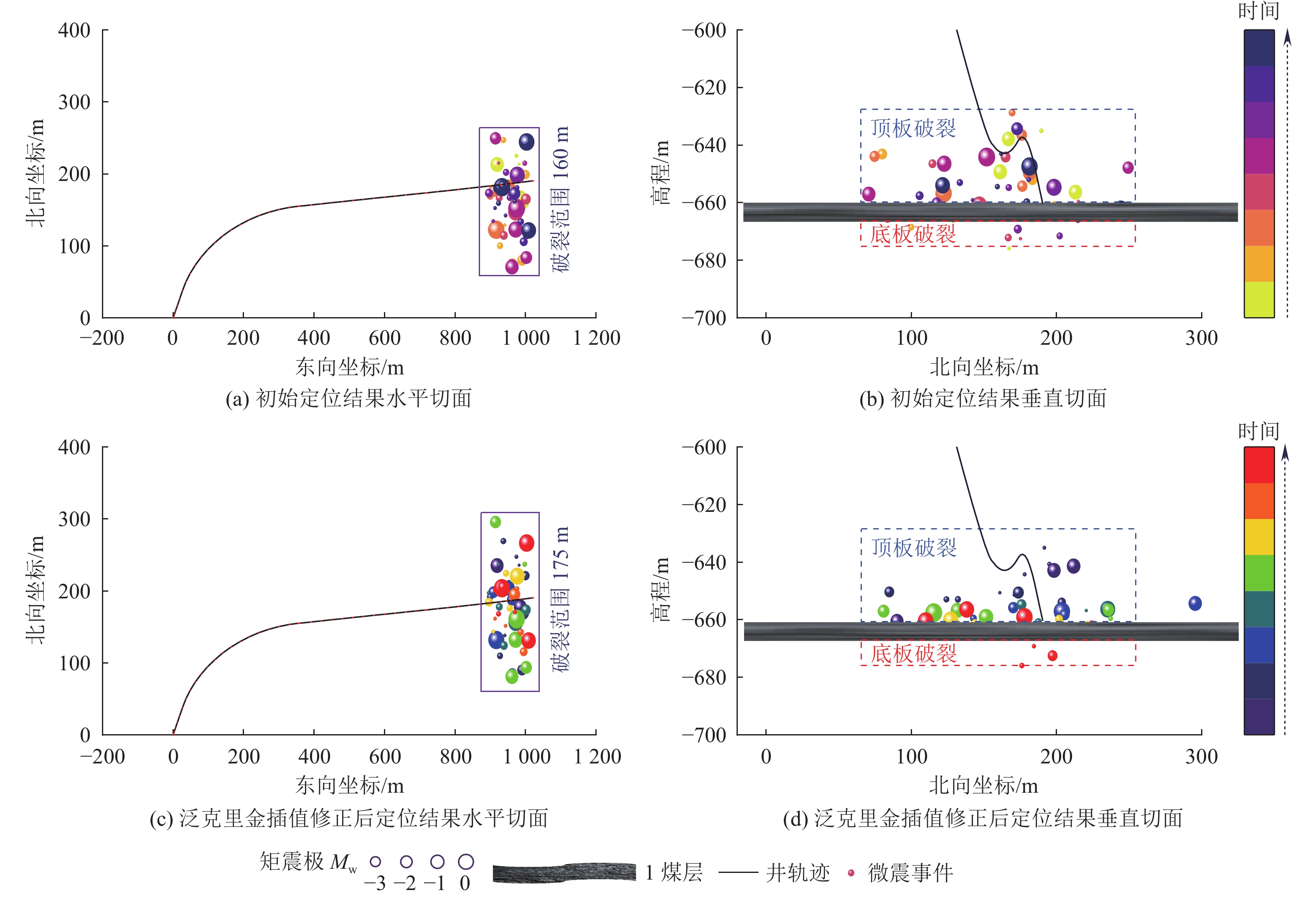
图 7 水力压裂微震事件原始信号Figure 7. Original signals of hydraulic fracturing-induced microseismic events表 4 1号井各压裂段微震事件数量Table 4. Quantities of microseismic events in various fracturing segments of horizontal well No.1压裂段 1 2 3 4 5 6 7 8 9 微震事件个数 50 76 57 47 53 76 45 46 61 经过震源定位计算，得到煤层水力压裂微震事件定位结果。以首段压裂为例(图8)，高压流体注入后，首先在井筒附近产生小能量破裂。随后，破裂区域向垂直于井筒方向延伸，伴随着较大能量微震事件的产生。最终，由于高压流体持续注入，井筒四周煤岩体结构失稳加剧，破裂形成多个大能量微震事件。
![]()
图 8 1号井第一压裂段水力压裂微震事件定位结果Figure 8. Localization results of hydraulic fracturing-induced microseismic events in the first fracturing segment of horizontal well No.1如图8所示，在有无同层波速插值2种情况下，震源定位结果存在显著差异。对于垂向定位结果，压裂点高程约–656 m，原始定位结果在垂向的分布范围为–676 ~–628 m，微震事件主要存在于煤层上方顶板。煤层内微震事件数量较少，仅产生9个破裂，与煤层下方底板微震事件数量相同，压裂后期诱发破裂主要出现在顶板(图8b)。这一结果不符合顶板破裂沟通煤层诱发规模破裂的特点，表明定位结果垂向分布存在一定误差[34-35]。在通过波速插值对弹性波传播路径进行修正后，定位结果的垂向分布范围为–675~–634 m。煤层下方层位内微震事件数量减少，且煤层内诱发破裂数量增加至22个(图8d)。高压流体注入首先诱发顶板上部破裂，破裂随后发展至顶板与煤层交界面，并在压裂中后期造成煤层内部产生规模破裂。不同层位内微震事件时空分布，证明经过同层波速插值的波速模型对水力压裂效果评价更为合理。
对于水平投影方向，引入同层波速插值后，南北走向微震事件分布范围增加了约15 m(图8a和图8c)。且震源空间位置呈现向北平移的趋势，压裂井两侧微震事件对称性增强。在射孔垂直向下且压裂层位缺乏明显开采扰动和地质构造活动的环境下，认为水平方向微震震源近似对称分布的结果更合理[36]。
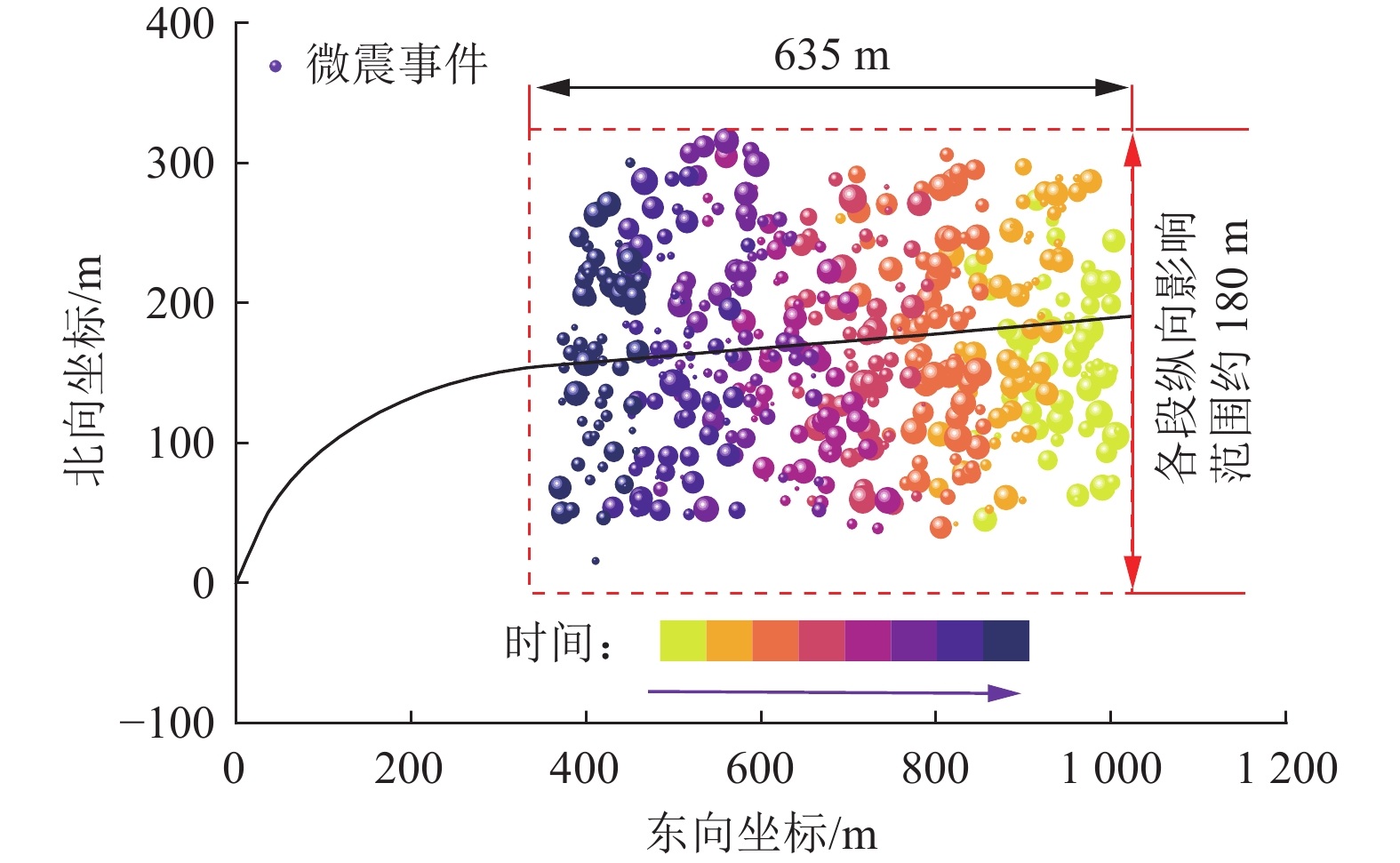
基于同层波速插值及二次网格搜索，利用震源扫描法得到9段压裂微震事件的时空位置，水平方向分布如图9所示。沿压裂井轨迹方向，水力压裂诱发微震事件横向分布约635 m，首尾超出射孔段共约65 m。根据微震事件发震时刻及空间坐标，发现前后两压裂段之间存在微震事件的交叉，说明各压裂段诱发破裂区域存在重叠效应。以水平井段为对称轴，各压裂段微震事件纵向分布范围为170~180 m，有效影响半径约90 m。破裂范围符合压裂设计预期效果。
![]()
图 9 水力压裂9段微震事件水平切面分布Figure 9. Horizontal sectional distribution of hydraulic fracturing-induced microseismic events in nine fracturing segments4 水力压裂微震评价
4.1 压裂过程及微震响应
水力压裂过程中，液体的注入导致煤体失稳破坏，选取总液量最大与最小的两段(图10)，对压裂过程及其微震响应进行评价分析。
如图10a所示，第2压裂段，随着试压结束，排量在投球及调试阶段呈阶梯式增长，套管压力以相同趋势上升，导致射孔段周围低强度煤岩体失稳，产生数个微震事件。以阶梯式增长方式注入前置液后，套管压力总体随排量增大而上升。该阶段产生较多微震事件，中后期微震事件密集度增加。前置液注入完成后，通过注入携砂液实现多尺度复杂裂缝体系内裂缝支撑效果，该过程中排量稳定保持在最高水平，压力较前置液注入阶段有所上升。这一过程中，压裂裂缝进一步发育贯通，能量的释放导致微震事件不断产生，最大破裂能量矩震级Mw达到–0.52。停泵之后，仍监测到数个微震事件，且出现该段压裂最大能量破裂，Mw为–0.41。表明停泵之后，应力场未达到平衡，持续诱发裂缝产生，直至煤岩体结构恢复稳定[37]。
如图10b所示，第7段压裂过程微震响应与第2段存在差异。第7段微震事件发震时间主要分布于前置液注入阶段，最大能量破裂矩震级为–0.88，也在前置液注入期间产生。其原因可能是由于第7段压裂位置对应煤岩体裂隙贯通性能良好，前置液注入阶段裂缝已充分发育，导致携砂液注入阶段产生的破裂较少。
总的来看，水力压裂过程中，微震事件时序分布及能量演化特征与压裂参数变化趋势一致，水力压裂的微震响应与压裂工艺具有良好的相关性。
4.2 压裂区域渗透率变化
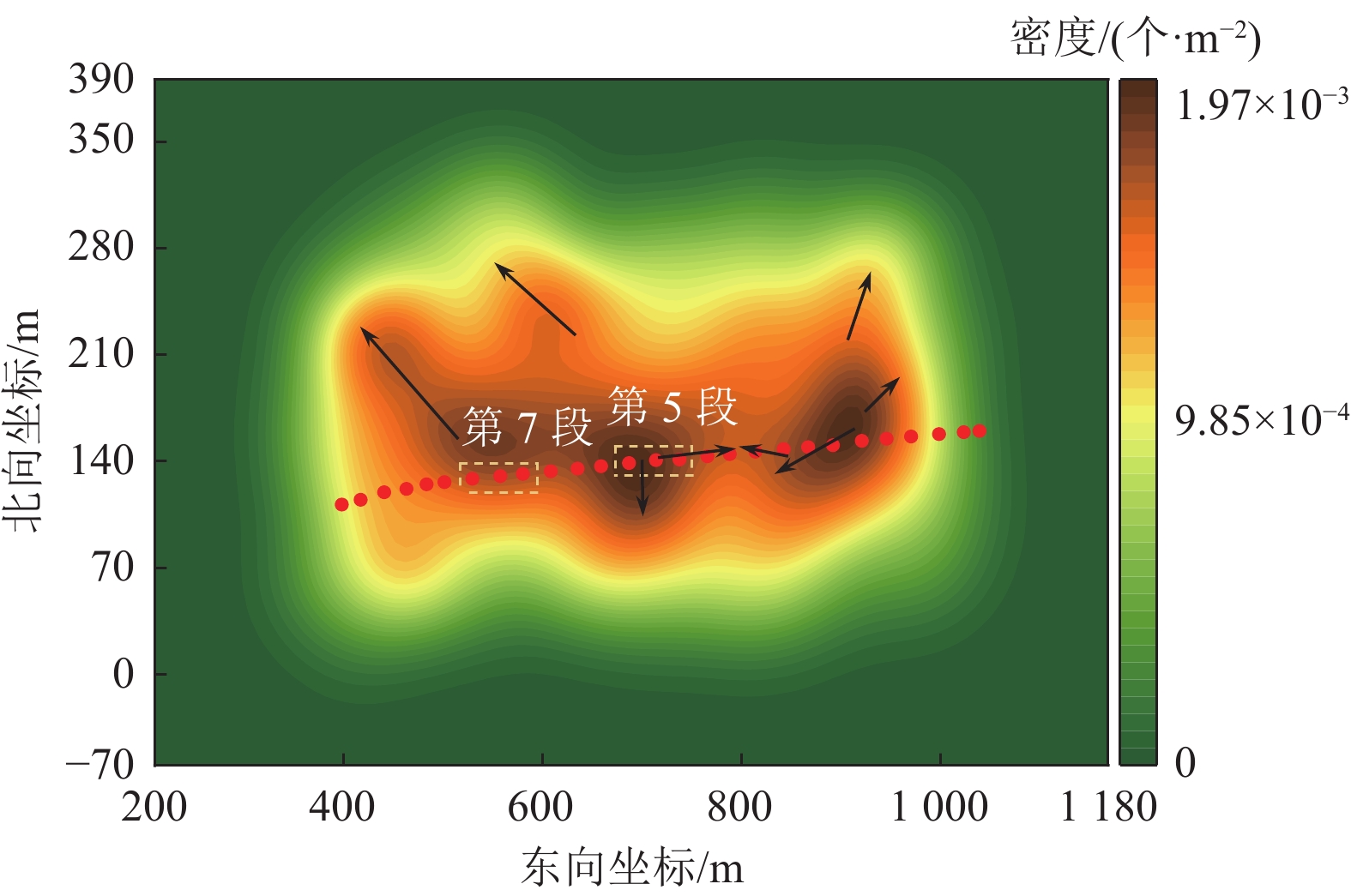
基于泛克里金波速插值的微震源定位方法，确定了破裂点的时空关系，为压裂改造效果评价提供了基础。根据储层深度单位面积内诱发破裂发生频次，得到水平方向微震事件分布密度(图11)，微震事件密度越高，表明该区域诱发破裂活动越频繁。
![]()
图 11 水力压裂诱发微震事件密度水平方向分布Figure 11. Horizontal density distribution of hydraulic fracturing-induced microseismic events第5段与第7段对应射孔范围内微震事件分布最密集，说明这2个压裂段诱发破裂发生最频繁，对高压流体注入形成的扰动更敏感。最大密度达每平方米1.97×10–3个微震事件，即约500 m2区域内产生一次诱发破裂。各段微震事件密度总体相对压裂井对称分布，水力压裂改造区域由井筒向四周延伸，其走向无明显规律。
微震事件分布密度仅表征了各压裂段诱发破裂的密集程度，但未考虑破裂能量对储层改造的影响，难以量化改造效果。根据Oda模型[38]求解渗透率量化评价方法，将三维网格内诱发破裂事件等效为离散裂缝，将压裂区域切割为边长为10 m的正方体单元。随后根据每个体积单元内微震事件的震级大小、离散裂缝的数量和裂缝几何参数进行统计计算，得到各压裂段的渗透率分布[39]。1煤储层深度水平剖面渗透率如图12所示。
![]()
图 12 储层裂缝水平剖面渗透率Figure 12. Permeability of the horizontal section of reservoir fractures对于各压裂段，渗透率随裂缝扩展整体呈纵向。各段井筒附近均出现渗透率数值较高区域，部分压裂段外围也分布有高渗透率区域。储层深度微震事件密度分布与渗透率分布存在差异，微震事件高密度区域存在裂缝未贯通的情况，后期可采取重复压裂措施提高裂缝发育程度。
总的来看，第2段及第9段近井筒区域压裂效果最好，井筒附近形成了高渗透率联通区，排采时可增加在该区域的瓦斯抽采时间。
4.3 压裂效果对比分析
储层渗透率和储层改造体积(stimulated reservoir volume，SRV)是影响压裂井抽采效率的主要因素。依据同层波速梯度模型校正后的震源位置，拟合三维破裂空间，可实现改造空间及SRV的量化表征(图13)。
![]()
图 13 1号水平井压裂诱发微震事件Figure 13. Hydraulic fracturing-induced microseismic events in horizontal well No.1采用最小体积覆盖椭球法对SRV进行计算，其原理为采用几何包络法，该方法先将空间中离散的微震事件点剔除，再基于微震事件空间分布生成凸包体，该凸包体体积即为SRV大小。
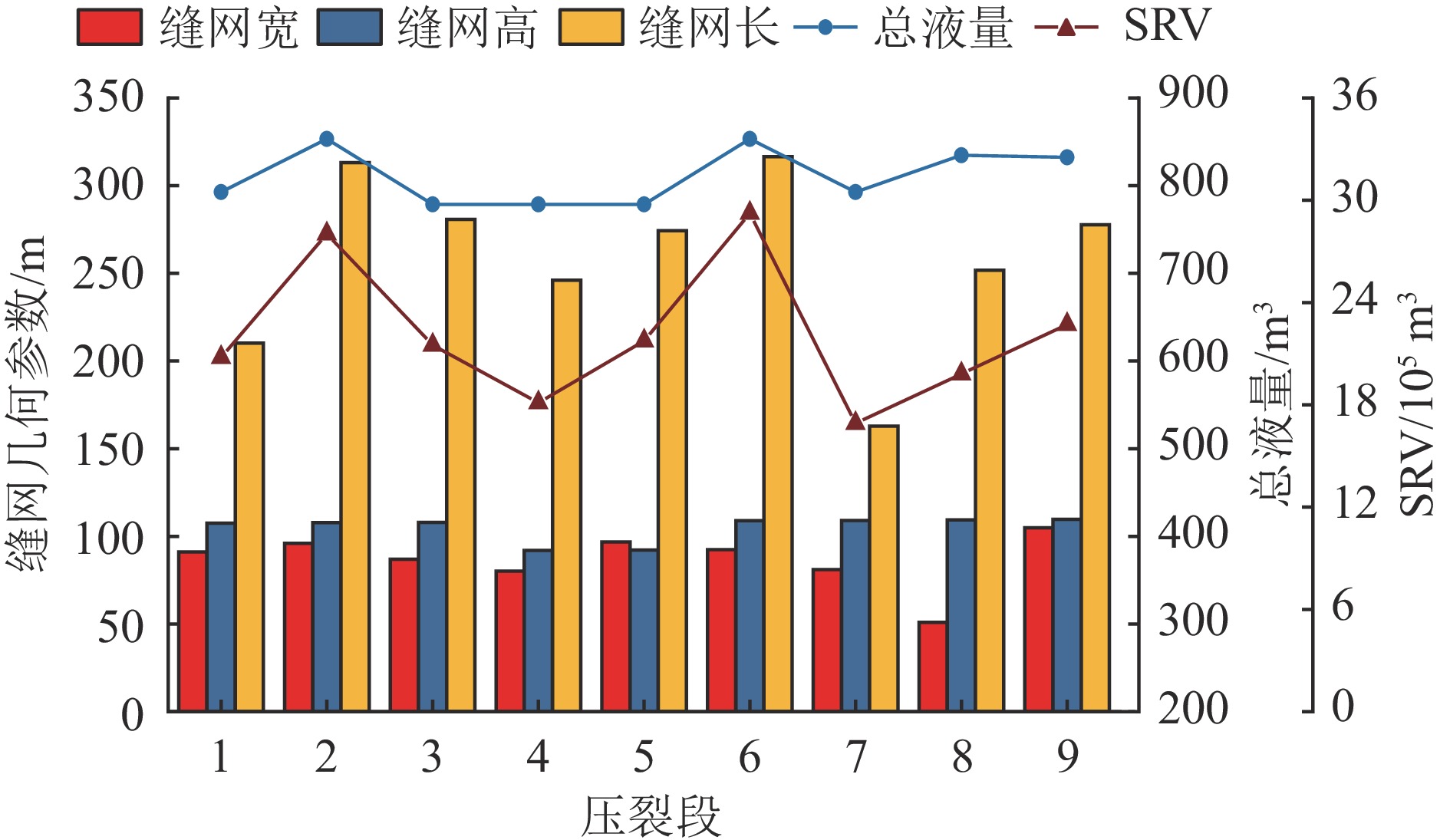
图13a为水力压裂诱发微震事件时空分布，水平井分段压裂形成了立体破裂区域，使储层原有结构得到改造。根据微震事件的空间特征计算1号水平井各段SRV，其空间结构如图13b所示，SRV沿微震事件空间分布形成包络腔体，该腔体内未发现明显的空白区域，与微震事件空间位置对应关系良好。统计得到各压裂段SRV大小(表5)，以及水力裂缝相关参数与压裂流量的关系(图14)。
表 5 1号水平井各压裂段SRVTable 5. SRVs in various fracturing segments of horizontal well No.1压裂段 1 2 3 4 5 6 7 8 9 总计 SRV/105 m3 20.6 28.0 21.3 18.1 21.7 29.1 16.7 19.7 22.5 197.7 ![]()
图 14 水平井各压裂段总液量与裂缝参数关系Figure 14. Relationships between total volume of injected fluids and frac-ture parameters in various fracturing segments of horizontal well No.1水力裂缝长度和SRV与各段压裂注入总液量整体呈正相关关系，第2段与第6段注入总液量分别达到852.38 m3和853.34 m3，对应的缝网长度分别为312 m和316 m。第7段缝网长度最小为160 m，该段总液量为791.02 m3。各压裂段缝网高无明显差别，第4段和第5段缝网高为90 m，其余各段缝网高均为108 m。除第4段外，SRV与总液量变化趋势一致，该段SRV的异常变化说明，煤层水力压裂效果受压裂工艺和地质条件等多种因素控制。第2段与第6段SRV最高，分别达到28.0×105 m3和29.1×105 m3。安徽某矿1号水平井分段压裂SRV总计为1.977×107 m3，压裂效果符合预期目标，证明了地面水平井煤层压裂以及地面微震监测在煤矿瓦斯灾害防治中的有效性。
5 结 论
(1) 相较于初始层状波速模型，采用泛克里金同层波速插值的波速模型能够有效提高煤层水平井分段水力压裂效果的震源定位精度。对于同一射孔点，泛克里金插值后波速模型定位误差最高降低了7.22 m，最低绝对误差达到4.62 m，较初始层状模型平均降低了70.92%，较线性插值模型平均降低了49.54%。
(2) 采用泛克里金同层波速插值对弹性波传播路径修正后，微震事件在垂向方向离散性得到有效约束，微震事件在南北走向的分布增强了水力压裂井的对称性，其时空分布符合诱发破裂规律。各压裂段有效影响半径约90 m。微震事件时序分布及能量演化特征与压裂参数变化趋势一致，水力压裂的微震响应与压裂工艺具有良好的相关性。
(3) 1号水平井各压裂段共诱发511个微震事件，其时序及能量演化特征与压裂工艺一致。水力裂缝长度和SRV与各压裂段注入总液量正相关，第2段与第6段总液量最高，缝网长度分别为312 m和316 m，SRV分别达到28.0×105 m3和29.1×105 m3。1号水平井压裂SRV总计为1.977×107 m3，压裂改造效果与预期结果相符。
符号注释：
cij为岩体弹性模量独立分量，Pa，其中，i，j为应力与应变分量在各主轴方向上的索引；d1为网格单元长宽间距，m；E为数学期望；$f^i(h) $为漂移项中用于空间位置表达的趋势基函数值，m；$f^i(x_j) $为第i个趋势基函数在位置xj的值，m；$f^i(x_0) $为第i个趋势基函数在插值点x0的值，m；fij为时窗内第i道的第j个采样点数据幅值，m；h为煤岩层深度，m；h0为目标煤岩层的深度，m；hi为第i个已知煤岩层样本点的深度，m；hj为第j个已知煤岩层样本点的深度，m；hjj为第j个已知煤岩层样本点与第jj个已知煤岩层样本点之间的深度差，m；k为时窗中心位置；lAB为点A至点B的传播路径，m；m(h)为深度为h的确定性漂移函数，m/s；m(h0)为深度为h0的确定性漂移函数；m(hi)为深度为hi的确定性漂移函数；M为参与计算的地震道数目；Mw为矩震级；n为用于泛克里金插值的已知采样点数量；N为滑动时窗内采样点数量；r(h)为期望为0的残差；R为井眼轨迹的曲率半径，m；S(k)为相似系数；tAB为点A到点B的走时，s；v1、v2分别为弹性波在第一层和第二层介质中的波速，m/s；Var[·]为方差运算符，m2/s2；Z(h)为深度h处波速值，m/s；xj、x0为插值点和样本点的空间位置坐标，m；Z(h+Δh)为与深度h间距Δh深度的另一点处的波速值，m/s；Z(h0)为目标点深度h0处的波速值，m/s；$\hat Z\left( {{h_0}} \right)$为目标点深度h0处的泛克里金波速预测值，m/s；Z(hi+Δh)为与深度hi间距Δh深度的另一点处的波速值，m/s；μ0为目标采样点的浮动系数；μi为第i个采样点的浮动系数；λi、λj分别为第i个、j个采样点的克里金权重；λjj为第j个采样点对应的克里金权重项与变异函数项的组合，用于表达采样点间的空间相关性；θ1、θ2分别为弹性波在层间界面的入射角和透射角，(°)；δ为对称轴P波波速，m/s；ε为P波各向异性参数；γ为S波各向异性强度参数；γ(Δh)为变异函数，m2/s2；γ(hj−hi)为采样点对之间的变异函数值，m2/s2；$\hat \gamma \left( {\Delta h} \right)$为经验变异函数，m2/s2；Δh为位置深度增量，m；nΔh是分离间距为Δh的采样点对个数。
-
![]()
图 1 基于泛克里金插值的同层波速梯度构建流程
Fig. 1 Flow chart showing the construction of wave velocity gradients in the same layer based on universal Kriging interpolation
![]()
图 3 基于同层波速梯度的水力压裂微震监测及评价流程
Fig. 3 Flow chart showing the microseismic monitoring and assessment of hydraulic fracturing based on wave velocity gradients in the same layer
![]()
图 7 水力压裂微震事件原始信号
Fig. 7 Original signals of hydraulic fracturing-induced microseismic events
![]()
图 8 1号井第一压裂段水力压裂微震事件定位结果
Fig. 8 Localization results of hydraulic fracturing-induced microseismic events in the first fracturing segment of horizontal well No.1
![]()
图 9 水力压裂9段微震事件水平切面分布
Fig. 9 Horizontal sectional distribution of hydraulic fracturing-induced microseismic events in nine fracturing segments
![]()
图 11 水力压裂诱发微震事件密度水平方向分布
Fig. 11 Horizontal density distribution of hydraulic fracturing-induced microseismic events
![]()
图 12 储层裂缝水平剖面渗透率
Fig. 12 Permeability of the horizontal section of reservoir fractures
![]()
图 13 1号水平井压裂诱发微震事件
Fig. 13 Hydraulic fracturing-induced microseismic events in horizontal well No.1
![]()
图 14 水平井各压裂段总液量与裂缝参数关系
Fig. 14 Relationships between total volume of injected fluids and frac-ture parameters in various fracturing segments of horizontal well No.1
表 1 地面微震监测设备主要技术参数
Table 1 Principal technical parameters for the surface microseismic monitoring unit
灵敏度/(m·s) 采样率/Hz 频率响应/Hz ADC分辨率/bits 通道/个 76.7 500 0~1 652 24 3 
下载: 导出CSV
表 2 射孔事件参数
Table 2 Perforation parameters
射孔点 东向坐标/m 北向坐标/m 垂深/m 1 966.67 186.40 −678.47 2 952.72 186.40 −677.52 3 930.78 186.40 −676.22
下载: 导出CSV
表 3 不同波速模型定位结果对比
Table 3 Comparison of the localization results of varying wave velocity models
波速模型 定位误差/m 射孔点1 射孔点2 射孔点3 均一模型 20.67 18.49 17.69 初始层状模型 12.28 11.84 11.37 线性插值模型 10.35 12.49 10.21 泛克里金插值模型 5.24 4.62 6.51
下载: 导出CSV
表 4 1号井各压裂段微震事件数量
Table 4 Quantities of microseismic events in various fracturing segments of horizontal well No.1
压裂段 1 2 3 4 5 6 7 8 9 微震事件个数 50 76 57 47 53 76 45 46 61
下载: 导出CSV
表 5 1号水平井各压裂段SRV
Table 5 SRVs in various fracturing segments of horizontal well No.1
压裂段 1 2 3 4 5 6 7 8 9 总计 SRV/105 m3 20.6 28.0 21.3 18.1 21.7 29.1 16.7 19.7 22.5 197.7
下载: 导出CSV
-
[1] 杨长鑫,杨兆中,李小刚,等. 中国煤层气地面井开采储层改造技术现状与展望[J]. 天然气工业,2022,42(6):154−162. YANG Changxin,YANG Zhaozhong,LI Xiaogang,et al. Status and prospect of reservoir stimulation technologies for CBM surface well production in China[J]. Natural Gas Industry,2022,42(6):154−162.
[2] LI Lei,TAN Jingqiang,SCHWARZ B,et al. Recent advances and challenges of waveform–based seismic location methods at multiple scales[J]. Reviews of Geophysics,2020,58(1):e2019RG000667.
[3] 闫江平,庞长庆,段建华,等. 煤矿井下水力压裂范围微震监测技术及其影响因素[J]. 煤田地质与勘探,2019,47(增刊1):92−97. YAN Jiangping,PANG Changqing,DUAN Jianhua,et al. Microseismic monitoring of underground hydraulic fracturing range in coal seam and analysis of influencing factors[J]. Coal Geology & Exploration,2019,47(Sup.1):92−97.
[4] LI Lei,TAN Jingqiang,WOOD D A,et al. A review of the current status of induced seismicity monitoring for hydraulic fracturing in unconventional tight oil and gas reservoirs[J]. Fuel,2019,242:195−210.
[5] 王国举,赵立松,高刚,等. 基于井下煤层水力压裂的微震时空发育规律研究[J]. 煤炭技术,2024,43(5):207−211. WANG Guoju,ZHAO Lisong,GAO Gang,et al. Study on time–space development law of microseism based on hydraulic fracturing of underground coal seam[J]. Coal Technology,2024,43(5):207−211.
[6] ZHOU Jian,SHEN Xiaojie,QIU Yingui,et al. Cross–correlation stacking–based microseismic source location using three metaheuristic optimization algorithms[J]. Tunnelling and Underground Space Technology,2022,126:104570.
[7] 曹安业,王常彬,杨旭,等. 微震定位精度影响下采场裂隙表征与冲击地压预警[J]. 煤炭科学技术,2024,52(2):1−9. CAO Anye,WANG Changbin,YANG Xu,et al. Fractures characterization in mining field considering seismic location accuracy and its application on pre–warning coal burst hazards[J]. Coal Science and Technology,2024,52(2):1−9.
[8] LI Lei,TAN Jingqiang,ZHANG Dazhou,et al. FDwave3D:A MATLAB solver for the 3D anisotropic wave equation using the finite–difference method[J]. Computational Geosciences,2021,25(5):1565−1578.
[9] 黄晓红,孙国庆,张凯月. 基于全相位多次互相关的Geiger声发射源定位方法[J]. 岩土力学,2018,39(4):1362−1368. HUANG Xiaohong,SUN Guoqing,ZHANG Kaiyue. Localisation of Geiger acoustic emission source based on all–phase analysis and several times cross–correlation[J]. Rock and Soil Mechanics,2018,39(4):1362−1368.
[10] 李健,高永涛,谢玉玲,等. 基于无需测速的单纯形法微地震定位改进研究[J]. 岩石力学与工程学报,2014,33(7):1336−1346. LI Jian,GAO Yongtao,XIE Yuling,et al. Improvement of microseism locating based on simplex method without velocity measuring[J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(7):1336−1346.
[11] HOBRO J,WILLIAMS M,CALVEZ J L. The finite–difference method in microseismic modeling:Fundamentals,implementation,and applications[J]. The Leading Edge,2016,35(4):362−366.
[12] 余金柱,王嘉鑫,李建辉,等. 基于微震事件时空分布特征的连续裂缝网络建模方法研究:以致密砂岩储层重复压裂效果评价为例[J]. 地球物理学进展,2024,39(6):2275−2285. YU Jinzhu,WANG Jiaxin,LI Jianhui,et al. Continuous fracture network modeling based on microseismic event spatial–temporal characteristics:A case study of refrac evaluation of tight oil reservoir[J]. Progress in Geophysics,2024,39(6):2275−2285.
[13] 陈炳瑞,冯夏庭,李庶林,等. 基于粒子群算法的岩体微震源分层定位方法[J]. 岩石力学与工程学报,2009,28(4):740−749. CHEN Bingrui,FENG Xiating,LI Shulin,et al. Microseism source location with hierarchical strategy based on particle swarm optimization[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(4):740−749.
[14] 巩思园,窦林名,马小平,等. 煤矿矿震定位中异向波速模型的构建与求解[J]. 地球物理学报,2012,55(5):1757−1763. GONG Siyuan,DOU Linming,MA Xiaoping,et al. Study on the construction and solution technique of anisotropic velocity model in the location of coal mine tremor[J]. Chinese Journal of Geophysics,2012,55(5):1757−1763.
[15] WANG Yi,SHANG Xueyi,PENG Kang. Relocating mining microseismic earthquakes in a 3–D velocity model using a windowed cross–correlation technique[J]. IEEE Access,2020,8:37866−37878.
[16] FENG Qiang,HAN Liguo,PAN Baozhi,et al. Microseismic source location using deep reinforcement learning[J]. IEEE Transactions on Geoscience and Remote Sensing,2022,60:4510209.
[17] HUANG Guojiao,BA Jing,DU Qizhen,et al. Simultaneous inversion for velocity model and microseismic sources in layered anisotropic media[J]. Journal of Petroleum Science and Engineering,2019,173:1453−1463. DOI: 10.1016/j.petrol.2018.10.071
[18] 张晓平,朱航凯,刘泉声,等. 基于斯奈尔定律及布谷鸟算法的层状岩体微震定位研究[J]. 岩石力学与工程学报,2021,40(7):1383−1391. ZHANG Xiaoping,ZHU Hangkai,LIU Quansheng,et al. Research on microseismic event locating in layered rock masses based on Snell’s law and Cuckoo search algorithm[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(7):1383−1391.
[19] 徐港,薛传荣,王鑫科,等. 考虑地震波折射的层状介质微震源定位方法[J]. 岩石力学与工程学报,2021,40(8):1654−1663. XU Gang,XUE Chuanrong,WANG Xinke,et al. A microseismic source location method considering refraction of seismic waves in layered media[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(8):1654−1663.
[20] STIERLE E,VAVRYČUK V,KWIATEK G,et al. Seismic moment tensors of acoustic emissions recorded during laboratory rock deformation experiments:Sensitivity to attenuation and anisotropy[J]. Geophysical Journal International,2016,205(1):38−50.
[21] GRECHKA V,YASKEVICH S. Azimuthal anisotropy in microseismic monitoring:A Bakken case study[J]. Geophysics,2014,79(1):KS1−KS12.
[22] ZHENG Yikang,WANG Yibo. Sensitivity analysis of anisotropic parameter inversion simultaneously with microseismic source location in layered VTI media[J]. Frontiers in Earth Science,2022,10:1023141.
[23] WANG Xiaoming,XIAO Yuanjie,LI Wenqi,et al. Kriging–based surrogate data–enriching artificial neural network prediction of strength and permeability of permeable cement–stabilized base[J]. Nature Communications,2024,15(1):4891.
[24] CHAGAS V B P,CHAFFE P L B,BLÖSCHL G. Climate and land management accelerate the Brazilian water cycle[J]. Nature Communications,2022,13(1):5136. DOI: 10.1038/s41467-022-32580-x
[25] 吴顺川,郭超,高永涛,等. 岩体破裂震源定位问题探讨与展望[J]. 岩石力学与工程学报,2021,40(5):874−891. WU Shunchuan,GUO Chao,GAO Yongtao,et al. Discussion and prospect of source location of rock fracture[J]. Chinese Journal of Rock Mechanics and Engineering,2021,40(5):874−891.
[26] THOMSEN L. Weak elastic anisotropy[J]. Geophysics,1986,51(10):1954−1966.
[27] MUKHOPADHYAY T,CHAKRABORTY S,DEY S,et al. A critical assessment of Kriging model variants for high–fidelity uncertainty quantification in dynamics of composite shells[J]. Archives of Computational Methods in Engineering,2017,24(3):495−518.
[28] SINHA A,SHAIKH V. Solving bilevel optimization problems using Kriging approximations[J]. IEEE Transactions on Cybernetics,2022,52(10):10639−10654.
[29] 王长虹,朱合华,钱七虎. 克里金算法与多重分形理论在岩土参数随机场分析中的应用[J]. 岩土力学,2014,35(增刊2):386−392. WANG Changhong,ZHU Hehua,QIAN Qihu. Application of Kriging methods and multi–fractal theory to estimate of geotechnical parameters spatial distribution[J]. Rock and Soil Mechanics,2014,35(Sup.2):386−392.
[30] KAO H,SHAN Shaoju. The source–scanning algorithm:Mapping the distribution of seismic sources in time and space[J]. Geophysical Journal International,2004,157(2):589−594. DOI: 10.1111/j.1365-246X.2004.02276.x
[31] ZHANG Ran,HU Qingsong,WANG Gang,et al. Distributed compressed sensing of microseismic signals through first break time extraction and signal alignment[J]. IEEE Access,2018,6:27408−27417. DOI: 10.1109/ACCESS.2018.2830974
[32] 姜玉龙,王开,蔡婷婷,等. 不同注液速率水力压裂多裂缝扩展规律研究[J]. 煤炭工程,2024,56(8):183−189. JIANG Yulong,WANG Kai,CAI Tingting,et al. Multi–fracture expansion law of hydraulic fracturing with different injection rates[J]. Coal Engineering,2024,56(8):183−189.
[33] LI Huailiang,SHI Jiahao,LI Linjia,et al. Novel wavelet threshold denoising method to highlight the first break of noisy microseismic recordings[J]. IEEE Transactions on Geoscience and Remote Sensing,2022,60:5910110.
[34] ZHANG Fangxue,WANG Ruijia,CHEN Yunfeng,et al. Spatiotemporal variations in earthquake triggering mechanisms during multistage hydraulic fracturing in Western Canada[J]. Journal of Geophysical Research:Solid Earth,2022,127(8):e2022JB024744. DOI: 10.1029/2022JB024744
[35] ZHANG Fengshou,DAMJANAC B,MAXWELL S. Investigating hydraulic fracturing complexity in naturally fractured rock masses using fully coupled multiscale numerical modeling[J]. Rock Mechanics and Rock Engineering,2019,52(12):5137−5160.
[36] THIEL S. Electromagnetic monitoring of hydraulic fracturing:Relationship to permeability,seismicity,and stress[J]. Surveys in Geophysics,2017,38(5):1133−1169. DOI: 10.1007/s10712-017-9426-2
[37] YU Shuyang,REN Xuhua,ZHANG Jixun,et al. An improved smoothed particle hydrodynamics method and its application in rock hydraulic fracture modelling[J]. Rock Mechanics and Rock Engineering,2021,54(12):6039−6055. DOI: 10.1007/s00603-021-02594-w
[38] ODA M. Permeability tensor for discontinuous rock masses[J]. Géotechnique,1985,35(4):483−495.
[39] ZHAO Yong,YANG Tianhong,ZHANG Penghai,et al. Method for generating a discrete fracture network from microseismic data and its application in analyzing the permeability of rock masses:A case study[J]. Rock Mechanics and Rock Engineering,2019,52(9):3133−3155. DOI: 10.1007/s00603-018-1712-x
计量
- 文章访问数: 55
- HTML全文浏览量: 8
- PDF下载量: 18
