Intelligent identification of the acoustic emission characteristics and crack propagation states during of coal failure based on the NRBO-XGBoost model
-
摘要:目的
煤岩动力灾害事故与煤岩破坏的复杂性和不确定性密切相关，准确识别煤体裂纹扩展状态是研究其失稳破坏的重要途径，目前基于声发射物理量信息的识别方法存在速度慢、效率低等问题，难以满足煤矿安全、高效和智能化开采需求。
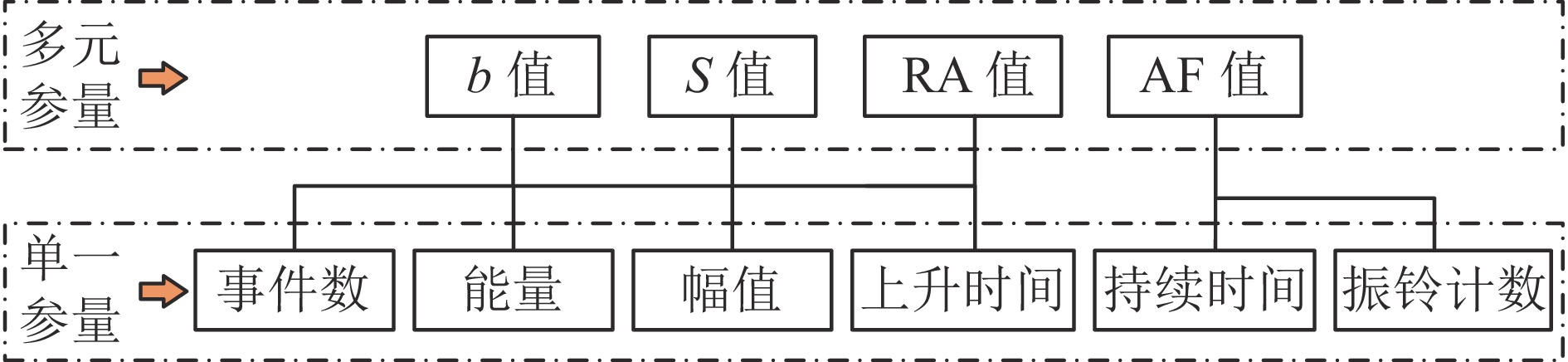
方法为实现煤体裂纹扩展状态的智能识别，通过分布式梯度增强库(XGBoost)构建一种基于牛顿−拉夫逊优化算法(NRBO)的优化模型，建立声发射震级−频度关系b值、活跃度S值及破裂类型RA-AF值等多元参量与煤体裂纹扩展状态的对应关系，通过开展煤体破坏声发射监测试验，得到声发射多元信号数据，并以此作为训练样本，利用NRBO-XGBoost模型对不同加载速率下煤体的裂纹稳定扩展(Ⅲ)和不稳定扩展(Ⅳ)阶段进行智能识别，实现XGBoost参数的自适应寻优，采用准确率、精确率、召回率及F1值4项指标评估各模型的性能。
结果和结论结果表明：(1) 在Ⅲ阶段，煤体b值和S值均小幅度升高，剪切裂纹所占比例减少，进入Ⅳ阶段后，b值和剪切裂纹占比呈相反变化趋势，S值大幅度升高；随着加载速率增加，b值波动水平和幅度均降低、S值升高幅度减小、剪切裂纹所占的比例增加幅度增大。(2) 建立的NRBO-XGBoost模型实现了由声发射多元参量到煤体裂纹扩展状态的智能识别。(3) 同XGBoost和PSO-XGBoost模型的4项评估指标对比，NRBO-XGBoost模型下低和高加载速率样本分别达到90.69%、88.79%、99.00%、93.62%和82.76%、86.76%、88.50%、87.62%，效果最优。研究成果为声发射技术在煤体裂纹扩展状态识别与智能监测研究提供了新的思路，利用实测声发射数据建立预测模型，可实现煤岩动力灾害的监测、预警。
Abstract:ObjectiveThe dynamic hazards of coals are intimately associated with the complexity and uncertainty of coal failure, while accurately identifying the propagation states of coal cracks serves as a critical approach to investigating the instability failure of coals. However, the current identification methods based on the physical quantities of acoustic emission suffer from slow speeds and low efficiency, failing to meet the demand for safe, efficient, and intelligent mining of coal mines.
MethodsTo achieve the intelligent identification of the crack propagation states of coals, this study constructed an optimization model based on the Newton-Raphson-based optimizer (NRBO) and the eXtreme Gradient Boosting (XGBoost)—a distributed gradient boosting library (also referred to as the NRBO-XGBoost model). Then, this study determined the corresponding relationships of multivariate parameters (i.e., values b representing the relationship between acoustic emission magnitude and frequency, S representing the activity, and RA and AF representing the fracture types) with the crack propagation states of coals. Using experiments on acoustic emission monitoring of coal failure, this study acquired the multivariate signal data of acoustic emission, which were subsequently used as training samples. Employing the NRBO-XGBoost model, this study performed intelligent identification of the stable and unstable crack propagation stages (stages Ⅲ and Ⅳ, respectively) of coals under varying loading rates, achieving adaptive optimization of XGBoost parameters. Furthermore, this study evaluated the performance of various models using four metrics: accuracy, precision, recall, and F1 score.
Results and ConclusionsThe results indicate that in stage Ⅲ, coals exhibited slightly increased values b and S and a decreased proportion of shear cracks. After entering stage Ⅳ, coals manifested opposite variation trends in value b and the proportion of shear cracks, along with significantly increased value S. With an increase in the loading rate, value b and its fluctuation amplitude decreased, value S showed a reduced increment, and the proportion of shear cracks exhibited a rising increment. The NRBO-XGBoost model enabled the intelligent identification of the crack propagation states of coals based on multivariate acoustic emission parameters. Compared to the XGBoost and PSO-XGBoost models, the NRBO-XGBoost model yielded higher accuracy, precision, recall, and F1 scores, which were 90.69%, 88.79%, 99.00%, and 93.62%, respectively under low loading rates and 82.76%, 86.76%, 88.50%, and 87.62%, respectively under high loading rates. The results of this study provide a novel philosophy for the identification and intelligent monitoring of the crack propagation states of coals using the acoustic emission technique. Establishing prediction models based on the measured acoustic emission data allows for the monitoring and early warning of dynamic hazards of coals.
-
煤岩体失稳破坏是大量复杂多样的裂纹叠加演化的结果，且不同程度的扰动作用、地质构造作用及外部荷载作用均会对煤岩体破坏产生不同的影响[1]。煤岩体破坏过程中所处的阶段能够反映其受压破坏状态，其中裂纹扩展阶段是裂纹扩展、贯通进而形成宏观裂纹的阶段，且处于煤岩体失稳破坏前，与煤矿开采的安全性密切相关。声发射信号中携带了煤岩体破坏过程中的诸多关键信息，以此判断煤岩稳定状态能够预测动力灾害的发生[2-4]。因此，基于煤岩破坏过程中的声发射特征准确识别其裂纹扩展状态，对研究煤岩失稳破坏至关重要。
目前，煤岩受压破坏状态与声发射信号特征的关联性是众多学者的研究重点。一些学者通过煤体破坏声发射试验及模型建立，发现煤岩加载塑性应变与声发射特征参数存在高度正相关关系[5]，声发射振铃计数和能量能很好地对应岩石破坏不同阶段，反映煤岩损伤演化过程[6-7]。部分学者依据声发射多元参量进行分析，煤岩受压破坏过程的声发射震级−频度关系b值“上升−波动−下降”的变化特征[8]，活跃度S值波动幅度与损伤阶段转变的对应[9]，均表明多元参量能有效反映煤岩破裂失稳过程。且基于声发射信号波形上升角斜率的倒数(RA)与平均频率(AF)的特征分析也可应用于煤岩破坏状态识别[10-11]。研究表明，煤岩声发射参数阶段性增长与加载速率正相关[12]，且加载速率影响下的声发射特性参数变化规律不同[13-14]。
目前关于煤岩破坏状态的识别多从应力关系及声发射物理量信息入手[15-18]，这种方法效率低、实时性不足，无法满足安全、高效及智能化开采的需要。近年来，随着人工智能的快速发展，一些学者结合声发射参数特征，利用支持向量机(SVM)、随机森林(RF)等机器学习算法，构建煤岩损伤状态识别模型[19]，实现对煤岩破坏状态的智能识别[20-21]。部分学者提取梅尔频率倒谱系数(MFCC)特征，利用BP神经网络、Light GBM等机器学习算法，有效识别应力状态的稳定性[22]，预测煤样的危险状态[23]。此外，还有学者结合声发射能级频次分布、波形频谱变化以及多分辨率融合等特征，利用SVM、集成学习等机器学习算法，对岩体破坏阶段进行智能辨识并预测岩体破坏[24-25]。这些研究表明了机器学习算法在煤岩裂纹扩展状态识别方面的可行性，推动了煤岩破坏状态识别方法的智能化发展。
综上，煤岩破坏状态的智能识别能够提高识别精度及效率，然而由于煤岩破坏过程复杂且受多种因素共同影响，在分析其阶段性破坏特征时，仅采用一种参数或少量几种参数的组合易遗漏重要信息，现有的识别方法尚未充分探讨声发射多元参量与煤岩破坏状态之间的关联性，且未深入探讨加载速率这一影响因素。
为此，构建NRBO(Newton-Raphson-based optimizer， 牛顿−拉夫逊优化算法)优化的XGBoost(eXtreme gradient boosting， 极限梯度提升算法)模型，分析声发射b、S及RA-AF值等多元参量与煤体裂纹扩展状态的对应关系，以不同加载速率下的声发射多元特征参量为训练样本，实现XGBoost参数自适应寻优，最终实现对煤体裂纹扩展状态的智能识别，以期为煤岩体破坏状态识别与智能监测研究提供一定的参考。
1 煤体破坏声发射监测试验
1.1 试样制备
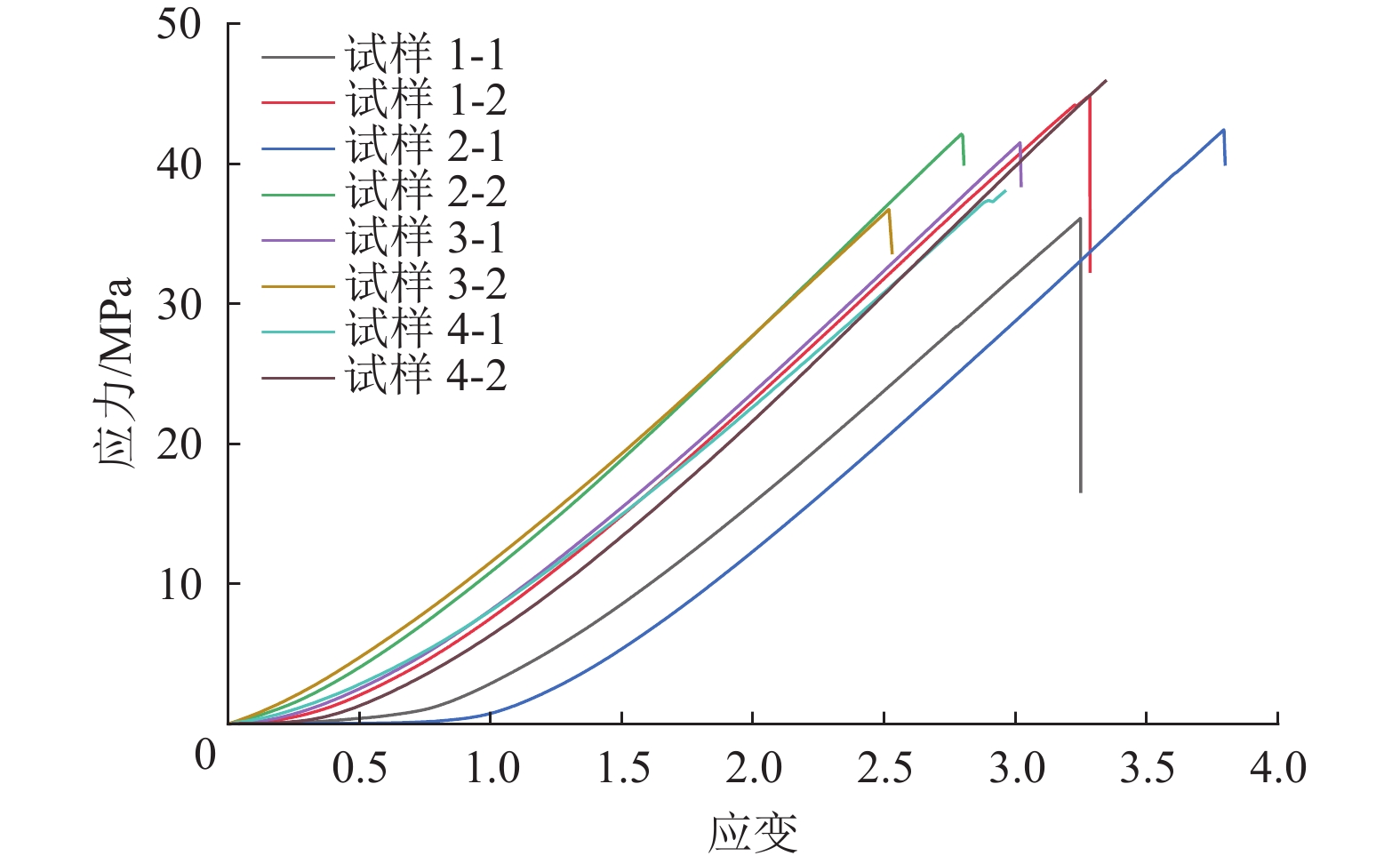
开展煤体破坏声发射监测试验，收集声发射数据，分析加载速率影响下煤体破坏过程的阶段性特征，并对煤体裂纹扩展状态进行识别。以2个试样为一组试验对象，采用1种加载速率。样品取自陕西神木市河畔煤矿，加工为标准圆柱体试样。试样共计8个，依次编号：1-1、1-2，2-1、2-2，3-1、3-2，4-1、4-2，试样抗压强度σ及加载速率v如图1所示。
不同加载速率下试样的应力−应变曲线如图2所示，可以获得各个试样在受压破坏过程中的应变情况。
煤是一种典型的非均质多孔介质材料，其内部原生裂隙网络分布差异性、矿物组分空间异质性及微观缺陷随机性等特性，使相同试验条件下试样的宏观力学响应存在必然的个体差异。此外，抗压强度存在偏差主要是因为：(1) 试样制备过程中不可控的端面平行度误差引起的应力集中差异；(2) 不同的层理构造与主裂隙走向的空间方位导致的破坏模式分化；(3) 孔隙率局部波动造成的有效承载面积变化。
后文建立的NRBO-XGBoost模型以声发射动态参数(b、S、RA-AF值等)而非静态力学参数作为输入集，这些参数本质是反映裂纹扩展过程中的能量释放模式与破裂机制。因此，即使试样宏观抗压强度存在波动，但各裂纹扩展阶段对应的声发射参数分布域具有显著可分性。通过标准化处理和滑动时间窗特征提取，能够有效消除试样个体差异对时序特征的影响，确保裂纹扩展阶段识别的鲁棒性。
1.2 试验系统及方案
煤体破坏声发射监测试验系统主要包括力学加载系统和声发射数据采集系统，如图3所示。力学加载系统为DNS200，能够同时记录时间、应力及应变等参数。声发射系统为Soundwel系列声发射信号采集仪，包括传感器、前置放大器、数据采集与处理系统。
![]()
图 3 单轴压缩声发射试验装置Figure 3. Experimental setup for acoustic emission under uniaxial compression其中传感器型号为SR150N，每个试样表面均布置2个传感器，用于收集加载过程中的声发射信号。此外，声发射监测仪采样频率为1 MHz，门槛值为40 dB。试样与声发射传感器之间涂抹凡士林以减少信号损失，并用电工胶带固定传感器以确保它与样品之间的良好接触。为了减少加载系统与其接触面摩擦噪声干扰，在试样上下面均涂抹凡士林。
试验开始前，检查各设备安装情况及传感器耦合程度。将试样放在加载平台上，预先加载 1~2 kN，使试样与加压板充分接触，避免试样与加压板接触时产生的噪声对声发射信号产生影响。煤体受压试验过程中，采用控制位移和应力2种方式进行加载，设定加载速率依次为0.1、0.3、0.6、1.0 mm/min。试验开始后，同步开启力学加载设备和声发射监测设备，采集力学和声发射试验数据，加载至试样破裂后试验结束。
2 煤体声发射多元参量阶段特征分析
由于煤体破坏过程复杂且影响因素多样，在分析阶段破坏特征时仅采用一种参数或少量几种参数的组合极易遗漏重要信息。因此结合b、S、RA和AF值这4个多元参量分析不同加载速率下煤体受压破坏过程的阶段性特征，能够更全面地反映煤体损伤破坏信息。试验得到4组加载速率下的结果，为使结果更具代表性和准确性，从中各挑选1个较为理想的试样的试验结果进行分析，即试样1-2、2-2、3-2、4-2，以这4个试样为代表，分别分析0.1、0.3、0.6、1.0 mm/min加载速率下的煤体受压破坏阶段性变化情况。
2.1 振铃计数与累计能量
声发射信号是煤岩体内部裂纹活动最直接的反映，其变化可以捕捉煤岩体应力状态，划分煤岩破坏阶段[26]。振铃计数和能量是最常用的声发射特征参数，振铃计数能反映声发射事件的活跃度和频率；能量可体现声发射信号中携带的能量信息，并反映煤体在破坏过程中的能量释放情况。基于声发射振铃计数与能量划分阶段的方法[27]，将试样1-2煤体破坏演化过程大致划分为4个阶段：压密阶段Ⅰ、弹性阶段Ⅱ、裂纹稳定扩展阶段Ⅲ和裂纹不稳定扩展阶段Ⅳ，如图4所示。
在阶段Ⅰ和Ⅱ，煤体内部的原生孔隙和裂隙被逐渐压密闭合，不足以产生新的裂纹，声发射信号较弱，振铃计数和能量均维持在较低水平，累计振铃计数和累计能量曲线基本一致，呈线性稳定增加趋势。在阶段Ⅲ，煤体声发射活动开始活跃，振铃计数开始增长，此时的累计振铃计数曲线增加趋势相较于前2个阶段变快，即斜率的增大趋势变得更显著。在阶段Ⅳ，煤体内部裂隙扩展、贯穿，形成较大裂纹，振铃计数急剧增长，累计振铃计数和累计能量均呈波浪式上涨趋势，煤体出现大面积破坏，荷载达到峰值应力后煤体崩裂，有明显的脆性破坏特征。
2.2 b值
声发射b值表示破裂震级和频度的关系，体现了不同尺度裂纹的发展趋势。常用最小二乘法和极大似然法拟合b值，最小二乘法简单易行但有一定的局限性，整体上极大似然法的效果更好，能有效避免大小震级权重不一致、样本量太少等问题，极大似然法拟合b值公式[28-29]为：
$$ b = \lg {{e}}/({m_{\text{a}}} - {m_{\min }}) $$ (1) 由图5可知，不同加载速率下煤体b值曲线整体呈现相似的波动递减趋势。加载初期的b值均处于较高水平，是由于煤体内部原生裂纹对应力变化的响应较为敏感。在压密阶段Ⅰ，原生裂纹逐渐闭合后，b值有小幅度波动减小趋势；在弹性阶段Ⅱ，声发射活动减弱，原生裂纹贯通的同时萌生次生裂纹，使得b值呈现波动状态；到达裂纹稳定扩展阶段Ⅲ后，不断积累的大量小裂纹使煤体产生大尺度裂纹，b值相较于前一阶段出现小幅度波动升高趋势；进入裂纹不稳定扩展阶段Ⅳ后，裂纹尺度不断增大，煤体内部损伤活动剧烈，不同尺度的裂缝逐渐贯通形成宏观裂缝面，b值低水平持续下降，煤体即将失稳破坏。
![]()
图 5 不同加载速率下煤体b值随时间阶段性变化Figure 5. Time variations of value b of coals in different failure stages under varying loading rates对比发现不同加载速率下煤体在Ⅲ和Ⅳ阶段的b值波动水平存在差异，0.1 mm/min时，b值在2.5水平波动，0.3和0.6 mm/min时，b值在2.25水平波动，1.0 mm/min时，b值在2.0水平波动，是因为加载速率增加导致应力集中与释放速率加快，微裂纹扩展更加连续，减少了因局部应力集中和突然释放而产生的强烈声发射信号。此外，0.1和0.3 mm/min下煤体b值在Ⅲ和Ⅳ阶段的波动幅度更大，随着加载速率的增加，b值变化幅度从超过0.5减小到不足0.5，表明低加载速率下煤体发生大尺度破裂更加彻底。
因此，可将b值作为煤体破坏前兆指标，其在阶段Ⅳ低水平持续下降时表示可能发生煤体失稳破坏。
2.3 S值
声发射活跃度S值将煤岩内部破裂时间、空间、强度因素考虑在内，包括声发射事件频次、平均能级、最大能级，能反映煤岩内部声发射源集中程度和能量尺度，由下式[30]计算得到：
$$ S = 0.117\lg (R + 1) + 0.029\lg \frac{{\displaystyle\sum\limits_{i = 1}^R {{{10}^{0.075{m_{{{{\mathrm{s}}i}}}}}}} }}{R} + 0.000\;75{m_{\max }} $$ (2) 由图6可知，不同加载速率下的声发射S值整体呈先减小后波动上升趋势。在压密阶段Ⅰ，随着原生裂纹的逐渐闭合，S值呈先升高后降低趋势；弹性阶段Ⅱ至裂纹不稳定扩展阶段Ⅳ，应力不断增大，煤体内部原生裂纹逐渐扩展、次生裂纹萌生并发育、颗粒间的摩擦以及大裂纹的贯通等原因导致声发射事件数不断增加，S值呈现长时间持续升高趋势。其中在进入阶段Ⅳ后，S值呈现高水平持续升高趋势，在峰值应力时达到最大值，煤体即将失稳破坏。在第Ⅳ阶段的增加幅度相较于第Ⅲ阶段更显著，且随着加载速率的增加，第Ⅲ阶段的S值增加幅度减小。
![]()
图 6 不同加载速率下煤体S值随时间阶段性变化Figure 6. Time variations of value S of coals in different failure stages under varying loading rates对比发现不同加载速率下煤体在Ⅲ和Ⅳ阶段的S值演化特征差异明显。随着加载速率的增加，2个阶段的增加幅度减小，0.1和0.3 mm/min下的S值增加幅度均在0.23以上，0.6和1.0 mm/min下的S值增加幅度均在0.17以下，是因为加载速率的增加使应力在较短的时间内释放，减少了声发射活动的持续时间和强度。
因此，可将S值作为煤体破坏前兆指标，其在阶段Ⅳ高水平持续升高时表示可能发生煤体失稳破坏。
2.4 RA-AF值
AF和RA值分别表示声发射信号的平均频率和波形上升角斜率的倒数，其中RA值为事件上升时间与幅值的比值，AF值为振铃计数与持续时间的比值[8]。如图7所示，虚斜线上的数字为数据点分布在斜线上下区域所占的比例，当RA值相对较大、AF值相对较小(图7斜虚线以下部分)时表现为剪切裂纹，反之为张拉裂纹。
![]()
图 7 不同加载速率下煤体RA-AF值阶段性变化Figure 7. RA vs. AF of coals in different failure stages under varying loading rates由图7可知，煤体在不同加载速率下各个阶段的RA-AF值分布存在相似之处。在煤体破坏过程中，压密阶段Ⅰ至裂纹稳定扩展阶段Ⅲ的张拉裂纹逐渐增加，进入裂纹不稳定扩展阶段Ⅳ后，张拉裂纹减少，是因为阶段Ⅲ下煤体内部受拉应力作用产生大量新的张拉裂纹，阶段Ⅳ下宏观裂纹的迅速扩展和相互连接导致已存在的裂纹网络占据主导地位，新裂纹的产生对张拉裂纹总占比的贡献减小。且在峰值应力前，剪切裂纹的比例开始显著增加。
对比发现不同加载速率下煤体在Ⅲ和Ⅳ阶段的RA-AF分布具有明显差异。随着加载速率的增加，煤体在Ⅲ至Ⅳ阶段时剪切裂纹所占的比例增加幅度逐渐增大，即5.01%~8.45%，表明加载速率的增加可以形成更多的剪切裂纹。
因此，可将RA-AF值作为煤体破坏前兆指标，Ⅰ至Ⅲ阶段整体趋势为剪切裂纹所占比例逐渐减小，进入Ⅳ阶段后变为相反趋势时，煤体可能发生失稳破坏。
3 煤体裂纹扩展状态智能识别
3.1 数据集
根据对b、S、RA、AF值的统计分析发现，可以将它们作为煤体破坏失稳的前兆指标，且煤体的裂纹稳定扩展阶段和不稳定扩展阶段在一定程度上代表着煤体破裂前大裂纹的产生和贯通过程，这2个阶段的数据对于研究煤体失稳破坏更具代表性，因此，煤体破坏过程声发射多元参量和所处的破坏阶段分别是样本数据集的特征和对应标签。
有效值电压(RMS)提供了信号的强度平均值，平均信号电平(ASL)是信号电平的平均值。由图8可知，4个多元参量与ASL和RMS特征参数无直接关系，因此，引入二者以扩充数据集。由于不同加载速率下的煤体破坏过程中每秒收集到的声发射特征参数数据量不同，所以在计算多元参量数据时，为了保证统计窗口内数据量差别不大，根据在0.1、0.3、0.6和1.0 mm/min加载速率下煤体破坏的实际数据量情况，分别以0.8、0.4、0.2和0.2 s为统计时窗，其中AF、RA、ASL、RMS值取统计时窗内的平均值。
为研究加载速率影响下的模型智能识别效果，将在0.1和0.3 mm/min、0.6和1.0 mm/min下的数据分别作为低、高加载速率样本。每组样本数据量均为
1450 个，其中处于裂纹稳定扩展阶段和不稳定扩展阶段的样本数据量分别为1000 和450个。处于裂纹稳定扩展阶段的样本数据标签为“1”，处于裂纹不稳定扩展阶段的样本数据标签为“2”，即分别代表裂纹稳定扩展状态和裂纹不稳定扩展状态。打乱数据集，训练集与测试集数量比例为8∶2，将高低加载速率下的煤体样本数据依次输入模型中。由于采集到的声发射信号样本各特征具有一定的分布维度差异，为了消除这些差异对识别结果的影响，对样本数据进行最大最小归一化处理[8]，将原始数据标定到[0,1]，使不同样本之间的数据具有可比性。最大最小归一化表达式如下：$$ {x^*} = \frac{{{x_{\mathrm{t}}} - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} $$ (3) 3.2 NRBO-XGBoost模型智能识别方法
基于煤体破坏过程声发射信号的裂纹扩展状态智能识别的核心在于声发射信号与裂纹扩展状态之间的关联性，对于不同加载速率下的煤体破坏声发射数据的差异，NRBO能够通过迭代寻找XGBoost的最优参数设置，实现XGBoost参数自适应寻优，从而在不同加载速率下数据集上最大化模型的性能。因此，融合这2种算法构建NRBO-XGBoost模型，能够更精确地对煤体裂纹扩展状态进行智能识别与分类。
3.2.1 XGBoost算法
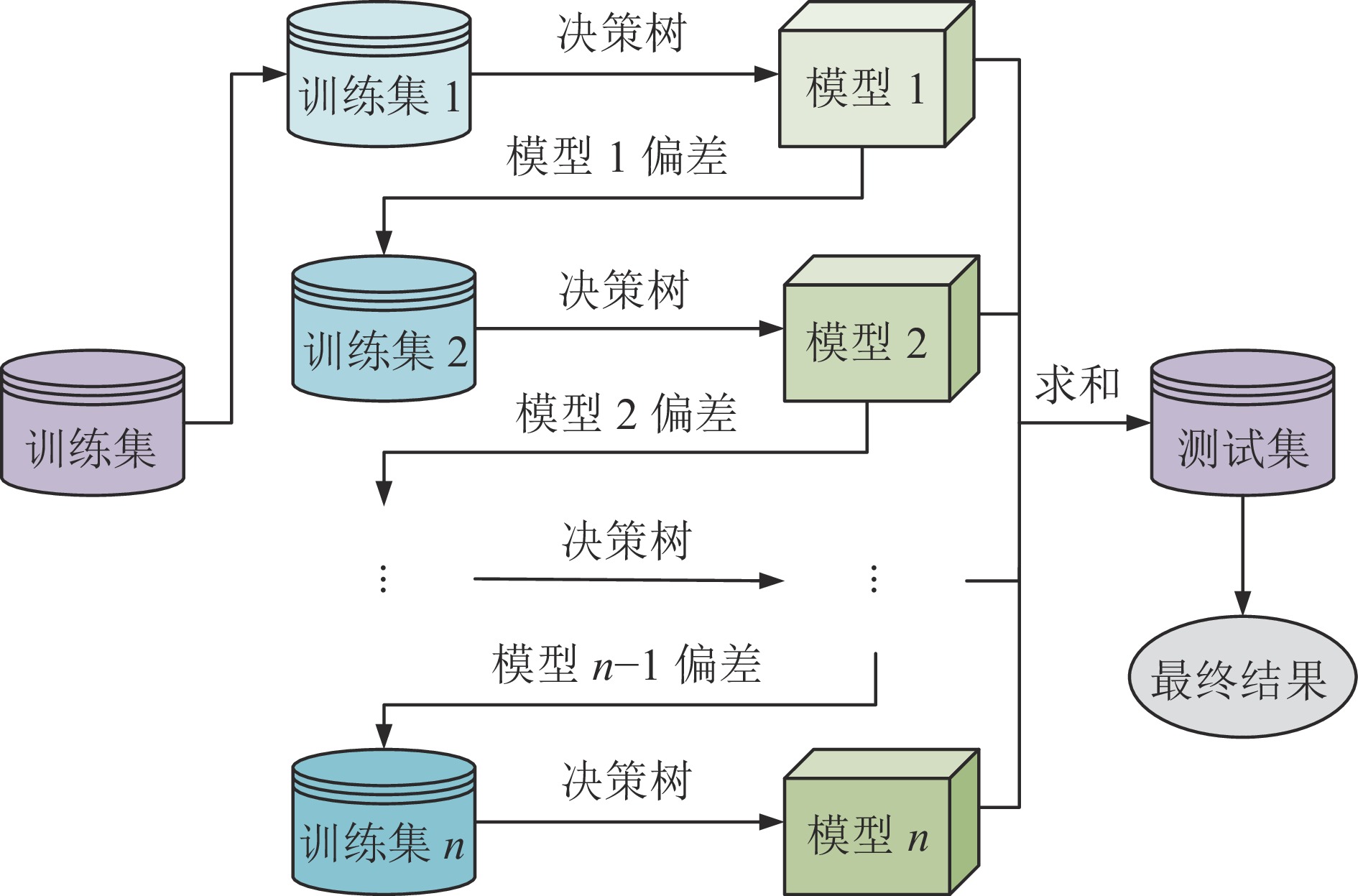
XGBoost是梯度提升决策树算法的一种高效实现。其基础模型是决策树，核心是Boosting思想，由多个决策树共同决策，后一棵决策树生成时将之前所有树的偏差考虑在内，以提升整个模型效果。XGBoost原理如图9所示。
XGBoost的目标函数由损失函数和正则化项组成[31]，目标是最小化损失函数并控制模型的复杂度。目标函数表达式如下：
$$ \varphi = \sum\limits_{j = 1}^M {l({y_j},{y_{j1}})} + \sum\limits_{k = 1}^K {\varOmega ({f_k})} $$ (4) 损失函数用以比较模型预测值与真实值之间差异，XGBoost常用对数损失函数处理二分类问题。正则化项能防止过拟合，控制模型复杂度。正则化项由2部分组成，表达式如下：
$$ \varOmega (f) = \gamma {{E}} + \frac{1}{2}\lambda \sum\limits_{h = 1}^E {w_h^2} $$ (5) 3.2.2 NRBO算法
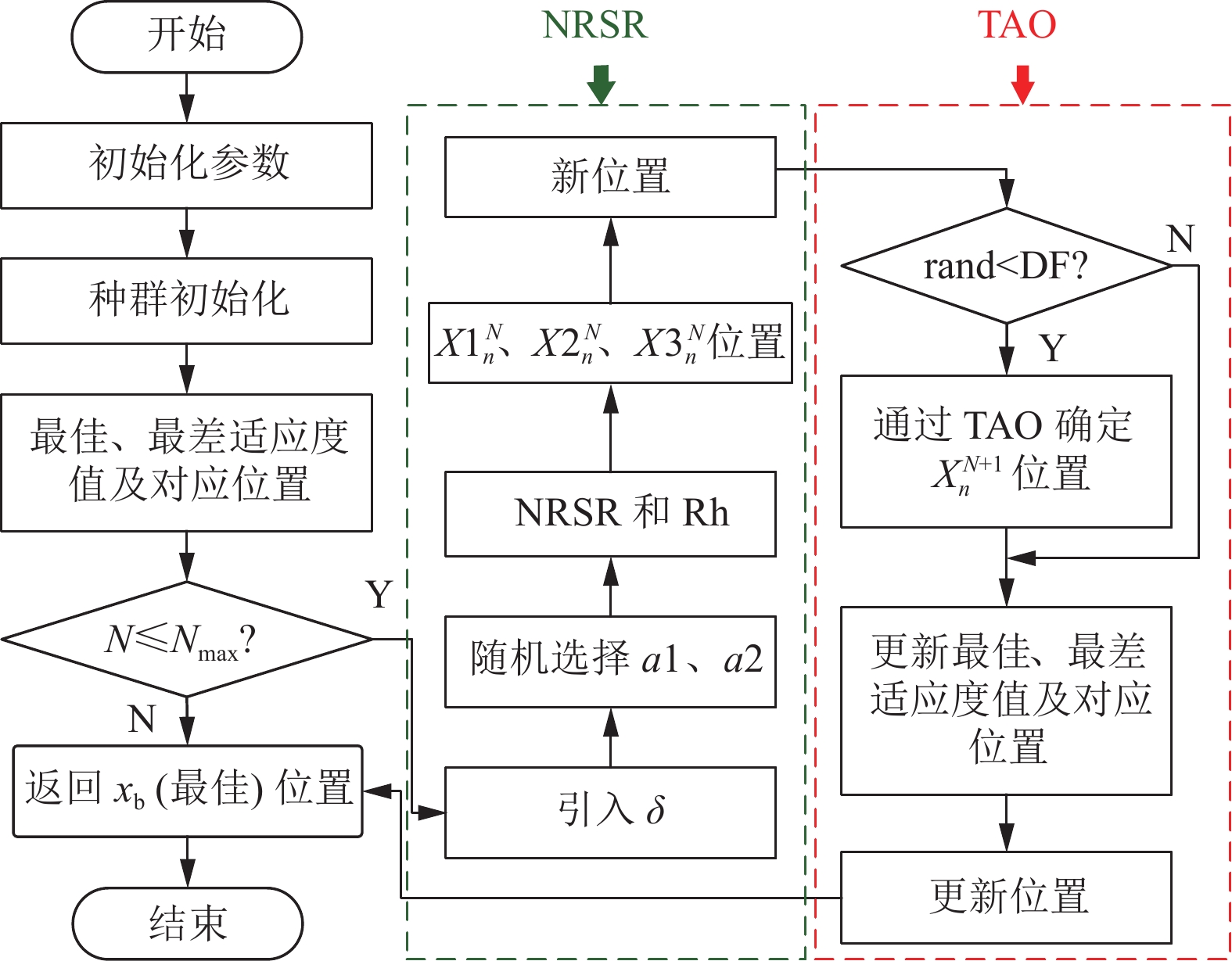
牛顿−拉夫逊法(Newton-Raphson Method，NRM)是一种寻找方程根的方法。NRBO是受NRM启发，由S. Ravichandran等[32]在2024年提出的一种新的元启发式优化算法。该方法采用了Newton-Raphson搜索规则(NRSR)来增强NRBO的探索能力，并加快收敛速度，还引入了陷阱避免算子(TAO)改变解的更新方式，增加随机性和多样性，从而避免局部最优陷阱。
1) Newton-Raphson搜索规则(NRSR)
利用NRSR规则探索新的解。对于第N次迭代中第n个个体，用NRSR探索个体位置，新位置表达式：
$$ x_n^{N + 1} = {r_1}[{r_1}X1_n^N + (1 - {r_1})X2_n^N] + (1 - {r_1})X3_n^N $$ (6) $X1_n^N $、$X2_n^N $、$X3_n^N $表达式依次为：
$$ X1_n^N = x_n^N - {\mathrm{Nt}} + {\mathrm{Rh}} $$ (7) $$ X2_n^N = {x_{\mathrm{b}}} - {\mathrm{Nt}} + {\mathrm{Rh}} $$ (8) $$ X3_n^N = x_n^N - \delta (X2_n^N - X1_n^N) $$ (9) Nt、Rh、δ的表达式如下：
$$ {\text{Nt}} = {\mathrm{randn}} \times \frac{{({y_{\mathrm{c}}} - {y_{\mathrm{d}}})\Delta x}}{{2({y_{\mathrm{c}}} + {y_{\mathrm{d}}} - 2x_n^N)}} $$ (10) $$ {\mathrm{Rh}} = c({x_{\mathrm{b}}} - x_n^N) + g(x_{{\mathrm{a}}1}^N - x_{{\mathrm{a}}2}^N) $$ (11) $$ \delta =\left(1-\frac{2N}{{N}_{\mathrm{max}}}\right)^{5} $$ (12) $$ \Delta x = {\mathrm{rand}}(1,{\mathrm{dim}})\left| {{x_{\mathrm{b}}} - x_n^N} \right| $$ (13) 2) 陷阱规避操作(TAO)
当检测到陷入局部最优时，TAO通过结合最优位置和当前位置来找到更优的解$x_{\mathrm{TAO}}^N $，以解决此问题。产生新的值$x_{\mathrm{TAO}}^N $表达式如下：
$$ x_n^{N + 1} = x_{{\mathrm{TAO}}}^N,\quad {\mathrm{rand}} < {\mathrm{DF}} $$ (14) $$ \left\{\begin{aligned} & x_{{\mathrm{TAO}}}^N = x_n^{N + 1} + {\theta _1}({\mu _1}{x_{\mathrm{b}}} - {\mu _2}x_n^N) + \\ &\qquad{\theta _2}\delta [{\mu _1}{\mathrm{Mean}}({x^N} - {\mu _2}x_n^N)],\quad{\text{if }}\;{\mu _1} < 0.5 \\ & x_{{\mathrm{TAO}}}^N = {x_{\mathrm{b}}} + {\theta _1}({\mu _1}{x_{\mathrm{b}}} - {\mu _2}x_n^N) + \\ &\qquad {\theta _2}\delta [{\mu _1}{\mathrm{Mean}}({x^N} - {\mu _2}x_n^N)],\quad{\text{if }}\;{\mu _1} \geqslant 0.5 \\ \end{aligned} \right. $$ (15) μ1和μ2按照下式计算：
$$ \left\{\begin{aligned} & {{\mu _1} = 3\;{\mathrm{rand}} \times \beta + (1 - \beta )} \\ & {{\mu _2} = {\mathrm{rand}} \times \beta + (1 - \beta )} \end{aligned} \right. $$ (16) NRBO算法整体流程如图10所示。
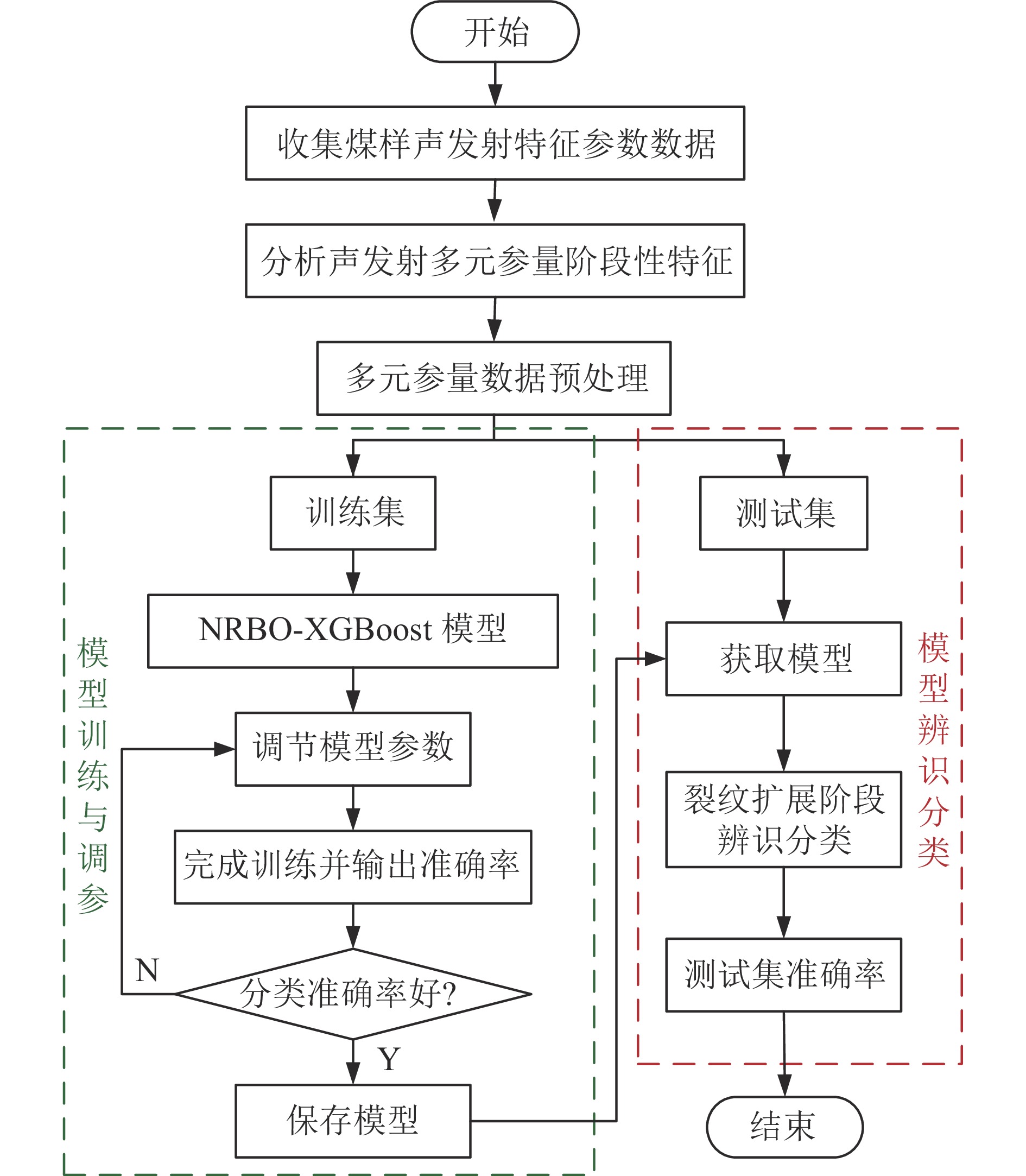
3.2.3 模型智能识别流程
在Matlab软件平台上利用NRBO-XGBoost模型对煤体裂纹扩展状态进行智能识别分类的具体流程如图11所示。
![]()
图 11 NRBO-XGBoost模型识别流程Figure 11. Flow chart showing the identification of the NRBO-XGBoost model(1) 将收集的声发射特征参数数据处理为多元参量并分析阶段性特征，之后进行筛选和预处理，并按8∶2的比例将数据划分训练集和测试集。
(2) 编译NRBO-XGBoost网络模型。
(3) 反复对模型进行调参，确定最优参数。
(4) 将测试集输入到调优后保存的模型中，对裂纹扩展阶段进行智能识别分类，评估模型性能。
3.2.4 模型参数
NRBO-XGBoost模型参数见表1，其中优化目标参数主要包括：最大训练次数、树的深度和学习率。
表 1 NRBO-XGBoost模型参数Table 1. Parameters of the NRBO-XGBoost model参数 数值 优化参数(最大训练次数、树的深度和
学习率)目标下限[100,3, 0.0001 ]优化参数(最大训练次数、树的深度和
学习率)目标上限[ 1000 ,10,0.1]种群数量 20 最大迭代次数 20 TAO决定因素 0.6 3.3 加载速率影响下模型智能识别结果分析
3.3.1 模型适应度
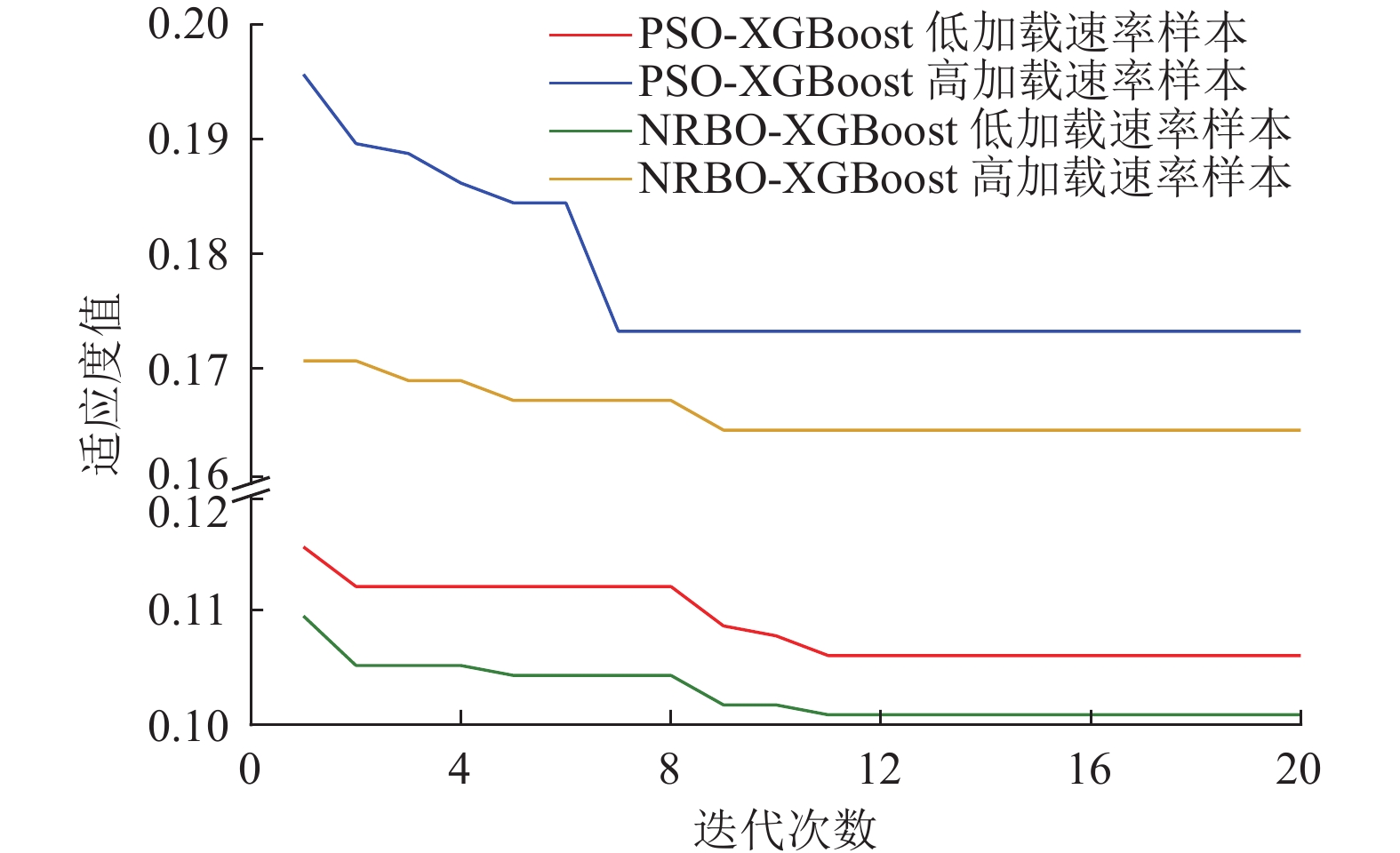
适应度值是衡量模型在当前迭代步骤中表现好坏的指标，常用于优化算法中，该值越小，表明训练效果越好，模型精度越高。为了研究加载速率影响下NRBO-XGBoost模型的最优适应度变化，并凸显其优越性，与引入粒子群算法(PSO)优化的XGBoost模型作对比，绘制了PSO-XGBoost模型和NRBO-XGBoost模型的适应度变化曲线，如图12所示。
![]()
图 12 高低加载速率下PSO/NRBO-XGBoost模型适应度变化曲线Figure 12. Fitness curves of PSO/NRBO-XGBoost models under high and low loading rates由图12可知，迭代周期内，种群整体向最优适应度值逐渐移动。就寻优效率而言，对于PSO-XGBoost模型，低和高加载速率下迭代次数分别为11和7时，最优适应度值趋于稳定；对于NRBO-XGBoost模型，低和高加载速率下迭代次数分别为11和9时，最优适应度值趋于稳定。表明在同一模型下，两者均对高加载速率样本寻优效率稍快；在不同模型下，两者对高或低加载速率样本的寻优效率相差不大。
就适应度值而言，对于PSO-XGBoost模型，低和高加载速率样本下适应度值分别为0.106和0.173；对于NRBO-XGBoost模型，低和高加载速率样本下适应度值分别为
0.1008 和0.1646 。表明在同一模型下，两者均对低加载速率样本的适应度值更低；在不同模型下，NRBO-XGBoost模型对高或低加载速率样本的适应度值均较低，说明该模型对样本的适应效果更好。NRBO-XGBoost模型更适用于低加载速率受压煤体裂纹扩展状态识别的原因是：在高加载速率下，煤体破坏过程更加迅速、剧烈，声发射信号在短时间内快速增强并达到峰值，能量释放和应力分布不均匀且难以预测，导致声发射信号在时间和空间上的分布更加复杂，使得模型不易准确捕捉到裂纹扩展过程中的关键特征。且高加载速率下的训练数据质量较低(如噪声较多、数据不完整等)，影响模型的训练效果和最终性能。这些原因导致特征提取和模型学习难度增大，使得模型在高加载速率下的适应效果下降。而在低加载速率下，煤体破坏过程相对平稳，裂纹扩展过程更加有序，阶段之间的过渡更加清晰，且噪声和干扰相对较少，使得模型更适合低加载速率下的数据。
3.3.2 模型性能对比
利用测试集验证模型的性能，将准确率、精确率、召回率及F1值作为模型性能的评价指标[33]，对结果进行统计分析，各模型分类性能对比见表2。
表 2 各模型分类性能对比Table 2. Comparison of classification performance among various models分类模型 准确率/% 精确率/% 召回率/% F1分数 低速率 高速率 低速率 高速率 低速率 高速率 低速率 高速率 XGBoost 84.83 76.63 84.82 80.69 95 84.9 89.62 83.74 PSO-XGBoost 88.97 80.69 84.29 82.41 95 88.4 92.23 86.34 NRBO-XGBoost 90.69 82.76 88.79 86.76 99 88.5 93.62 87.62 由表2可知，在同一模型下，低加载速率样本下4个评价指标值均较高，即智能识别效果更好；在不同模型下，NRBO-XGBoost模型的4个指标值均比PSO-XGBoost模型和XGBoost模型更高，即该模型性能更优，说明NRBO对XGBoost算法的优化效果更显著。就NRBO-XGBoost模型而言，对于准确率、精确率、召回率和F1值4个指标，低加载速率样本下比另外2个模型依次分别高1.72%和5.86%、4.50%和3.97%、4.00%和4.00%、1.39%和4.00%，高加载速率样本下比另外2个模型依次分别高2.07%和6.13%、4.35%和6.07%、0.10%和3.60%、1.28%和3.88%。说明利用NRBO对XGBoost模型进行优化，显著提高了模型的分类性能。因此，NRBO-XGBoost模型对煤体裂纹扩展状态识别的4项评估指标均最高，具有良好的性能，且对低加载速率受压煤体裂纹扩展状态的识别效果更好。
NRBO-XGBoost模型对不同加载速率受压煤体的裂纹扩展状态识别性能有差异的原因是：煤体受压的加载速率变化导致其内部应力状态和破坏模式发生变化，影响声发射信号的强度、频率等特征，进而计算得到的多元声发射参量数据也会因此改变。以多元参量数据作为数据集，输入到NRBO-XGBoost模型中，数据集的变化会影响NRBO自适应参数寻优的结果，最后使得模型识别的效果发生改变，即该模型对高和低加载速率受压煤体的裂纹扩展阶段声发射数据的识别准确率、精确率等评估指标值差异较大。进一步可解释该模型对低加载速率受压煤体的裂纹扩展状态识别性能更好的原因是：煤体在低加载速率受压时，裂纹扩展过程更为缓慢且渐进，声发射信号的特征变化更为规律，使多元声发射参量更为稳定且易于分析，将其输入到NRBO-XGBoost模型时，NRBO自适应参数寻优机制在平稳的数据集下更易找到最优参数组合，且该模型在训练过程中能够更准确学习到这些特征与裂纹扩展阶段之间的映射关系。
4 结 论
(1) 构建了NRBO-XGBoost模型，利用该模型能够对不同加载速率下煤体声发射多元参量数据的XGBoost参数进行自适应寻优，更精确地实现裂纹扩展状态的智能识别。
(2) 与PSO-XGBoost和XGBoost模型相比，构建的NRBO-XGBoost模型性能更优，能够减少重要信息的遗漏，应用于低和高加载速率下，样本准确率分别达到90.69%和82.76%，表明该模型更适合低加载速率样本。
(3) 建立的NRBO-XGBoost模型为声发射技术在煤体裂纹扩展状态识别与智能监测研究提供了新的思路。可进一步利用实测声发射数据建立预测模型，对煤岩动力灾害进行监测、预警。
符号注释：
DF为控制NRBO性能的决定因素；c为(0,1)之间的随机数；E为叶节点数量；fk为第k棵树的预测函数；g为(0,1)之间的随机数；K为树的数量；l(yj,yj1)为损失函数，表示对第j个观察值的预测偏差；ma为平均震级；msi为第i事件幅值的震级$i=1,2,\cdots,R $；mmax为统计窗口最大事件幅值的震级；mmin为最小震级，为声发射幅值的1/20；M为数据量；n为个体序号，不大于种群个体数量；N为当前迭代次数；Nmax为最大迭代次数；Nt为应用NRSR搜索规则所得到的值；r1为(0,1)的随机数；rand为种群初始化中用到的随机数的函数，在(0,1)范围；rand(1,dim)为具有dim维度决策变量的随机数；randn为均值为0、方差为1的正态分布随机数；R为统计时间段内事件总数(i=1,2,···,R)；Rh为将种群引向正确方向的一个步长因子；wh为第h个叶节点的权重(h=1,2,···,E)；xb为当前最佳位置；xt、x*分别为样本数据处理前后的值；xmin、xmax分别为样本数据最大、最小值；$x_n^N $为当前位置；$x_n^{N+1} $为应用NRSR规则探索的新位置；$x_{a1}^N $、$x_{a2}^N $分别为第a1、a2个个体的位置；∆x为探索的范围；$X1_n^N $、$X2_n^N $、$X3_n^N $分别为NRBO更新得到的3个位置；yc、yd分别为应用 NRSR搜索规则结果生成的两个位置；yj、yj1分别为第j个观察值的真实标签和预测标签；β为二进制数，即1或0，如果∆x≥0.5，β值为0，否则为1；γ、λ均为正则化参数；δ为随迭代次数变化的自适应系数；θ1、θ2分别为(−1,1)和(−0.5,0.5)之间的随机数；μ1和μ2均为随机数；Ω(f)为模型复杂度；Ω(fk)为第k棵树的复杂度(因子正则化，防止模型过拟合)；φ为目标函数。
-
![]()
图 3 单轴压缩声发射试验装置
Fig. 3 Experimental setup for acoustic emission under uniaxial compression
![]()
图 5 不同加载速率下煤体b值随时间阶段性变化
Fig. 5 Time variations of value b of coals in different failure stages under varying loading rates
![]()
图 6 不同加载速率下煤体S值随时间阶段性变化
Fig. 6 Time variations of value S of coals in different failure stages under varying loading rates
![]()
图 7 不同加载速率下煤体RA-AF值阶段性变化
Fig. 7 RA vs. AF of coals in different failure stages under varying loading rates
![]()
图 11 NRBO-XGBoost模型识别流程
Fig. 11 Flow chart showing the identification of the NRBO-XGBoost model
![]()
图 12 高低加载速率下PSO/NRBO-XGBoost模型适应度变化曲线
Fig. 12 Fitness curves of PSO/NRBO-XGBoost models under high and low loading rates
表 1 NRBO-XGBoost模型参数
Table 1 Parameters of the NRBO-XGBoost model
参数 数值 优化参数(最大训练次数、树的深度和
学习率)目标下限[100,3, 0.0001 ]优化参数(最大训练次数、树的深度和
学习率)目标上限[ 1000 ,10,0.1]种群数量 20 最大迭代次数 20 TAO决定因素 0.6 
下载: 导出CSV
表 2 各模型分类性能对比
Table 2 Comparison of classification performance among various models
分类模型 准确率/% 精确率/% 召回率/% F1分数 低速率 高速率 低速率 高速率 低速率 高速率 低速率 高速率 XGBoost 84.83 76.63 84.82 80.69 95 84.9 89.62 83.74 PSO-XGBoost 88.97 80.69 84.29 82.41 95 88.4 92.23 86.34 NRBO-XGBoost 90.69 82.76 88.79 86.76 99 88.5 93.62 87.62
下载: 导出CSV
-
[1] 康玉梅,谷今,魏梦琦. 不同加载速率下软硬互层类岩石力学及声发射特性[J]. 东北大学学报(自然科学版),2023,44(3):399−407. DOI: 10.12068/j.issn.1005-3026.2023.03.013 KANG Yumei,GU Jin,WEI Mengqi. Mechanical properties and acoustic emission characteristics of soft–hard interbedded rocks under different loading rates[J]. Journal of Northeastern University (Natural Science),2023,44(3):399−407. DOI: 10.12068/j.issn.1005-3026.2023.03.013
[2] 周露林,刘建锋,鲁功达,等. 热损伤花岗岩三轴压缩蠕变破坏声发射及损伤演化特征[J]. 中南大学学报(自然科学版),2023,54(6):2360−2369. ZHOU Lulin,LIU Jianfeng,LU Gongda,et al. Creep acoustic emission and damage evolution of thermally–damaged granite under triaxial stress[J]. Journal of Central South University (Science and Technology),2023,54(6):2360−2369.
[3] 纪洪广,张春瑞,张月征,等. 岩石材料破裂过程中声发射信号的应力状态及能量演化研究[J]. 中国矿业大学学报,2024,53(2):211−223. JI Hongguang,ZHANG Chunrui,ZHANG Yuezheng,et al. Research on stress state and energy evolution of acoustic emission signal during rock materials fracture process[J]. Journal of China University of Mining & Technology,2024,53(2):211−223.
[4] PENG Kang,ZHOU Jiaqi,ZOU Quanle,et al. Deformation characteristics and failure modes of sandstones under discontinuous multi–level cyclic loads[J]. Powder Technology,2020,373:599−613.
[5] JIN Peijian,WANG Enyuan,SONG Dazhao. Study on correlation of acoustic emission and plastic strain based on coal–rock damage theory[J]. Geomechanics and Engineering,2017,12(4):627−637.
[6] 孙雪,李二兵,段建立,等. 北山花岗岩三轴压缩下声发射特征及损伤演化规律研究[J]. 岩石力学与工程学报,2018,37(增刊2):4234−4244. SUN Xue,LI Erbing,DUAN Jianli,et al. Study on acoustic emission characteristics and damage evolution law of Beishan granite under triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering,2018,37(Sup.2):4234−4244.
[7] 李明,浦海,陈彦龙,等. 压剪复合载荷下煤岩蠕变力学特性及声发射特征[J]. 采矿与安全工程学报,2024,41(4):801−812. LI Ming,PU Hai,CHEN Yanlong,et al. Creep mechanical properties and acoustic emission characteristics of coal and rock under compressive shear combined load[J]. Journal of Mining & Safety Engineering,2024,41(4):801−812.
[8] 胡千庭,刘荣辉,李全贵,等. 单轴压缩下典型煤岩破坏的声发射特征研究[J]. 地下空间与工程学报,2023,19(6):1769−1781. HU Qianting,LIU Ronghui,LI Quangui,et al. Acoustic emission characteristics study of typical coal rock failure under uniaxial compression[J]. Chinese Journal of Underground Space and Engineering,2023,19(6):1769−1781.
[9] 张凯,张东晓,赵勇强,等. 损伤岩石声发射演化特征及响应机制试验研究[J]. 煤田地质与勘探,2024,52(3):96−106. DOI: 10.12363/issn.1001-1986.23.09.0548 ZHANG Kai,ZHANG Dongxiao,ZHAO Yongqiang,et al. Experimental study on acoustic emission evolution characteristics and response mechanism of damaged rocks[J]. Coal Geology & Exploration,2024,52(3):96−106. DOI: 10.12363/issn.1001-1986.23.09.0548
[10] DU Kun,LI Xuefeng,TAO Ming,et al. Experimental study on acoustic emission (AE) characteristics and crack classification during rock fracture in several basic lab tests[J]. International Journal of Rock Mechanics and Mining Sciences,2020,133:104411.
[11] DONG Longjun,CHEN Yongchao,SUN Daoyuan,et al. Implications for rock instability precursors and principal stress direction from rock acoustic experiments[J]. International Journal of Mining Science and Technology,2021,31(5):789−798.
[12] 张泽坤,宋战平,程昀,等. 加载速率影响下类硬岩声发射及破裂响应特征[J]. 煤田地质与勘探,2022,50(2):115−124. ZHANG Zekun,SONG Zhanping,CHENG Yun,et al. Acoustic emission characteristics and fracture response behavior of hard rock–like material under influence of loading rate[J]. Coal Geology & Exploration,2022,50(2):115−124.
[13] HU Shihong,SU Guoshao,QIN Yuanzhuo,et al. Influence of the loading rate on the evolution characteristics of AE and MS signals during granite failure[J]. Engineering Failure Analysis,2023,152:107428.
[14] LIU Guokun,WANG Wenxi,LI Xiaohua,et al. Analysis of the effect of loading rate on mechanical properties of fissured rock materials and acoustic emission characteristic parameters[J]. Buildings,2024,14(6):1579.
[15] 曾鹏,刘阳军,纪洪广,等. 单轴压缩下粗砂岩临界破坏的多频段声发射耦合判据和前兆识别特征[J]. 岩土工程学报,2017,39(3):509−517. DOI: 10.11779/CJGE201703015 ZENG Peng,LIU Yangjun,JI Hongguang,et al. Coupling criteria and precursor identification characteristics of multi–band acoustic emission of gritstone fracture under uniaxial compression[J]. Chinese Journal of Geotechnical Engineering,2017,39(3):509−517. DOI: 10.11779/CJGE201703015
[16] 姚旭龙,张艳博,刘祥鑫,等. 岩石破裂声发射关键特征信号优选方法[J]. 岩土力学,2018,39(1):375−384. YAO Xulong,ZHANG Yanbo,LIU Xiangxin,et al. Optimization method for key characteristic signal of acoustic emission in rock fracture[J]. Rock and Soil Mechanics,2018,39(1):375−384.
[17] 冯龙飞,王皓,王晓东,等. 煤冲击破坏的微破裂演化特征及前兆识别[J]. 岩石力学与工程学报,2022,41(7):1440−1452. FENG Longfei,WANG Hao,WANG Xiaodong,et al. Microfracture evolution characteristics and precursor identification of coal impact failure[J]. Chinese Journal of Rock Mechanics and Engineering,2022,41(7):1440−1452.
[18] 邓绪彪,王新月,孙本利,等. 基于声发射波形能量谱的岩石裂隙演化研究[J]. 矿业安全与环保,2024,51(1):127−132. DENG Xubiao,WANG Xinyue,SUN Benli,et al. Investigation on evolution of rock fractures based on acoustic emission by waveform energy spectrum[J]. Mining Safety & Environmental Protection,2024,51(1):127−132.
[19] 隆能增,任松,吴斐,等. 酸性干湿循环下泥质砂岩劣化及声发射演化特征识别研究[J]. 岩土力学,2024,45(9):2653−2668. LONG Nengzeng,REN Song,WU Fei,et al. Degradation of argillaceous sandstone and identification of acoustic emission evolution characteristics under acidic wet–dry cycles[J]. Rock and Soil Mechanics,2024,45(9):2653−2668.
[20] 赵云阁,黄麟淇,李夕兵. 岩石损伤强度及峰值强度前后阶段的声发射识别[J]. 岩土工程学报,2022,44(10):1908−1916. ZHAO Yunge,HUANG Linqi,LI Xibing. Identification of stages before and after damage strength and peak strength using acoustic emission tests[J]. Chinese Journal of Geotechnical Engineering,2022,44(10):1908−1916.
[21] 刘剑,周宗红,张晶,等. 闪长岩不同卸荷速率声发射特征及非稳定阶段识别[J]. 岩土力学,2025,46(1):225−232. LIU Jian,ZHOU Zonghong,ZHANG Jing,et al. Acoustic emission characteristics of diorite at varying unloading rates and identification of its unsteady phases[J]. Rock and Soil Mechanics,2025,46(1):225−232.
[22] DING Ziwei,LI Xiaofeng,HUANG Xing,et al. Feature extraction,recognition,and classification of acoustic emission waveform signal of coal rock sample under uniaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences,2022,160:105262. DOI: 10.1016/j.ijrmms.2022.105262
[23] 李振雷,李娜,杨菲,等. 基于声发射特征提取和机器学习的煤破坏状态预测[J]. 工程科学学报,2023,45(1):19−30. LI Zhenlei,LI Na,YANG Fei,et al. Applying feature extraction of acoustic emission and machine learning for coal failure forecasting[J]. Chinese Journal of Engineering,2023,45(1):19−30.
[24] LI Jing,YUE Jianhua,YANG Yong,et al. Multi–resolution feature fusion model for coal rock burst hazard recognition based on Acoustic Emission data[J]. Measurement,2017,100:329−336. DOI: 10.1016/j.measurement.2017.01.010
[25] 董陇军,张义涵,孙道元,等. 花岗岩破裂的声发射阶段特征及裂纹不稳定扩展状态识别[J]. 岩石力学与工程学报,2022,41(1):120−131. DONG Longjun,ZHANG Yihan,SUN Daoyuan,et al. Stage characteristics of acoustic emission and identification of unstable crack state for granite fractures[J]. Chinese Journal of Rock Mechanics and Engineering,2022,41(1):120−131.
[26] WU Chen,GONG Fengqiang,LUO Yong. A new quantitative method to identify the crack damage stress of rock using AE detection parameters[J]. Bulletin of Engineering Geology and the Environment,2021,80(1):519−531. DOI: 10.1007/s10064-020-01932-6
[27] 朱贵旺,秦磊,丁蔚健,等. 基于声发射参数的超材料对水泥基材料弯曲韧性影响研究[J]. 硅酸盐通报,2025,44(2):424−433. ZHU Guiwang,QIN Lei,DING Weijian,et al. Influences of metamaterials on bending toughness of cement–based materials based on acoustic emission parameters[J]. Bulletin of the Chinese Ceramic Society,2025,44(2):424−433.
[28] 吴果,周庆,冉洪流. 震级–频度关系中b值的极大似然法估计及其影响因素分析[J]. 地震地质,2019,41(1):21−43. WU Guo,ZHOU Qing,RAN Hongliu. The maximum likelihood estimation of b–value in magnitude–frequency relation and analysis of its influencing factors[J]. Seismology and Geology,2019,41(1):21−43.
[29] LIU Xiling,HAN Mengsi,HE Wei,et al. A new b value estimation method in rock acoustic emission testing[J]. Journal of Geophysical Research:Solid Earth,2020,125(12):e2020JB019658.
[30] 谷继成,魏富胜. 论地震活动性的定量化:地震活动度[J]. 中国地震,1987,3(增刊1):12−22. GU Jicheng,WEI Fusheng. The quantinigation of seismic activity:Seismicity[J]. Earthquake Research in China,1987,3(Sup.1):12−22.
[31] 王坤,马成功,敖锐,等. 基于XGBoost模型的阀门内漏信号特征选择方法[J]. 阀门,2024(10):1227−1234. WANG Kun,MA Chenggong,AO Rui,et al. Valve leakage signal feature selection method based on XGBoost model[J]. Valve Magazine,2024(10):1227−1234.
[32] SOWMYA R,PREMKUMAR M,JANGIR P. Newton–raphson–based optimizer:A new population–based metaheuristic algorithm for continuous optimization problems[J]. Engineering Applications of Artificial Intelligence,2024,128:107532. DOI: 10.1016/j.engappai.2023.107532
[33] 雷志勇,王家文,凡东,等. 基于1DCNN–BiLSTM–CBAM的煤巷顶板岩层地质特征随钻智能识别方法[J]. 煤田地质与勘探,2024,52(11):192−199. DOI: 10.12363/issn.1001-1986.24.06.0388 LEI Zhiyong,WANG Jiawen,FAN Dong,et al. An intelligent identifying–while–drilling method for geological features of roof strata in coal roadways based on a 1DCNN–BiLSTM–CBAM model[J]. Coal Geology & Exploration,2024,52(11):192−199. DOI: 10.12363/issn.1001-1986.24.06.0388
计量
- 文章访问数: 22
- HTML全文浏览量: 1
- PDF下载量: 4
