Inversion of electric field component Ex in the SOTEM method based on the improved particle swarm optimization algorithm
-
摘要:目的
针对电性源短偏移距瞬变电磁法(SOTEM)水平电场分量反演中传统算法易陷入局部极值的问题,提出一种融合重心反向学习策略的改进粒子群算法。
方法该算法通过引入重心反向学习策略,动态调整学习因子和自适应惯性权重,有效提升了全局搜索能力与收敛效率。研究构建了三层、五层及七层典型地电模型,来验证算法性能。
结果和结论研究结果表明:对于五层和七层地电模型,阻尼最小二乘算法的反演平均误差分别为0.34%和4.68%,改进粒子群算法反演平均误差分别为0.21%和0.87%,可见改进粒子群算法反演对复杂地电结构的识别精度提升显著。在多层数(≥5)及宽泛参数搜索区间条件下,三层和五层地电模型反演平均误差均小于 5%,验证了改进粒子群算法的有效性。利用某区实测数据进行阻尼最小二乘反演和改进粒子群算法反演,改进的粒子群算法较阻尼最小二乘算法有着较好的反演效果,反演结果与已知矿体的电性结构吻合较好,研究成果为提高SOTEM在矿产勘探中的分辨率提供了理论支持。
-
关键词:
- 电性源短偏移距瞬变电磁法 /
- 粒子群算法 /
- 反演 /
- 电场分量Ex
Abstract:ObjectiveThe inversion of the horizontal electric field component in the grounded-source short offset transient electromagnetic (SOTEM) method using traditional algorithms is prone to fall into local extrema. To address this challenge, this study proposed an improved particle swarm optimization (PSO) algorithm that integrates the center of gravity reverse learning strategy.
MethodsBased on the center of gravity reverse learning strategy, the improved PSO algorithm can dynamically adjust learning factors and the value of the adaptive inertia weight, thus improving the global search capability and convergence efficiency effectively. The performance of the improved PSO algorithm was verified using the typical three-, five-, and seven-layered geoelectric models constructed in this study.
Results and ConclusionsThe results of this study indicate that for the five- and seven-layered geoelectric models, the damped least squares method yielded average inversion errors of 0.34% and 4.68%, respectively, while the improved PSO algorithm yielded average inversion errors of 0.21% and 0.87%, respectively. This suggests that the improved PSO algorithm significantly improved the identification accuracy of complex geoelectric structures. Under the conditions of multi-layer (≥5) initial inversion intervals and wide search intervals, the improved PSO algorithm yielded average inversion errors of less than 5% for both three- and five-layered geoelectric models, substantiating its effectiveness. Inversion was conducted for the measured data from a certain mining area using the damped least squares method and the improved PSO algorithm. The inversion results demonstrate that the improved PSO algorithm outperformed the damped least squares method, with the inversion results of the improved PSO algorithm agreeing well with the electrical structure of the known ore body. The results of this study will provide theoretical support for improving the resolution of SOTEM in mineral exploration.
-
随着地球物理勘探技术的不断进步,电性源短偏移距瞬变电磁法(SOTEM)取得了显著发展。该方法通过接地长导线源向地下发射激励电流,在0.3~2.0倍探测深度的偏移距范围内观测纯二次电磁场信号,实现地下目标体的有效探测[1-3]。SOTEM以其野外施工灵活、探测深度大等优势,在金属矿探测和煤田地质调查等领域,表现出巨大的潜力[4-9]。电性源瞬变电磁法中,水平电场分量${E_x}$和垂直磁场分量${H_{\textit{z}}}$的衰减与平面分布特征与地下介质紧密相关,是SOTEM方法中的关键参数,特别是电场分量${E_x}$,对地下高阻和低阻目标具有较好的分辨率,可进一步在实际勘探中推广应用[10]。
电场分量Ex对地下的低阻体和高阻体都具有较强的敏感性,灵敏区域主要位于异常体的上方,与目标体位置对应[11]。具体而言,电场分量${E_x}$对低阻体的敏感区域位于赤道向区域,而对高阻体的敏感区域位于轴向区域[12]。与垂直磁场分量${H_{\textit{z}}}$相比,由于电场测量采用不极化电极接地,大地滤波作用使电场在电磁干扰情况下受影响远小于磁场。此外,水平电场分量${E_x}$对高阻层的分辨能力优于垂直磁场${H_{\textit{z}}}$,并且水平电场${E_x}$的探测精度随偏移距的增大而增大[13]。同时,在激电响应特性方面,水平电场${E_x}$受不同参数变化影响大于垂直磁场分量,这在实际应用中值得关注[14]。
瞬变电磁反演是一个复杂的非线性问题,传统线性反演方法在处理此类问题时,往往容易陷入局部最优解,且极大地依赖于初始模型的设定。因此,粒子群算法作为一种非线性反演方法,在电磁法数据处理领域受到了广泛关注。该算法借鉴了鸟群觅食的群体行为,通过个体间的信息共享与协作来探索问题的最优解。然而,经典的粒子群算法在应用于电磁法数据反演时,也有易陷入局部最优和搜索精度有限等难题。为此,众多学者对经典粒子群算法进行了多种改进,并成功将其应用于电磁法数据反演中,取得了实质性的进展[15-25],但该方法在电性源瞬变电磁电场反演中鲜有应用。
基于此,笔者提出一种基于改进粒子群算法的SOTEM水平电场分量${E_x}$一维反演方法。该方法利用粒子群算法的全局搜索能力和收敛速度快的优点,同时结合SOTEM水平电场分量${E_x}$的响应特性,以克服传统确定性反演方法易陷入局部极小的缺点,实现对地下目标体的反演,提高勘探分辨率,为拓展SOTEM在深部矿产勘探中的应用提供新的思路。
1 SOTEM水平电场分量一维正演
在求解电性源短偏移距瞬变电磁响应时,通常先计算出频率域响应,再通过频−时转换方法转换到时间域。首先将电性源视为由若干电偶极子源串联而成,其中单个电偶极子的水平电场分量${E_x}$在柱坐标下的频率域计算公式[26]如下:
$$ \begin{aligned} &E_r =\frac{I \mathrm{d} l}{2 \pi} \cos \varphi\left[\frac{\mathrm{i} \omega \mu}{r} \int_0^{\infty} \frac{1}{\lambda+u_1 / R^*} J_1(\lambda r) \mathrm{d} \lambda\right.- \\ &\qquad \left.\rho_1 \int_0^{\infty} \frac{\lambda u_1}{R} J_0(\lambda r) \mathrm{d} r+\frac{\rho_1}{r} \int_0^{\infty} \frac{u_1}{R} J_1(\lambda r) \mathrm{d} \lambda\right] \end{aligned} $$ (1) $$ \begin{aligned} & {E_\varphi } = \frac{{I{\text{d}}l}}{{2{\text{π }}}}\sin \varphi \left[ {\frac{{{\rho _1}}}{r}\int_0^\infty {\frac{{{u_1}}}{R}{J_1}\left( {\lambda r} \right){\text{d}}\lambda } } \right. -\\ &\qquad {{\text{i}}\omega \mu \int_0^\infty {\frac{\lambda }{{\lambda + {u_1}/{R^ * }}}} {J_0}\left( {\lambda r} \right){\text{d}}r}+ \\ &\qquad \left.\frac{{{\text{i}}\omega \mu }}{r}\int_0^\infty {\frac{1}{{\lambda + {u_1}/{R^ * }}}} {J_1}\left( {\lambda r} \right){\text{d}}\lambda\right] \end{aligned} $$ (2) 其中:
$$ \begin{aligned} &{R^*} = {\text{coth}}\left[ {u_1}{h_1} + {{\text{arcot}}{{\text{h}}}\frac{{{u_1}}}{{{u_2}}}} {\text{coth}}\Bigg( {u_2}{h_2} + \cdots +\right.\\ &\qquad \left. {{{\mathrm{arcoth}} }}\frac{{{u_{N - 1}}}}{{{u_N}}} \Bigg) \right]\end{aligned} $$ (3) $$ \begin{aligned} &R ={\text{coth}}\left[ {u_1}{h_1} + {\text{arcot}}{{\text{h}}}\frac{{{u_1}{\rho _1}}}{{{u_2}{\rho _2}}} {\text{coth}}\Bigg( {u_2}{h_2} + \cdots +\right. \\ &\qquad \left.{\text{arcot}}{{\text{h}}}\frac{{{u_{N - 1}}{\rho _{N - 1}}}}{{{u_N}{\rho _N}}} \Bigg) \right]\end{aligned} $$ (4) 其中,${u_j} = \sqrt {{\lambda ^2} - k_j^2} $,$k_j^2 = \dfrac{{{\text{i}}\omega \mu }}{{{\rho _j}}}$,$\coth x = $ $\dfrac{{\exp (x) + \exp ( - x)}}{{\exp (x) - \exp ( - x)}}$,$\lambda $为空间频率。当采用直角坐标时,由柱坐标和直角坐标之间的关系可得:
$$ {E_x} = {E_r}\cos \varphi - {E_\varphi }\sin \varphi $$ (5) 对于式(1)和式(2)中的贝塞尔积分,本文采用159点0阶和1阶汉克尔系数[27]进行求解,利用G-S变换进行频率域到时间域的转换[28]。
2 改进的粒子群反演算法
2.1 经典粒子群算法
粒子群智能算法(PSO)模拟了自然界中鸟群或鱼群等生物群体的觅食行为,通过粒子间的信息共享和协作来寻找最优解。在PSO中,每个粒子代表解空间中的一个候选解,其位置对应于优化问题的一个可能解,速度决定了粒子在解空间中的移动方向和距离。粒子通过追随个体历史最优解$ \left( {{S_\text{pbest}}} \right) $和群体历史最优解$ \left( {{S_\text{gbest}}} \right) $来更新自己的速度和位置,从而逐渐逼近全局最优解。标准粒子群算法公式如下:
$$ \begin{aligned} & v_{(i,d)}^{t + 1} = {\omega ^ * } \cdot v_{(i,d)}^t + {c_1} \cdot {\text{rand}}() \cdot \left( {{S_{{\text{pbest}}}}_{(i,d)}^t - x_{(i,d)}^t} \right) + \\ &\qquad {c_2} \cdot {\text{rand}}() \cdot \left( {{S_{{\text{gbest}}}}_{(i,d)}^t - x_{i(i,d)}^t} \right) \end{aligned} $$ (6) $$ x_{i,d}^{t + 1} = x_{i,d}^t + v_{i,d}^{t + 1} $$ (7) 在上述算法中,假设存在一个个体数量为N的种群,决策域为D维。每个粒子都有各自的位置和速度,对于第$i$个粒子,定义自己的位置:$ {x_i} = \left( {{x_{i,1}},{x_{i,2}}, \cdots {x_{i,d}}} \right) $和速度:${v_i} = \left( {{v_{i,1}},{v_{i,2}}, \cdots ,{v_{i,d}}} \right)$,个体最优位置$ {S_{{\text{pbest}}}}_{(i)} = \left( {{S_{{\text{pbest}}}}_{(i,1)},{S_{{\text{pbest}}}}_{(i,2)}, \cdots ,{S_{{\text{pbest}}}}_{(i,d)}} \right) $和群体最优位置$ {S}_{\text{gbest}}{}_{(i)}= \left({S}_{\text{gbest}}{}_{(i,\text{1})},{S}_{\text{gbest}}{}_{(i,\text{2})},\cdots ,{S}_{\text{gbest}}{}_{({i,}d)}\right) $ $(i = 1,2, \cdots n,d = 1, 2, \cdots, D)$。并根据式(6)和式(7)更新自身的速度和位置。${\omega ^ * }$是惯性权重,用来调整控制种群粒子在空间中搜索的飞行速度,较大的惯性权重值有利于粒子的全局搜索能力,避免值陷入极小,较小的惯性权重值有利于粒子的局部搜索能力,提高返回值的精度;rand()是(0,1)区间内的随机函数;${c_1}$,${c_2}$为学习因子,取值在区间[0,4],一般取$ {c_1} = {c_2} $,${c_1}$反映了粒子在局部的寻优能力,其值影响着反演的精度,${c_2}$体现着粒子的寻优能力,影响全局收敛的效果;$ t $为迭代次数。
2.2 优化粒子群算法
本文提出的优化粒子群算法是在传统粒子群算法的基础上,引入重心反向学习策略,避免粒子群算法在反演时陷入局部最优。同时也引入动态学习因子与自适应惯性权重[29],加速算法的收敛进程。
重心反向学习策略的主要思想是在粒子寻优的过程中,根据当前的解生成一个反向解,比较当前解与反向解的目标函数值,择优进入下一次迭代。传统的反向学习策略为利用边界值来计算反向点,但这种模式并没有完全利用整个种群的搜索信息。因此,S. Rahnamayan等 [30]提出基于重心的反向策略。具体方法为:设置${X_1},{X_2}, \cdot \cdot \cdot ,{X_n}$为D维空间的N个有质量的点,整体的重心为:
$$ M = \frac{{{X_1} + {X_2} + \cdots +{X_N}}}{N} $$ (8) 其种群中某一点的重心反向点则为${\bar X_i} = 2 M - {X_i}$。而重心反向点的位于一个具有动态边界的搜索空间,记为${x_{i,j}} \in \left[ {{a_j},{b_j}} \right]$。
$$ {a}_{j}=\mathrm{min}({x}_{i,j})\text{,}{b}_{j}=\mathrm{max}({x}_{i,j}) $$ (9) $$ {\bar x_{i,j}} = \left\{\begin{aligned} & {{a_j} + {\text{rand}}() \cdot \left( {{M_j} - {a_j}} \right)\quad {x_{i,j}} < {a_j}} \\ & {{M_j} + {\text{rand}}() \cdot \left( {{b_j} - {M_j}} \right)\quad {x_{i,j}} > {b_j}} \end{aligned} \right. $$ (10) 动态边界的计算方式如式(9),若其反向点超出边界,则按照式(10)重新计算其反向点。
在反演中,重心反向学习策略主要运用于对初始种群的反向策略以及在产生全局最优解$ {S_\text{gbest}} $时。对初始种群进行反向学习策略,可以选择位置更优的粒子生成新的优化初始种群。对最优解$ {S_\text{gbest}} $进行反向学习,与新生成的$ {S_\text{pbest}} $的适应值进行对比,选择最优值。
在传统的粒子群算法中,惯性权重值${\omega ^ * }$为恒定值,其值的大小影响着算法搜索的精度以及效率。为提高粒子群算法的搜索精度以及计算效率,本文对惯性权重值${\omega ^ * }$进行自适应调整,其表达式如下:
$$ \left\{\begin{aligned} & {\omega ^ * }{\text{ = }}{\omega _{\min }} + \frac{{\left( {{f_i} - {f_{\min }}} \right) \cdot \left( {{\omega _{\max }} - {\omega _{\min }}} \right)}}{{{f_{\mathrm{a}}} - {f_{\min }}}}\quad {f_i} \leqslant {f_a} \\ & {\omega ^ * }{\text{ = }}{\omega _{\max }}\qquad\qquad\qquad\qquad\qquad\quad\; {f_i} > {f_a} \end{aligned} \right. $$ (11) 在式(11)中,${\omega _{\max }}$和${\omega _{\min }}$为惯性权重${\omega ^ * }$的最大值和最小值,本文取0.9和0.4;${f_i}$为当前的最优粒子的适应度值;$ {f_{\mathrm{a}}} $为当前粒子种群的平均适应度值;$ {f_{\min}} $为当前粒子最小的适应度值。可以看出,惯性权重${\omega ^ * }$的调整是根据${f_i}$与$ {f_{\mathrm{a}}} $值的相对大小来调节,这将使粒子有着较大的搜索能力,提高获得最优粒子的效率。
与惯性权重值类似,当学习因子为一个恒定值时,影响粒子群在搜索过程中达到全局最优和局部最优的平衡。若粒子群在搜索初期更倾向于在全局最优解处收敛,便容易出现早熟现象,这个问题在多峰复杂函数上更为明显。因此为提高粒子的活性,提高粒子的个体搜索能力,本文采用下式提高搜索能力。
$$ \left\{ \begin{gathered} {c_1} = {c_{{\text{max}}}} - {c_{{\text{min}}}}\left( {t - 1} \right)/{t_{{\text{max}}}} \\ {c_2} = {c_{{\text{min}}}} + \left( {t - 1} \right)/{t_{{\text{max}}}} \\ \end{gathered} \right. $$ (12) 2.3 目标函数的建立
对于地下水平均匀的地电模型,其地电参数可用$ G $来表示,其中包括电阻率$\left( \rho \right)$和层厚$\left( h \right)$,具体表达式为:
$$ G=\left({\rho }_{1},{\rho }_{\text{2}},\cdots, {\rho }_{{n}},{h}_{1};{h}_{2},\cdots, {h}_{n}\right) $$ (13) 在进行粒子群反演时,根据地电模型参数建立一个基于适应度值的目标函数$\varPhi $,具体表示如下:
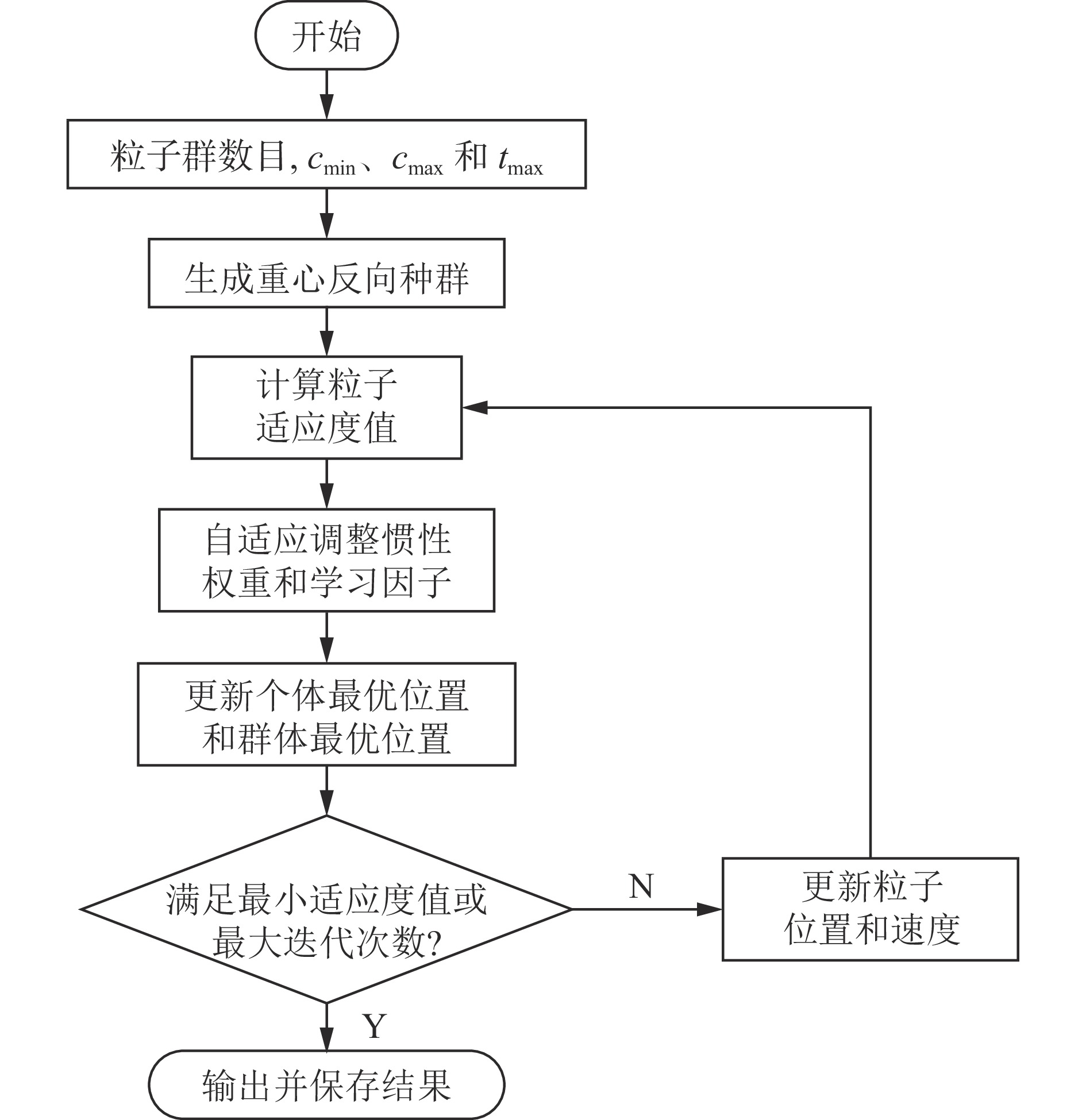
$$ \varPhi = {\left( {\frac{1}{n} \cdot \sum\nolimits_{k = 1}^n {{{\left( {\ln {{\hat y}_k} - \ln {y_k}\left( G \right)} \right)}^2}} } \right)^{1/n}} $$ (14) 根据上面的优化算法和目标函数的确立,改进粒子群算法的反演流程,如图1所示。
(1) 读取实测数据,将实际测量装置参数与正演参数保持一致。
(2) 设置粒子群的数目、每个维度粒子的取值范围、学习因子的最大值和最小值以及最大迭代次数等。
(3) 根据初始化种群生成重心反向种群,并计算2个粒子种群的适应度值,取得适应度值最优的粒子位置。
(4) 进行循环迭代,根据上次计算得到的适应度值,进行惯性权重值的调整,并根据迭代次数改变学习因子的值。更新粒子群的个体最优位置和群体最优位置。
(5) 计算当次迭代的适应度值是否满足设置的最小适应度值或是否达到最大迭代次数。若符合判断条件,输出计算结果;若不符合判断条件,再次更新粒子的位置和速度,重复迭代计算,直至符合判断条件。
3 理论模型反演
3.1 典型三层模型反演
首先,建立了4种典型的三层地电模型,分别为H模型、K模型、Q模型和A模型,具体参数如图2所示。正演参数设置为:发射电流为10 A,发射源长度为1 000 m;反演层数设置为3层,最大迭代次数为80,粒子种群数为40,${c_1} = 2$, ${c_2} = 1$;图2为改进的粒子群算法对4种典型地电模型的反演结果,其中为了有效验证改进后的粒子群算法在反演应用中的效果,将H模型和K模型设计3种偏移距进行反演,分别是100、500和1 000 m,Q模型和A模型的偏移距设置为500 m。由图2可知,改进粒子群反演算法对三层介质的地电模型有较理想的反演结果,并且在不同的偏移距同样有较好的反演结果,对模型的电阻率和深度都有较好的反映。
3.2 多层模型反演
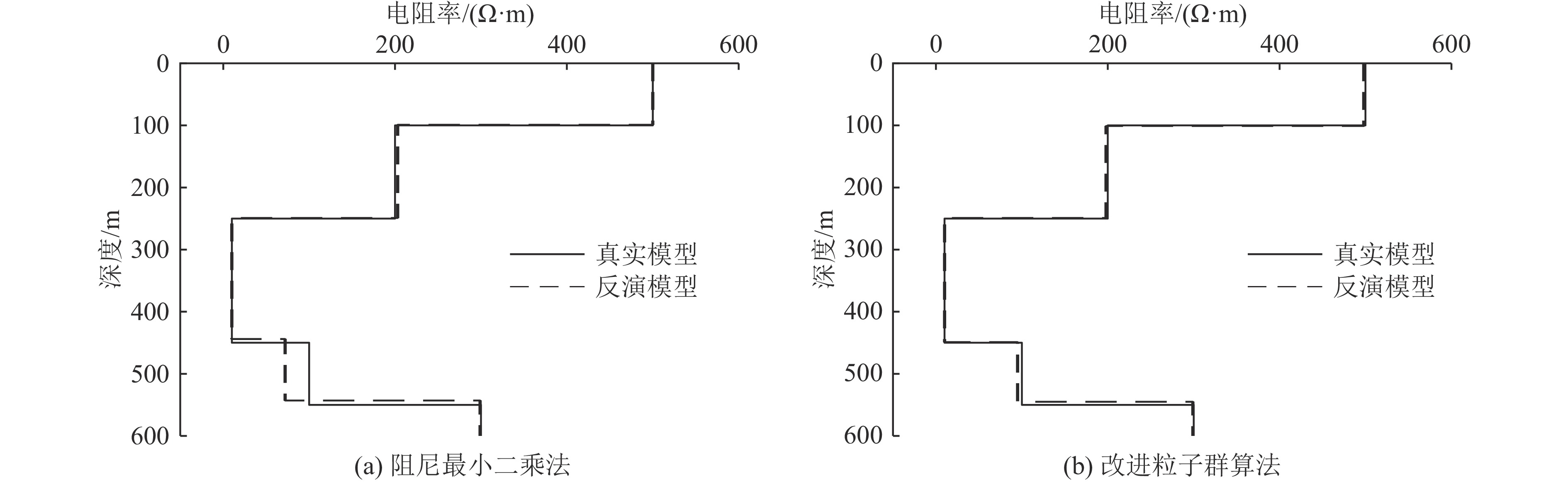
为进一步验证改进粒子群算法的反演效果,建立五层QHA地电模型和七层KHKHA型地电模型,将改进粒子群反演算法与阻尼最小二乘法反演进行对比,为更好地验证2种反演结果与真实模型的误差,反演模型参数与真实模型采用相同层数。由图3和图4可知,改进粒子群算法对五层和七层模型的反演效果要明显优于阻尼最小二乘法的反演结果,对多层模型的电阻率和深度都有较好的反映。阻尼最小二乘算法的反演平均误差分别为0.34%和4.68%改进粒子群算法的反演平均误差分别为0.21%和0.87%。真实模型参数见表1和表2。
表 1 五层QHA模型反演结果Table 1. Inversion results of five-layered QHA geoelectric models模型和算法 ρ1/(Ω·m) ρ2/(Ω·m) ρ3/(Ω·m) ρ4/(Ω·m) ρ5/(Ω·m) h1/m h4/m h3/m h4/m 真实模型 500 200 10 100 300 100 150 200 100 改进粒子群算法 498 198 10 95 299 101 148 200 96 阻尼最小二乘法 500 203 10 72 299 99 150 195 99 参数反演区间 [400,600] [150,250] [1,30] [50,150] [250,350] [50,150] [100,200] [150,250] [50,150] 表 2 七层KHKHA模型反演结果Table 2. Inversion results of seven-layered KHKHA geoelectric models模型和算法 ρ1/(Ω·m) ρ2/(Ω·m) ρ3/(Ω·m) ρ4/(Ω·m) ρ5/(Ω·m) ρ6/(Ω·m) ρ7/(Ω·m) h1/m h2/m h3/m h4/m h5/m h6/m 真实模型 100 500 10 200 50 100 500 100 50 100 50 100 100 改进粒子群算法 100 491 10 194 51 106 496 98 50 103 53 96 91 阻尼最小二乘法 109 600 11 150 67 88 419 88 67 121 82 94 90 反演参数区间 [50,150] [400,600] [1,30] [50,250] [10,100] [50,150] [400,600] [50,150] [10,100] [50,150] [10,100] [50,150] [50,150] 3.3 宽泛搜索空间粒子群反演
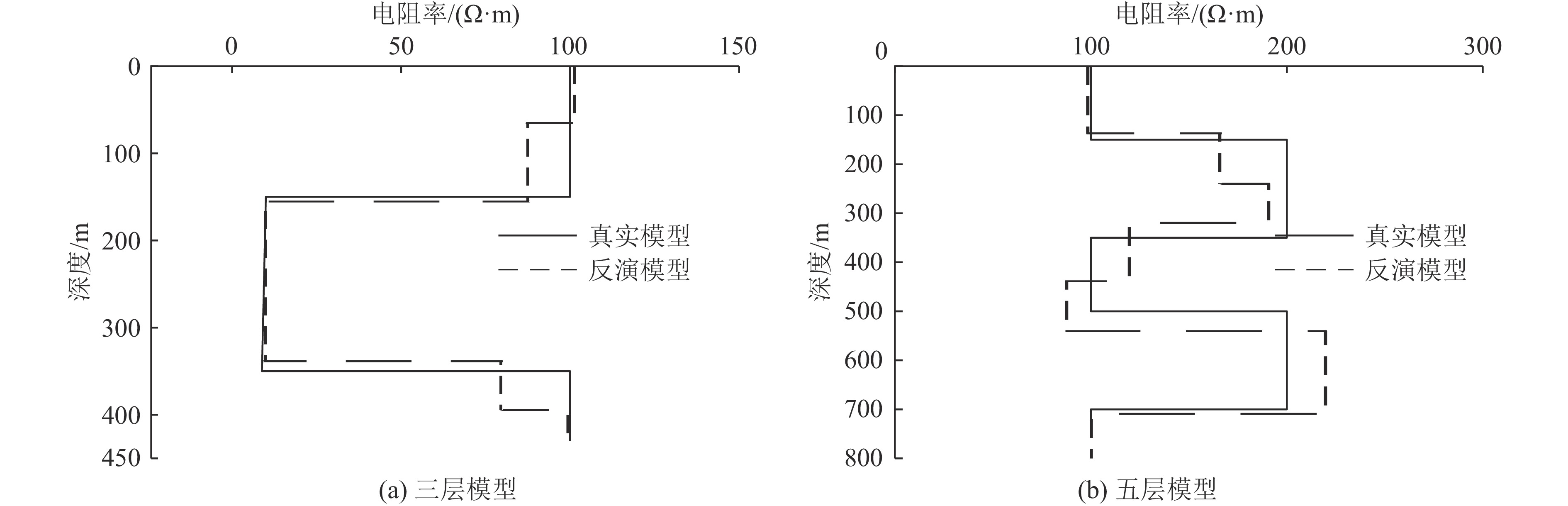
在实际勘探中,地下介质的电阻率和层厚往往难以准确预知,这增加了反演问题的复杂性。因此,对一个三层地电模型给定五层的初始反演区间,类似地将一个五层地电模型给定一个七层的初始反演区间,每层反演区间均使用宽泛搜索区间,验证改进粒子群算法的有效性。对于三层模型给定五层初始反演区间设置(表3),将五层模型给定七层反演区间(表4)。由图5可知,对于与初始模型层数不同的多层反演区间设置以及宽泛的搜索区间,改进的粒子群反演算法仍然可以较好地恢复地下的电性结构,并且三层和五层地电模型反演平均误差均小于5%。
表 3 三层模型反演Table 3. Inversion based on a three-layered model模型和反演区间 ρ1/(Ω·m) ρ2/(Ω·m) ρ3/(Ω·m) h1/m h2/m 真实模型 100 10 100 150 200 常规反演区间 [50,150] [5,30] [50,150] [100,200] [150,250] 三层反演区间 [5,350] [5,350] [5,350] [5,100] [5,100] 表 4 五层模型反演Table 4. Inversion based on a five-layered model模型和反演区间 ρ1/(Ω·m) ρ2/(Ω·m) ρ3/(Ω·m) ρ4/(Ω·m) ρ5/(Ω·m) h1/m h2/m h3/m h4/m 真实模型 100 200 100 200 100 150 200 150 200 常规反演区间 [50,150] [150,250] [50,150] [150,250] [50,150] [100,200] [150,250] [100,200] [150,250] 五层反演区间 [5,350] [5,350] [5,350] [5,350] [5,350] [5,150] [5,150] [5,150] [5,150] 4 应用实例
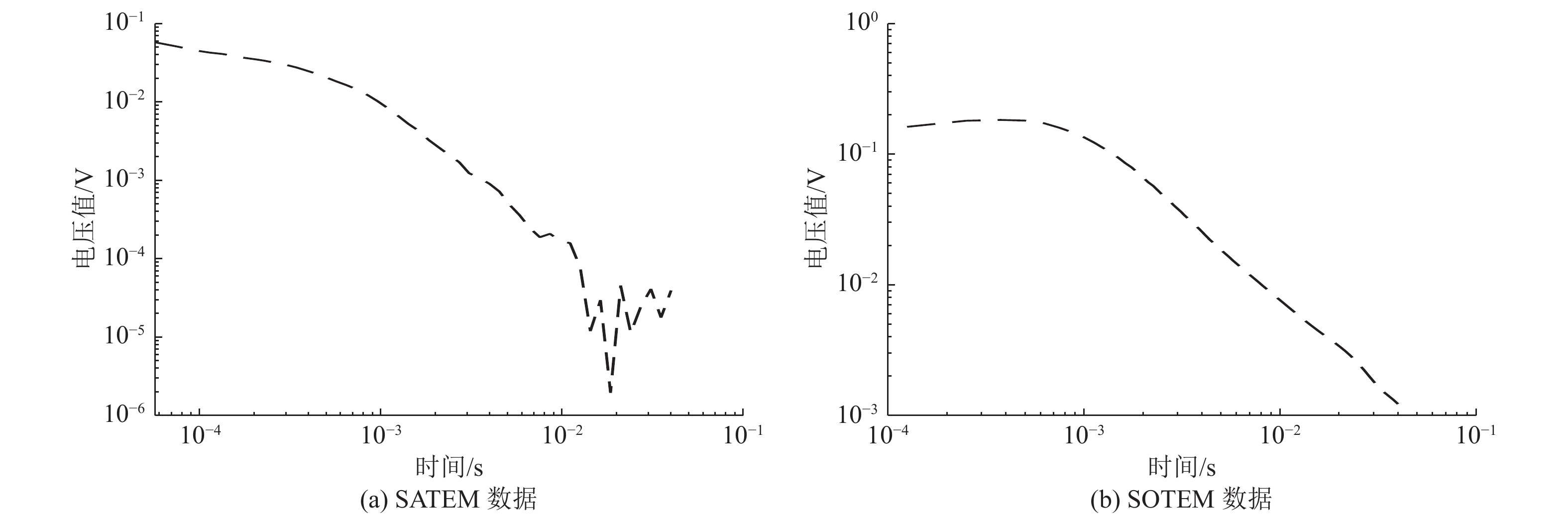
为验证该反演方法在水平电场反演时的适用性,本文选取了甘肃某矿区的SOTEM水平电场分量数据以及对应的电性源地空瞬变电磁(SATEM)数据进行处理,探测目标为低阻矿体。测区内包含多条SOTEM测线与地空瞬变电磁测线。本文选取其中一条穿过已知矿体的SOTEM测线进行反演,并与对应的SATEM测线对比分析。图6是选取的工区内某测点SOTEM和SATEM的衰减曲线。由图6a可见,该区域的干扰比较强,在地空瞬变电磁衰减曲线中,晚期的数据跳跃非常大,电磁干扰严重,这对于深部的探测的可信度造成了一定的影响。由图6b可知,电场衰减曲线基本光滑,在晚期的信号正常衰减,抗干扰能力较强,这也是采用电场分量${E_x}$的主要优势。
工区分布如图7所示,2种测量方式采用的发射电流为45 A,发射基频为5 Hz,发射源长度为2.59 km,走向为SW—NE,如图中红线所示。SOTEM测线和SATEM测线的走向与发射源相同,且起点均位于南侧。图中绿色线为SOTEM测线和SATEM测线,2条测线都分别有51个测点,点距均为20 m,2条测线总长度均为1 000 m,收发距离为400 m,观测时长50 ms, SATEM测线飞行高度为200 m,SOTEM测线和SATEM测线中后段均位于已知矿区。
利用改进的粒子群算法和阻尼最小二乘反演算法对SOTEM采集的水平电场分量数据进行反演。设置反演的初始种群数目为40,最大迭代拟合次数为80。将各点的反演结果进行组合,绘制为反演结果的电阻率−深度剖面,如图8a所示。 对SATEM测线数据进行视电阻率计算,绘制视电阻率−深度剖面图,如图8b所示。
由图8a可知,SOTEM测线范围内的地下电性结构总体表现为高阻−低阻−高阻的分布特征。SOTEM测线的0~600 m处为未知探测区域,600~1 000 m处属于已知矿体区域。根据反演结果图可见,在SOTEM测线的起始位置与测线200 m处深部存在明显低阻异常圈闭区域,深度大约在300 m;而在测线500 m处亦存在明显的低阻异常圈闭,其深度范围为800 m左右;在测线位置的800~1 000 m处可见低阻异常圈闭,其深度范围在800 m左右;该位置刚好位于已知矿区区域,具有明显的低阻异常圈闭,与SATEM测线深度−视电阻率断面图(图8b)相对比,SOTEM的反演结果分辨率高,能够较好地反映测区的地电结构;符合实际地层电性变化规律,从而验证了本文基于电场分量的优化粒子群算法反演的可靠性。
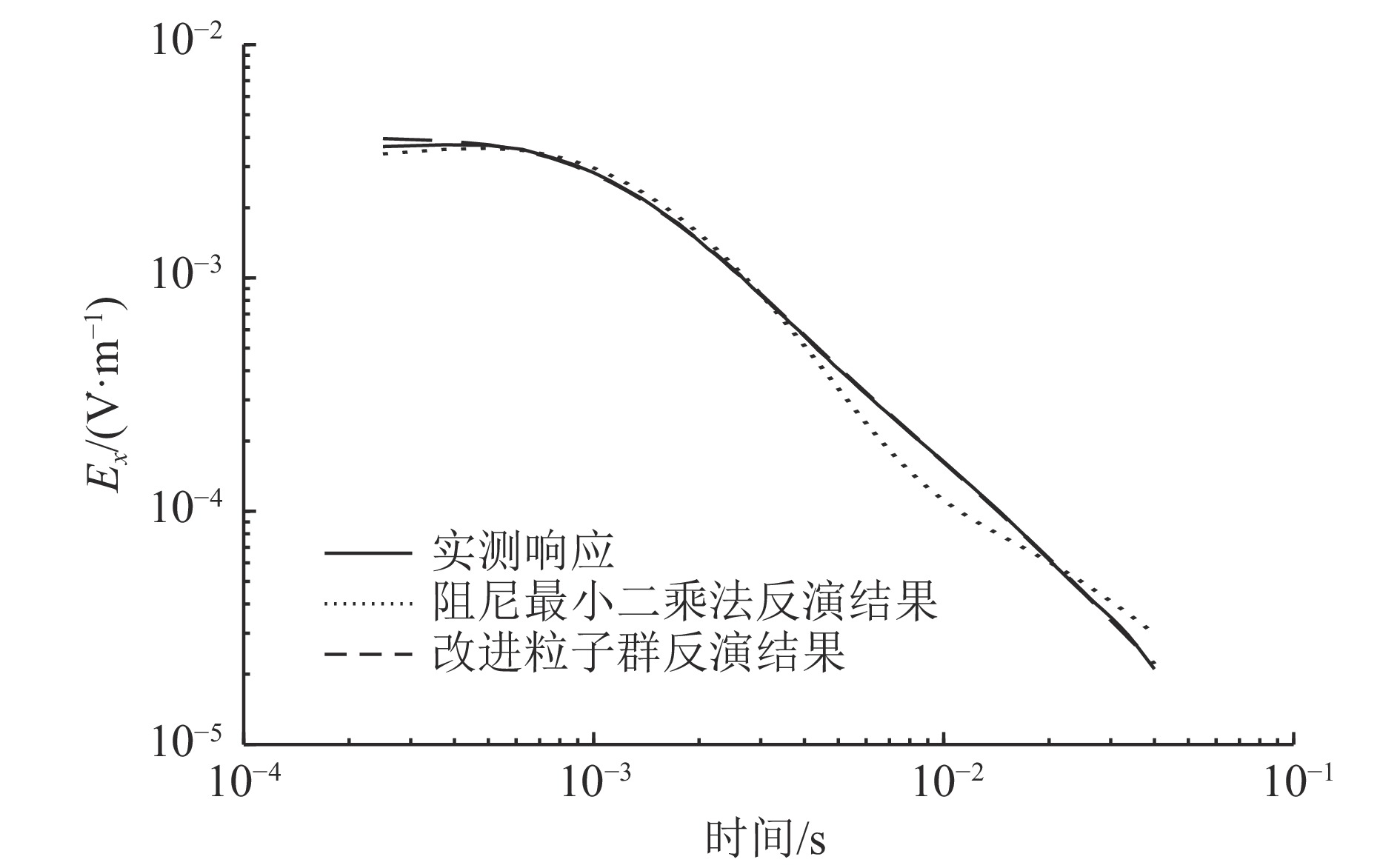
使用阻尼最小二乘算法对SOTEM测线进行反演得到反演断面图(图8c)。由图8c可知,改进粒子群算法的反演结果优于阻尼最小二乘算法。并将SOTEM测线其中一个测点进行反演,将得到的电阻率和层厚进行正演对比(图9),结果如图9所示,改进粒子群算法的反演模型的正演${E_x}$响应,与实测数据拟合较好,改进的粒子群反演算法优于阻尼最小二乘算法。
5 结 论
(1) 改进的粒子群反演算法通过引入重心反向学习策略、动态学习因子和自适应惯性权重,避免了反演结果陷入局部最优解的问题,并加速了反演的收敛过程。这一算法在处理非线性地球物理反演问题时,具有更高的精度和可靠性。
(2) 将改进粒子群反演算法应用于SOTEM水平电场分量${E_x}$的反演中,分别对3层、5层和7层理论地电模型进行反演,结果与真实模型具有较高的吻合度,这表明改进的粒子群算法对SOTEM水平电场分量${E_x}$反演具有较好的效果。
(3) 对某矿区的实测资料进行反演,发现反演结果与已知矿体的位置基本吻合,进一步验证了改进的粒子群算法在SOTEM电场分量反演中的可行性和实用性。
(4) 将改进的粒子群算法应用于SOTEM水平电场分量反演中,为在强干扰地区采用短偏移距瞬变电磁探测复杂地质电性结构提供了重要参考。将来需要进一步探索算法参数的优化方法,开展更多实际数据反演研究。
符号注释:
${a_j}$为粒子群搜索范围下限;${b_j}$为粒子群搜索范围上限;$ {c_{{\text{max}}}} $和$ {c_{{\text{min}}}} $分别为学习因子的上下限制;d为粒子i的维数;dl为单个电偶极子长度;$ {E_r} $为柱坐标系下$r$方向下响应;$ {E_\varphi } $为柱坐标系下$\varphi$方向下响应;$ {f_i} $为当前的最优粒子的适应度值;$ {f_a} $为当前粒子种群的平均适应度值;$ {f_{\min}} $为当前粒子最小的适应度值;$h$为地下介质层厚,m;${H_{\textit{z}}}$为垂直磁场分量;$i$为粒子在种群中的位置;I为发射电流强度,A;j为粒子所在的维度,j=1,2, $j = 1, 2, \cdots ,D$;${J_0}$和${J_1}$分别为0阶和1阶贝塞尔函数;$k_j^2$为电磁波传播波数的平方;$M$为D维空间有质量的点的重心;n为有质量的点的个数;$r$为测点到偶极中心矢径的模;$ {R^*} $和$ R $为核函数迭代计算式;$ t $为当前迭代次数;tmax为算法的最大迭代次数;${u_j}$ 为空间频率和电磁波传播波数的平方和再开方;$v$为粒子群中粒子速度;$ x $为粒子所在的位置;${\bar x_{i,j}}$为粒子所在重心反向点位置;${X_i}$为D维空间有质量的点;${\bar X_i}$为D维空间有质量的点的重心反向点;${y_k}$为正演响应值;${\hat y_k}$ 为观测响应值;$\lambda $称为空间频率;$\mu $为真空中的磁导率,H/m;ρ为电阻率,Ω·m;$ \varphi $为偶极中心矢径与x轴的夹角;$\omega $为角频率;${\omega _{\max }}$和${\omega _{\min }}$为惯性权重${\omega ^ * }$的最大值和最小值。
-
表 1 五层QHA模型反演结果
Table 1 Inversion results of five-layered QHA geoelectric models
模型和算法 ρ1/(Ω·m) ρ2/(Ω·m) ρ3/(Ω·m) ρ4/(Ω·m) ρ5/(Ω·m) h1/m h4/m h3/m h4/m 真实模型 500 200 10 100 300 100 150 200 100 改进粒子群算法 498 198 10 95 299 101 148 200 96 阻尼最小二乘法 500 203 10 72 299 99 150 195 99 参数反演区间 [400,600] [150,250] [1,30] [50,150] [250,350] [50,150] [100,200] [150,250] [50,150] 表 2 七层KHKHA模型反演结果
Table 2 Inversion results of seven-layered KHKHA geoelectric models
模型和算法 ρ1/(Ω·m) ρ2/(Ω·m) ρ3/(Ω·m) ρ4/(Ω·m) ρ5/(Ω·m) ρ6/(Ω·m) ρ7/(Ω·m) h1/m h2/m h3/m h4/m h5/m h6/m 真实模型 100 500 10 200 50 100 500 100 50 100 50 100 100 改进粒子群算法 100 491 10 194 51 106 496 98 50 103 53 96 91 阻尼最小二乘法 109 600 11 150 67 88 419 88 67 121 82 94 90 反演参数区间 [50,150] [400,600] [1,30] [50,250] [10,100] [50,150] [400,600] [50,150] [10,100] [50,150] [10,100] [50,150] [50,150] 表 3 三层模型反演
Table 3 Inversion based on a three-layered model
模型和反演区间 ρ1/(Ω·m) ρ2/(Ω·m) ρ3/(Ω·m) h1/m h2/m 真实模型 100 10 100 150 200 常规反演区间 [50,150] [5,30] [50,150] [100,200] [150,250] 三层反演区间 [5,350] [5,350] [5,350] [5,100] [5,100] 表 4 五层模型反演
Table 4 Inversion based on a five-layered model
模型和反演区间 ρ1/(Ω·m) ρ2/(Ω·m) ρ3/(Ω·m) ρ4/(Ω·m) ρ5/(Ω·m) h1/m h2/m h3/m h4/m 真实模型 100 200 100 200 100 150 200 150 200 常规反演区间 [50,150] [150,250] [50,150] [150,250] [50,150] [100,200] [150,250] [100,200] [150,250] 五层反演区间 [5,350] [5,350] [5,350] [5,350] [5,350] [5,150] [5,150] [5,150] [5,150] -
[1] 薛国强,陈卫营,周楠楠,等. 接地源瞬变电磁短偏移深部探测技术[J]. 地球物理学报,2013,56(1):255−261. DOI: 10.6038/cjg20130126 XUE Guoqiang,CHEN Weiying,ZHOU Nannan,et al. Short–offset TEM technique with a grounded wire source for deep sounding[J]. Chinese Journal of Geophysics,2013,56(1):255−261. DOI: 10.6038/cjg20130126
[2] 薛国强,闫述,陈卫营. 接地源短偏移瞬变电磁法研究展望[J]. 地球物理学进展,2014,29(1):177−181. DOI: 10.6038/pg20140124 XUE Guoqiang,YAN Shu,CHEN Weiying. Research prospect to grounded–wire TEM with short–offset[J]. Progress in Geophysics,2014,29(1):177−181. DOI: 10.6038/pg20140124
[3] 陈卫营,薛国强. 电性源瞬变电磁对薄层的探测能力[J]. 物探与化探,2015,39(4):775−779. CHEN Weiying,XUE Guoqiang. Detection capability of grounded electric source TEM for thin layer[J]. Geophysical and Geochemical Exploration,2015,39(4):775−779.
[4] 薛国强,陈卫营,武欣,等. 电性源短偏移距瞬变电磁研究进展[J]. 中国矿业大学学报,2020,49(2):215−226. XUE Guoqiang,CHEN Weiying,WU Xin,et al. Review on research of short–offset transient electromagnetic method[J]. Journal of China University of Mining & Technology,2020,49(2):215−226.
[5] 张继锋,孙乃泉,刘最亮,等. 电磁法在煤矿水害隐患探测方面的综述[J]. 煤田地质与勘探,2023,51(2):301−316. DOI: 10.12363/issn.1001-1986.22.12.0962 ZHANG Jifeng,SUN Naiquan,LIU Zuiliang,et al. Electromagnetic methods in the detection of water hazards in coal mines:A review[J]. Coal Geology & Exploration,2023,51(2):301−316. DOI: 10.12363/issn.1001-1986.22.12.0962
[6] XUE Guoqiang,WU Xin,CHEN Weiying,et al. Grounded–source short offset transient electromagnetic method:Theory and applications in deep mineral exploration[J]. Science China Earth Sciences,2025,68(2):626−638. DOI: 10.1007/s11430-024-1467-9
[7] 黄仕茂,杨光,王军成,等. SOTEM在厚覆盖煤矿采空区探测中的应用实例[J]. 物探与化探,2024,48(5):1208−1214. HUANG Shimao,YANG Guang,WANG Juncheng,et al. Application cases of the short–offset transient electromagnetic method in detecting goafs with thick overburden in a coal mine[J]. Geophysical and Geochemical Exploration,2024,48(5):1208−1214.
[8] 陈卫营,薛国强,赵平,等. 西藏羊八井地热田SOTEM探测及热储结构分析[J]. 地球物理学报,2023,66(11):4805−4816. DOI: 10.6038/cjg2023Q0848 CHEN Weiying,XUE Guoqiang,ZHAO Ping,et al. SOTEM exploration and reservoir structure analysis of Yangbajain geothermal field,Xizang[J]. Chinese Journal of Geophysics,2023,66(11):4805−4816. DOI: 10.6038/cjg2023Q0848
[9] 陈大磊,陈卫营,郭朋,等. SOTEM法在城镇强干扰环境下的应用:以坊子煤矿采空区为例[J]. 物探与化探,2020,44(5):1226−1232. CHEN Dalei,CHEN Weiying,GUO Peng,et al. The application of SOTEM method to populated areas:A case study of Fangzi coal mine goaf[J]. Geophysical and Geochemical Exploration,2020,44(5):1226−1232.
[10] HOU Dongyang,XUE Guoqiang,ZHOU Nannan,et al. Exploration of deep magnetite deposit under thick and conductive overburden with ex component of SOTEM:A case study in China[J]. Pure and Applied Geophysics,2019,176(2):857−871. DOI: 10.1007/s00024-018-2005-8
[11] 常江浩,薛国强. 电性源短偏移距瞬变电磁场扩散规律三维数值模拟[J]. 地球科学与环境学报,2020,42(6):711−721. CHANG Jianghao,XUE Guoqiang. Three–dimensional numerical simulation of diffusion law of short–offset grounded–wire transient electromagnetic field[J]. Journal of Earth Sciences and Environment,2020,42(6):711−721.
[12] 陈卫营,薛国强,崔江伟,等. SOTEM响应特性分析与最佳观测区域研究[J]. 地球物理学报,2016,59(2):739−748. DOI: 10.6038/cjg20160231 CHEN Weiying,XUE Guoqiang,CUI Jiangwei,et al. Study on the response and optimal observation area for SOTEM[J]. Chinese Journal of Geophysics,2016,59(2):739−748. DOI: 10.6038/cjg20160231
[13] 崔江伟,王施智,古瑶. 电性源瞬变电磁法E X分量和H Z分量对比分析[J]. 物探化探计算技术,2019,41(5):623−630. DOI: 10.3969/j.issn.1001-1749.2019.05.10 CUI Jiangwei,WANG Shizhi,GU Yao. Comparative analysis of E X component and H Z component of electrical source transient electromagnetic method[J]. Computing Techniques for Geophysical and Geochemical Exploration,2019,41(5):623−630. DOI: 10.3969/j.issn.1001-1749.2019.05.10
[14] 陈稳,薛国强,陈卫营,等. SOTEM多分量激电响应特性分析[J]. 地球物理学进展,2019,34(5):1859−1865. DOI: 10.6038/pg2019CC0257 CHEN Wen,XUE Guoqiang,CHEN Weiying,et al. Multi–component response of SOTEM with IP effect[J]. Progress in Geophysics,2019,34(5):1859−1865. DOI: 10.6038/pg2019CC0257
[15] RANJIT S,SHALIVAHAN S. Particle swarm optimization:A new tool to invert geophysical data[J]. Geophysics,2007,72(2):F75−F83. DOI: 10.1190/1.2432481
[16] 师学明,肖敏,范建柯,等. 大地电磁阻尼粒子群优化反演法研究[J]. 地球物理学报,2009,52(4):1114−1120. DOI: 10.3969/j.issn.0001-5733.2009.04.029 SHI Xueming,XIAO Min,FAN Jianke,et al. The damped PSO algorithm and its application for magnetotelluric sounding data inversion[J]. Chinese Journal of Geophysics,2009,52(4):1114−1120. DOI: 10.3969/j.issn.0001-5733.2009.04.029
[17] 李明星,肖林通,张倚瑞,等. 瞬变电磁粒子群优化反演研究[J]. 煤炭技术,2014,33(9):302−304. LI Mingxing,XIAO Lintong,ZHANG Yirui,et al. Research on particle swarm optimization inversion of transient electromagnetic method[J]. Coal Technology,2014,33(9):302−304.
[18] 何一鸣,薛国强,赵炀. 基于量子行为粒子群算法的航空瞬变电磁拟二维反演技术[J]. 地球科学与环境学报,2020,42(6):722−730. HE Yiming,XUE Guoqiang,ZHAO Yang. Quasi–2D stochastic inversion of airbone transient eletromagnetic data based on quantum–behaved particle swarm optimization algorithm[J]. Journal of Earth Sciences and Environment,2020,42(6):722−730.
[19] 王书明,底青云,夏彤,等. 瞬变电磁数据L–PSO反演方法[J]. 地球物理学报,2022,65(4):1482−1493. DOI: 10.6038/cjg2022P0264 WANG Shuming,DI Qingyun,XIA Tong,et al. Transient electromagnetic method inversion based on Lévy flight–particle swarm optimization[J]. Chinese Journal of Geophysics,2022,65(4):1482−1493. DOI: 10.6038/cjg2022P0264
[20] 董毅,仝景阳,吴佩凝,等. 薄煤层采空区等值反磁通瞬变电磁GAPSO反演研究[J]. 工程地球物理学报,2025,22(1):50−55. DOI: 10.3969/j.issn.1672-7940.2025.01.006 DONG Yi,TONG Jingyang,WU Peining,et al. Research on GAPSO inversion of the opposing coils transient electromagnetic method for goaf detection in thin coal seams[J]. Chinese Journal of Engineering Geophysics,2025,22(1):50−55. DOI: 10.3969/j.issn.1672-7940.2025.01.006
[21] 卫伟,赵弘. 基于粒子群算法的瞬变电磁检测小车结构优化[J]. 石油机械,2024,52(3):117−125. WEI Wei,ZHAO Hong. Structural optimization of transient electromagnetic detection cart based on particle swarm algorithm[J]. China Petroleum Machinery,2024,52(3):117−125.
[22] 余建国,田宝,周鹏,等. 基于CPSO–ICA的航空瞬变电磁信号去噪方法研究[J]. 信阳师范学院学报(自然科学版),2023,36(4):611−617. YU Jianguo,TIAN Bao,ZHOU Peng,et al. Research on method of airborne transient electromagnetic signal denoising based on CPSO–ICA[J]. Journal of Xinyang Normal University (Natural Science Edition),2023,36(4):611−617.
[23] 徐正玉,付能翼,周洁,等. 瞬变电磁法非线性优化反演算法对比[J]. 吉林大学学报(地球科学版),2022,52(3):744−753. XU Zhengyu,FU Nengyi,ZHOU Jie,et al. Comparison of nonlinear optimization inversion algorithms of transient electromagnetic method[J]. Journal of Jilin University (Earth Science Edition),2022,52(3):744−753.
[24] 黄炜伟. 基于粒子群的全空间瞬变电磁二维反演方法研究[J]. 工矿自动化,2021,47(4):79−84. HUANG Weiwei. Research on two–dimensional inversion method of transient electromagnetic in whole–space based on particle swarm[J]. Industry and Mine Automation,2021,47(4):79−84.
[25] 黄刚,杨海燕,余国锋,等. 圆锥型场源瞬变电磁数据AWPSO算法优化反演[J]. 地球物理学进展,2021,36(4):1521−1530. DOI: 10.6038/pg2021EE0315 HUANG Gang,YANG Haiyan,YU Guofeng,et al. Optimal inversion of transient electromagnetic data with a conical source excitation based on AWPSO algorithm[J]. Progress in Geophysics,2021,36(4):1521−1530. DOI: 10.6038/pg2021EE0315
[26] KAUFMAN A A,KELLER G V. Frequency and transient soundings[M]. Amsterdam:Elsevier,1983.
[27] 蔡盛. 快速汉克尔变换及其在正演计算中的应用[J]. 地球物理学进展,2014,29(3):1384−1390. DOI: 10.6038/pg20140353 CAI Sheng. The fast Hankel transformation and its applications in forward calculations[J]. Progress in Geophysics,2014,29(3):1384−1390. DOI: 10.6038/pg20140353
[28] 朴化荣,殷长春. 利用G–S逆拉氏变换法计算瞬变测深正演问题[J]. 物化探计算技术,1987,9(4):295−302. PIAO Huarong,YIN Changchun. Calculation of transient E. M. sounding using the Gaver–Stehfest inverse Laplace transform method[J]. Computing Techniques for Geophysical and Geochemical Exploration,1987,9(4):295−302.
[29] 董丽凤,陈阳,巫光福. 动态学习混沌映射的粒子群算法[J]. 计算机应用研究,2019,36(5):1319−1322. DONG Lifeng,CHEN Yang,WU Guangfu. Chaotic mapping particle swarm optimization algorithm based on variable learning factors[J]. Application Research of Computers,2019,36(5):1319−1322.
[30] RAHNAMAYAN S,JESUTHASAN J,BOURENNANI F,et al. Computing opposition by involving entire population[C]//2014 IEEE Congress on Evolutionary Computation (CEC). Beijing:IEEE,2014:1800–1807.







 下载:
下载: