A method for high-accuracy localization of microseismic sources in mines based on finite element simulation
-
摘要:目的和方法
矿井微震监测技术通过捕捉岩层内部结构在受力变形及破坏过程中产生的低频振动信号，来反映岩层变形及破坏情况，从而实现突水预警和地质灾害预测。其中，声源定位技术是关键环节，能够确定能量释放位置，预警潜在的灾害。目前，时差法用于声源定位存在算法复杂、定位精度受探头布置影响显著，以及对复杂地层结构适应性较差等问题。针对不同地层结构，基于有限元法，模拟弹性波在地层中的传播，考虑不同地层界面的透射、反射和衍射效应，研究了不同反演模型及探头布置方式对定位精度的影响。
结果和结论研究结果表明：点声源控制模型能较好地模拟弹性波在岩石中的传播，而正交探头布置方式在声源定位中表现更佳。在平面均质材料中，相较于双三角探头簇，单正方形探头簇定位误差降低了0.6%，双正方形探头簇提高了1.69%的精度；在平面层状结构中，双三角形探头簇采用透射反演法相比均速反演法精度提升15%，双正方形探头簇则提升了14.9%；在三维层状结构中，直角四面体探头簇的透射反演法精度提高了14.5%。总体而言，反演模型对定位精度的影响更为显著，提出的数值模拟方法能够通过时差法透射反演实现高精度、快速的声源定位。研究结果为矿井微震与微震监测预警系统的优化提供了重要参考。
Abstract:Objective and MethodsMicroseismic monitoring technology for mines can reflect the deformations and failure of rock layers by capturing low-frequency vibration signals their internal structure generated during the stress-induced deformation and failure of them. Accordingly, water inrush warnings and geologic hazard prediction can be achieved. Acoustic source localization, allowing for the localization of energy release and the early warning of potential hazards, plays a key role in this technology. Presently, when used for acoustic source localization, the time difference of arrival (TDOA) method is facing issues including high algorithmic complexity, significant impacts of probe arrangement on the localization accuracy, and low adaptability to complex stratigraphic structures. Using the finite element method, this study simulated the elastic wave propagation in various stratigraphic structures. Considering the transmission, reflection, and diffraction effects at various stratigraphic boundaries, this study investigated the impacts of various inversion models and probe arrangements on the localization accuracy.
Results and ConclusionsThe results indicate that the point source control models can effectively simulate the elastic wave propagation in rocks, with the orthogonal probe arrangement delivering superior performance in the acoustic source localization. In planar homogeneous materials, compared to the probe sets arranged in double triangles, the probe sets arranged in a single square exhibited a decrease of 0.6% in the localization error, while probe sets arranged in double squares displayed an increase of 1.69% in the localization accuracy. In a planar layered structure, compared to uniform velocity inversion, the transmission inversion increased the localization accuracy by 15% in the case of probe sets with a double triangle arrangement and by 14.9% for a probe set with a double square arrangement. In a three-dimensional layered structure, compared to uniform velocity inversion, the transmission inversion increased the localization accuracy by 14.5% in the case of the probe set arranged in a trirectangular tetrahedron. Overall, the inversion method produces more significant impacts on the localization accuracy than the probe arrangement, and the proposed numerical method enables high-accuracy, rapid acoustic source localization using the TDOA method and transmission inversion. The results of this study provide a valuable reference for optimizing microseismic monitoring and early warning systems for mines.
-
矿井水害是矿井建设与生产中的重大隐患，国内外科研工作者在矿井水害防治方面持续进行了大量研究和实践[1-6]。矿井声发射监测技术作为一种先进的无损检测手段，通过捕捉岩层内部结构在受力变形及破坏过程中产生的低频振动信号，反映矿井生产中岩层结构的稳定性，矿井中的低频声发射可以称为微震活动，因为它们的机制和在岩体破坏监测中的应用非常相似[7-9]。声源定位技术是矿井声发射及微震监测预警系统的核心，能够监测并确定矿井内部微小能量释放的位置，在矿井安全监控，特别是煤矿突水预警和岩爆预测等领域具有重要应用价值[10-24]。
时差定位法是微震源定位监测中应用最广泛的方法，具体包括USBM微震源定位法[25]、Geiger法[26]、Powell法[27]、粒子群算法[28]和单纯形定位算法[29]等。其中，Geiger定位方法作为时差定位法中的经典方法，得到了广泛应用和改进。例如，黄晓红等[30]提出结合全相位原理与Geiger定位的方法，以提升岩石微震源定位的精确度并减少迭代次数；林峰等[31]将线性定位方法与Geiger法相结合，避免了初始值选择不当导致的定位精度偏低问题；赵勇胜等[32]将角度法与时差法结合，开发出一种探头定位声发射源的新方法；Yu Huagang等[33]利用到达时间差(TDOA)和频率差(FDOA)的测量值，提出了一种约束最小二乘(CLS)算法，用于估计移动声源的位置和速度；李楠等[34]采用L1范数统计方法对声发射源定位进行残差分析，提出了声发射源定位的误差空间概念。
尽管时差定位方法具有较高的定位精度，但其算法复杂且对探头布置的空间要求较高，限制了其在工程应用中的快速计算。因此，亟需开发一种在探头布置和计算方法上均适用于矿井微震反演定位的技术。
针对现有方法在微震反演定位方面的不足，本文采用有限元方法，通过Comsol软件模拟弹性波的传播过程，以监测微小位移的方式，进行仿真研究。研究重点包括分析2种不同探头分布结构在处理平面问题上的优劣，并优化经验均匀波速算法在层状结构中的反演精度。通过有限元仿真，旨在提升微震源定位的准确性和计算效率，为矿井微震和微震监测预警系统的优化提供理论支持和技术依据。
1 时差反演定位法定义及探头簇组合形式
时差反演定位法基于来自同一微震源的信号在到达不同布置位置的探头时所产生的时间差。该方法结合探头的空间布置信息，构建与微震源位置相关的数学模型，进而精确反演出微震源与各探头之间的相对空间位置。随着微震监测技术的进步和设备状态监测要求的提升，时差定位方法凭借其高定位精度已成为广泛使用的微震源定位技术之一[35]。
在处理二维平面问题时，通常采用等腰直角三角形探头簇和正方形探头簇来限制正交探头的平面分布[36]。而在三维空间问题的处理中，则采用两组直角四面体探头簇来限制正交探头在三维空间的分布[37]。
1.1 等腰直角三角形探头分布反演定位法
如图1所示，在平面坐标系中布置3个探头，构成等腰直角三角形探头簇。3个探头的坐标Ri分别为(xi,yi)，其中i=1,2,3。已知各探头间的坐标关系，设点声源的坐标为(xS，yS)。由于探头之间的距离远小于微震源到探头的距离，在反演计算时可以忽略探头间距的影响。不同探头接收到的首波到达时间有所不同，且由于探头监测的是首波传播，后续波的反射和叠加效应可以忽略不计。
![]()
图 1 直角三角形探头簇微震源反演Figure 1. Inversion for a microseismic source based on two probe sets each arranged in an right triangle在探头R2位置处，声源的传播角度为θ，点声源和探头R2的关系可表示为：
$$ \theta = {\text{ta}}{{\text{n}}^{{{ - 1}}}}\left( {\frac{{{y_S} - {y_2}}}{{{x_S} - {x_2}}}} \right) $$ (1) 基于时差信息：
$$ \Delta {t_{12}} = {t_1} - {t_2} = \frac{{d\cos \theta }}{{{c_{\mathrm{p}}}}} $$ (2) 在已知探头间距d的情况下，点声源与探头R2之间的夹角θ仅与时差信息有关：
$$ \theta = {\tan ^{ - 1}}\left( {\frac{{\Delta {t_{32}}}}{{\Delta {t_{12}}}}} \right) $$ (3) 需要注意的是，通过一组等腰直角三角形探头簇可以确定一条方向已知的直线，若布置2组探头簇，则可以得到2条直线交于一点，理论上该交点即为点声源的位置。因此，该种方法需要至少2个三角形探头簇，共计6个探头。
1.2 正方形探头分布反演定位法
如图2所示，采用正方形探头布置。同理，每2个探头簇可以通过时差反演得到点声源所在的2条传播路径。结合探头布置的空间坐标和监测到的时间差，可以计算出点声源弹性波的传播方位角θ。仅通过一组正方形探头簇即可精确反演出声源的位置，双正方形探头则需要8个探头。双探头簇结构可显著提高定位精度。
![]()
图 2 正方形探头簇微震源反演Figure 2. Inversion for a microseismic source based on a probe set arranged in a square2 探头簇组合的定位效果数值模拟
分别以均匀各向同性地层、层状各向同性地层和层状各向异性地层为例，研究不同探头簇组合方式的定位效果，为声源定位提供依据。
2.1 平面均匀结构及点声源控制模型
在均匀各向同性材料中，反演过程只需考虑波速控制模型和探头的分布形式，因此，可以简化为二维模型。本文建立了如图3所示的二维模型，模型长度为200 m，高度为100 m，边界设定为10 m宽的低反射虚拟域，以减少边界反射对计算结果的影响。为模拟地层损伤产生的弹性波传播至监测探头的过程，模型中设置了8个探针点作为监测探头。假设地层材料为砂岩，首波为P波，其波速计算公式见下式，砂岩的密度及声波传播特性见表1。
表 1 均质平面结构波速模型物性参数Table 1. Physical parameters of the velocity model for a homogeneous planar structure材料属性 密度ρ/(kg·m−3) P波波速cP/(m·s−1) S波波速cS/(m·s−1) 砂岩 2520 3850 2082 声源信息通过面空间函数与时间函数提供，在平面法向上设置单位面积载荷作为初始激励，激励强度参考砂岩的抗拉损伤强度(约为4.6 MPa)，激励的中心频率设为100 Hz。由此产生的弹性波阵面呈圆形，可视为点声源[38]。
$$ c=\sqrt{\frac{E(1-\mu )}{\rho (1+\mu )(1-2\mu )}} $$ (4) 点声源的空间分布符合二元高斯分布函数，见下式。
$$ \text{Gspace}(x,y)=A{\left\{(\text{πd}S)\mathrm{exp}\left[\frac{-({(x-{x}_{0})}^{2}+{(y-{y}_{0})}^{2})}{\text{d}S}\right]\right\}}^{-1} $$ (5) 图4展示了点声源空间函数分布。其中(x,y)为点声源坐标，z为声源强度，单位为1，具体数值见色标。
点声源的时间分布由雷克子波给出，见下式。
$$ {\text{Gtime}}(t) = [1 - 2{{\text{π }}^2}f_0^2{(t - {t_0})^2}]{\text{exp}}[ - {{\text{π }}^2}f_0^2{(t - {t_0})^2}] $$ (6) f0为主频率，为100 Hz；t0为延迟时间，为0.06 s；激励时间函数和频谱如图5所示。
![]()
图 5 点声源激励时间函数及其频谱分布Figure 5. Time function of acoustic point source excitation and its frequency spectrum为了避免边界处弹性波反射对监测结果的影响，模型的4个方向均设置了宽度为10 m的“回”字形低反射虚拟域。同时，在点声源位置(x0,y0)处施加平面载荷，载荷的大小为时间函数与空间函数的乘积，表示为Gspace(x,y)×Gtime(t)，单位为Pa，并作为点声源的脉冲激励。有限元网格的剖分采用四边形映射，结合控制网格单元大小的方式进行。其中，最大网格单元的尺寸由已知材料的最小波速控制，具体公式为：
$$ {L_{{\text{max}}}} \leqslant \frac{{c{_{{\mathrm{S}}\min }}}}{{1.33{f_0}}} $$ (7) 2.2 平面均匀结构探头簇布置及微震源反演定位结果分析
2.2.1 点声源在均质结构中的传播
由于弹性波的传播依靠的是微小粒子之间的应变响应，为获取不同时刻点声源在均质结构中的传播情况，模型通过传播面的法向振动来表征弹性波的传播过程。
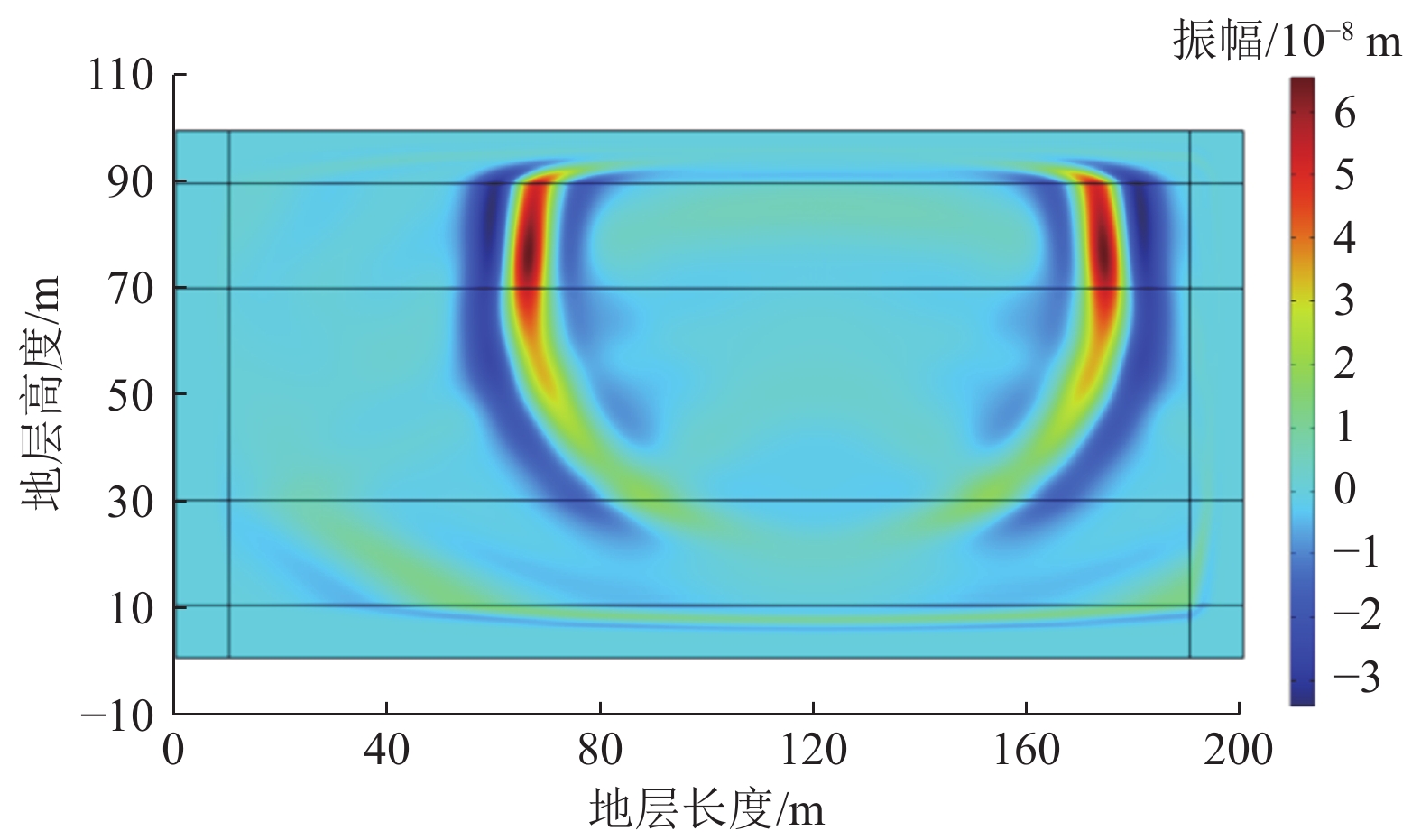
图6a展示了0.06 s时位于(120,80)点声源的弹性波波阵面。此时，由于点激励的作用，固定坐标处出现了明显的高亮点声源。随着时间的推移，弹性波以点声源为中心呈现圆形波阵面传播，传播形式为纵波和横波。到0.073 s时(图6b)，可以清晰看到纵波在前横波在后的传播顺序。由于模型的限制，位于上边界附近的弹性波率先被虚构域吸收层吸收。当点声源传播至0.119 s时(图6c)，最后一缕横波抵达虚构域吸收层，模型中的法向位移趋于0，标志着本次微震事件的结束。
![]()
图 6 不同时刻点声源位于(120,80)处弹性波阵面Figure 6. Elastic wave fronts of an acoustic point source at (120, 80) under varying times将探头布置在R1—R8位置，形成2个探头簇，用于接收并记录来自点声源的弹性波信息。图7展示了探头R1接收到的弹性波形图。由图7可知，探头接收到的弹性波与点声源初始激励(经过衰减的雷克子波)高度相似。波形清晰地显示出纵波与横波的分批到达情况。由于探头记录的是法向振动，横波的峰值幅度大于纵波峰值。
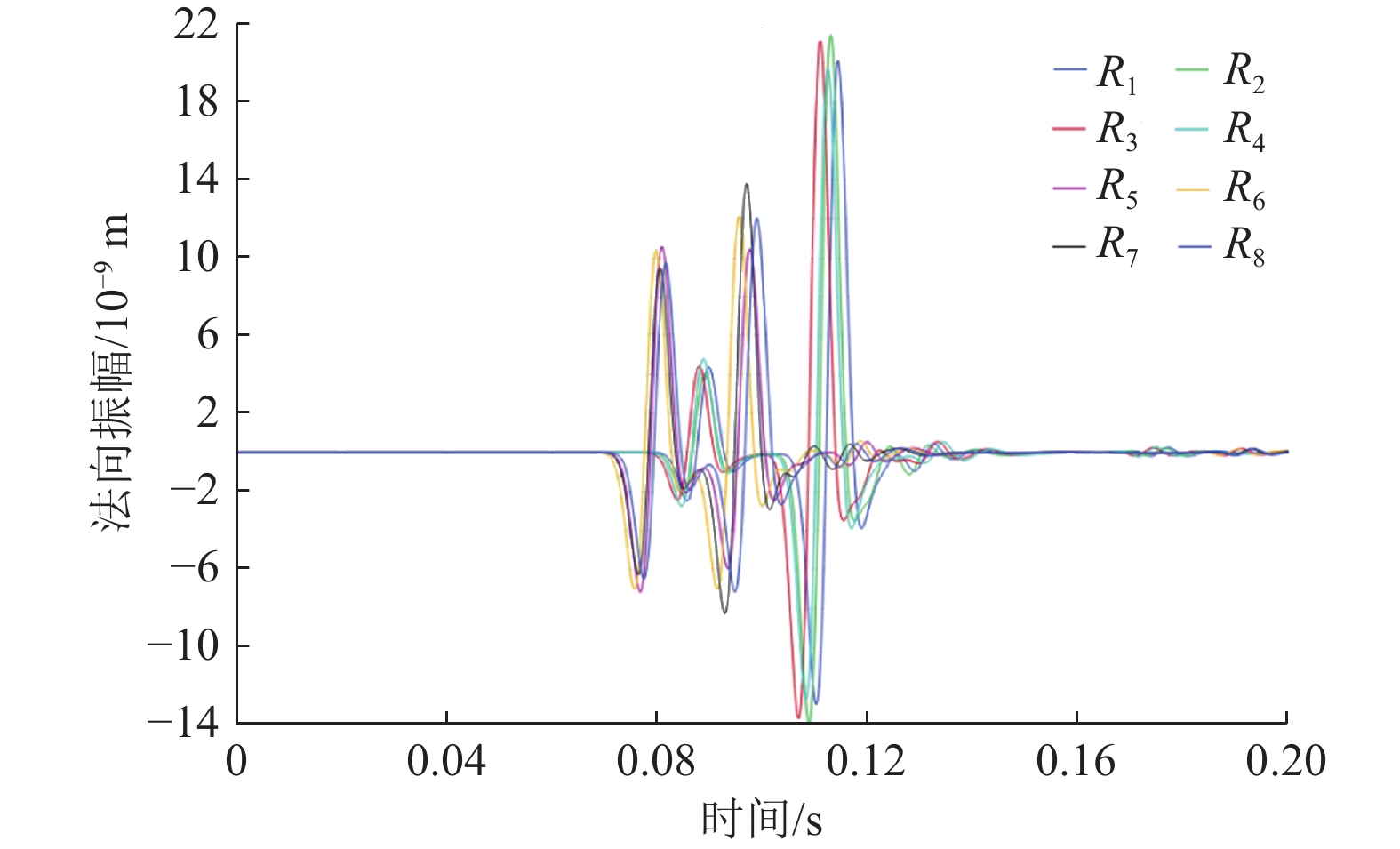
图8展示了8个探头接收到的弹性波形特征。通过分析首波(纵波)波峰的到达时间，计算出探头的时差信息，为后续的反演定位计算提供了重要依据。
2.2.2 多结构探头反演定位效果对比分析
在模型中布置了R1—R8共8个探头，形成了2个正方形探头簇，具体位置如图3所示，通过分别关闭探头R1和R8，构建出直角三角形探头簇。
从监测到的探头法向位移参数中读取首波到达时间，结果见表2。基于探头的坐标信息：$x_2=30，x_3= x_4=35 $，$y_2=y_3=30，y_4=15 $。
表 2 探头布置坐标及首波到时实际监测数据Table 2. Probe coordinates and actual monitoring data of first arrival times微震探头 R1 R2 R3 R4 R5 R6 R7 R8 坐标/(m,m) (30,15) (30,20) (35,20) (35,15) (160,15) (160,20) (165,20) (165,15) 首波时间/s 0.089 88 0.089 02 0.087 96 0.088 76 0.080 90 0.079 79 0.080 53 0.081 60 计算得出时差信息详见表3。
表 3 计算获得的各探头时差信息Table 3. Calculated differences in the arrival times at various probes时差 Δt12 Δt23 Δt34 Δt41 Δt56 Δt67 Δt78 Δt85 计算值/s 0.00086 0.00106 0.0008 0.00112 0.00111 0.00074 0.00179 0.0007 通过2个时差信息可以确定一条带有方向的反演路径，用以下公式计算2个探头簇的传播角度。
$$ \theta = \arctan \frac{{\Delta {t_{34}}}}{{\Delta {t_{23}}}} = 37.04 $$ (8) $$ \delta = \arctan \frac{{\Delta {t_{56}}}}{{\Delta {t_{67}}}} = 56.31 $$ (9) 据此可得声源的坐标为：xS=118.16，yS=82.76，与实际点声源坐标(120，80)吻合。定位结果如图9所示。
为了进一步验证该方法，改变点声源位置，进行多次仿真研究，通过探头接收的弹性波形图，读取所需的到达时差信息，进而反演点声源位置，并按下式计算定位误差$\Delta L $，仿真反演结果见表4。
表 4 平面均匀材料的双三角探头点声源反演定位结果Table 4. Locations of acoustic point sources in planar homogeneous materials derived through inversion based on probe sets arranged in double triangles点声源坐标/(m,m) 双三角探头簇
反演位置/(m,m)定位误差/m 相对误差/% (120,80) (118.16,82.76) 3.32 (1.53,3.45) (100,70) (98.52,71.81) 2.34 (1.48,2.59) (80,80) (81.02,78.84) 1.54 (1.28,1.45) (60,70) (61.37,71.21) 1.83 (2.28,1.73) (50,60) (51.56,58.97) 1.87 (3.12,1.72) $$ \Delta L=\sqrt{({x}_{{\mathrm{S}}}-{x}_{i}{)}^{2}+({y}_{{\mathrm{S}}}-{y}_{i}{)}^{2}} $$ (10) 由定位结果可知，双三角形探头簇定位的误差整体控制在3.4 m以下，相对误差整体低于3.5%。
将图3所示探头R1—R4开启，关闭R5—R8，形成一个正方形探头簇。根据表2中的探头坐标和点声源到达时间信息，每2个探头可求出一个点声源坐标，最多可获得6个定位点。以其中2个角度进行反演计算，得出点声源坐标为：xS=115.12，yS=77.23，与实际点声源坐标(120，80)存在较大误差。为了提升定位精度，可启用探头R5—R8，形成双正方形探头簇，分别使用两侧正方形探头簇定位，反演路径如图10所示。结果表明，若要进一步提高定位精度，需要同时使用两侧探头簇。
![]()
图 10 双正方形探头反演结果Figure 10. Inversion results based on double probe sets each arranged in a square通过改变点声源位置，进行多次数值模拟，利用探头接收到的弹性波形图求得所需的到达时差信息，并预测声源位置，计算定位误差，仿真结果见表5。
表 5 平面均质材料的正方形探头点声源反演定位结果Table 5. Locations of acoustic point sources in planar homogeneous materials derived through inversion based on probe sets each arranged in a square点声源/(m,m) 左探头簇反演 右探头簇反演 双探头簇反演 反演位置/(m,m) 定位误差/m 相对误差/% 反演位置/(m,m) 定位误差/m 相对误差/% 反演位置/(m,m) 定位误差/m 相对误差/% (120,80) (115.12,77.23) 5.61 (4.07,3.46) (122.46,81.51) 2.88 (2.05,1.89) (118.79,79.37) 1.36 (1.01,0.79) (100,75) (96.45,72.78) 4.18 (3.55,2.96) (102.38,76.59) 2.86 (2.38,2.12) (99.42,74.69) 0.66 (0.58,0.41) (80,80) (77.63,78.05) 3.07 (2.96,2.44) (82.57,81.69) 3.08 (3.21,2.11) (80.01,80.01) 0.01 (0.012,0.012) (60,70) (62.28,71.53) 2.75 (3.80,2.19) (58.93,71.06) 1.51 (1.78,1.51) (59.61,71.29) 1.35 (0.65,1.84) 对比多组数据发现，使用单簇正方形探头进行定位时，其结果的定位误差通常控制在5.7 m以下，相对误差一般在4.1%以下。进一步增加一个正方形探头簇可以显著提高定位精度，将定位误差降至1.4 m以下，相对误差也相应降低至1.9%以下。以最大相对误差为例，与双三角探头簇相比，单正方形探头簇的误差精度减少约0.6%，而双正方形探头簇的定位精度则提高了大约1.69%。
3 平面层状结构微震源定位方法
由于矿井岩石材料各层具有不同的物理性质，点声源产生的弹性波在界面处会产生透射和反射，这大大增加了声源反演定位的难度。现有的方法通常采用将层状异质结构通过波速的平均值等效为均质材料，以便进行直线反演。然而，这种等效波速不能完全捕捉到各层之间的差异性，导致最终的反演结果可能会错误地将实际位于S0的点声源定位到S1。特别是在多层结构中，这种误差可能会被进一步放大，从而严重影响定位精度。
3.1 层状结构双三角形微震源反演方法
为了提升层状结构中的反演定位精度，本文采用数值模拟方法，综合分析了各层材料的声波传播速度。特别研究了不同探头布置方式对反演定位精度的影响。如图11所示，本研究以一个三层异质结构为例，其材料层分别由 M1、M2和 M3构成。每层的界面坐标(ya、yb)保持常数，相应的纵波波速分别为 c1、c2和 c3。实验中设置了2组直角三角形探头簇。点声源在模型中的传播路径如图11所示，当弹性波遇到不同材料的界面时，会发生透射，其中水平方向的传播角定义为θi，竖直方向的传播角定义为 δi，其中 i = 1, 2, 3。
![]()
图 11 三层异质结构声源路径反演Figure 11. Inversion for paths of an acoustic source in a three-layered heterogeneous structure反演路径在M2与M3界面处的坐标(xb，yb)由下式得出：
$$ {x_{\text{b}}} = \frac{{{y_b} - {y_a}}}{{\tan {\theta _2}}} + {x_a} $$ (11) 3.2 层状异质结构的定位仿真方法
虽然各层材料不同，但在每一层结构均为各向同性的情况下，仍可采用二维模型进行分析，如图12所示，模型尺寸为长200 m，高100 m，四周边界各取10 m低反射虚拟域。根据材料性质将模型分为三层，材料界面y方向高度分别为30 m和70 m，各层材料参数见表6，材料边界设置为材料不连续，由波速方程控制，探头布置如图12所示。材料不连续界面波速控制方程为：
![]()
图 12 层状异质结构数值模拟模型Figure 12. Numerical simulation model for the layered heterogeneous structure表 6 平面三层异质材料波速模型物性参数Table 6. Physical parameters of the velocity model for planar three-layered heterogeneous materials材料属性 密度ρ/(kg·m−3) P波波速/(m·s−1) 均匀波速/(m·s−1) 泥岩 2 520 3 200 3 217 砂岩 2 450 3 850 煤层 1 440 2 600 $$ {c_{{\text{dwon}}}} - {c_{{\text{up}}}} = 0 $$ (12) 模型网格划分采用四边形映射方式，并通过控制网格单元大小进行优化。最大单元的尺寸依据最小波速材料控制，具体参考式(7)。
3.3 平面层状结构探头簇布置及微震源反演定位结果分析
3.3.1 点声源在三层异质结构中的传播
图13显示点声源(120,80)在0.09 s时产生的弹性波波阵面，可观察到弹性波经过材料界面时有显著的反射和透射现象产生，这表明仿真结果与实际物理现象更加接近，同时为后续的反演计算提供可靠的依据。
![]()
图 13 点声源弹性波阵面(0.09 s)Figure 13. Elastic wave front of a acoustic point source (0.09 s)图14展示了各个探头接收到的弹性波特征。通过分析首波(纵波)波峰的到达时间，计算出各探头的时差信息，从而为后续的反演定位提供关键支持。
3.3.2 多结构探头反演定位效果对比分析
在反演过程中，通过读取探头监测到的首波到时见表7，计算所需的时差信息以进行反演分析。其中，材料边界位置ya=30，yb=70。
表 7 探头位置坐标及首波到时实际监测数据Table 7. Probe coordinates and actual monitoring data of first arrival times微震探头 R1 R2 R3 R4 R5 R6 R7 R8 坐标信息/(m,m) (30,15) (30,20) (35,20) (35,15) (160,15) (160,20) (165,20) (165,15) 首波时间/s 0.093 34 0.091 68 0.090 54 0.092 22 0.083 60 0.081 77 0.082 57 0.084 36 通过采用直线反演法、均速反演法和透射反演法分别进行定位计算，得到的定位结果如图15所示。通过改变点声源位置进行多次仿真研究，对比不同反演方法的效果，表8展示了均速反演法与透射反演法的结果对比。
![]()
图 15 透射反演与直线反演结果对比Figure 15. Comparison of source locations derived through transmission and linear inversions对比多组数据发现，采用双三角探头簇的均速算法误差整体控制在18.6 m以下，且相对误差在19.8%以下；而采用透射反演算法时，误差可降低至3.9 m以内，相对误差在4.8%以下，相比于均速反演，透射反演整体定位精度提高了15%。对于双正方形探头簇，均速反演法的定位误差在12.2 m以内，且相对误差在17.0%以下，而透射反演法则将误差降至1.5 m以内，相对误差在2.1%以下，整体定位精度相比均速反演提高了14.9%。
4 三维层状结构微震源反演定位方法
在层状结构呈现各向异性的情况下，二维模型将不再适用，必须采用三维模型进行分析。在三维层状结构中，声波在不同物性材料的异质界面上会产生反射、透射和衍射现象。
表 8 平面三层异质材料不同反演方式定位结果Table 8. Locations of acoustic point sources in planar three-layered heterogeneous materials derived using different inversion methods点声源/
(m,m)均速反演 透射反演 双三角形探头簇 双正方形探头簇 双三角形探头簇 双正方形探头簇 反演位置/
(m,m)定位
误差/m相对
误差/%反演位置/
(m,m)定位
误差/m相对
误差/%反演位置/
(m,m)定位
误差/m相对
误差/%反演位置/
(m,m)定位
误差/m相对
误差/%(120,80) (110.26,95.80) 18.56 (8.12,19.75) (115.35,89.14) 10.25 (3.88,11.43) (120.71,76.18) 3.88 (0.59,4.78) (119.76,78.52) 1.50 (0.20,1.85) (100,80) (92.81,94.21) 15.93 (7.19,17.76) (93.54,88.26) 10.48 (6.46,10.33) (98.24,77.84) 2.78 (1.76,2.70) (100.81,79.19) 1.15 (0.81,1.01) (80,75) (72.65,83.25) 11.05 (9.19,11.0) (74.92,82.64) 9.17 (6.35,10.19) (81.04,76.38) 1.73 (1.30,1.84) (80.93,75.74) 1.19 (1.16,0.99) (60,75) (53.34,85.16) 12.15 (11.1,13.55) (55.35,82.28) 8.64 (7.75,9.71) (59.25,77.16) 2.28 (1.25,2.88) (60.48,75.90) 1.02 (0.80,1.20) (50,80) (43.28,93.81) 15.36 (13.4,17.26) (41.52,91.29) 12.14 (16.96,14.11) (50.65,78.43) 1.70 (1.30,1.96) (48.98,79.82) 1.04 (2.04,0.23) 4.1 三维层状结构微震源反演方法
在三维层状结构中，探头需布置成立体结构以适应空间复杂性。如图16所示，探头在笛卡尔坐标系中布置成一个四面体结构，其中3个面形成直角三角形。以探头R4作为坐标原点，其余3个探头分别位于3个坐标轴上，与原点(R4)的距离均为d。声源S的坐标为 (xS，yS，zS)。探头Ri的坐标为(xi，yi，zi)，其中 i = 1, 2, 3, 4。另一组探头以R8为原点进行类似布置。
![]()
图 16 三维层状结构微震源透射反演Figure 16. Transmission inversion for a microseismic source in a three-dimensional layered structure在整个探头簇位于同一材料中时，接收到的弹性波波速是一致的，探头之间的相对位置信息可以通过时差信息来确定。通过空间中2条反演直线交点，可确定点声源的位置。
以两层异质介质为例，在已知界面平面za的情况下，声波传播轨迹在材料界面上的交点坐标定为(zatan$ {\delta }_{x{\textit{z}}} $，zatan$ {\delta }_{y{\textit{z}}} $，za)，如图16所示。该交点坐标随后可作为反演起点进行进一步分析。
$$ \left\{\begin{aligned} & {x_S} = \frac{{{x_8}\tan {\delta _{xy}} - 2{x_8}\tan {\beta _{xy}} + {y_4}\tan {\delta _{xy}} + {x_8} - {x_4}}}{{\tan {\delta _{xy}} - \tan {\beta _{xy}}}} \\ & {y_S} = \frac{{{y_4}\tan {\delta _{xy}} - {y_8}\tan {\beta _{xy}} + {x_8} - {x_4}}}{{\tan {\delta _{xy}} - \tan {\beta _{xy}}}} \\ & {{\textit{z}}_S} = \frac{{{{\textit{z}}_8}\tan {\beta _{y{\textit{z}}}} - {y_4}\tan {\delta _{y{\textit{z}}}} + {y_4} - {y_8}}}{{\tan {\beta _{y{\textit{z}}}} - \tan {\delta _{y{\textit{z}}}}}}\end{aligned} \right. $$ (13) 4.2 三维层状结构的定位仿真方法
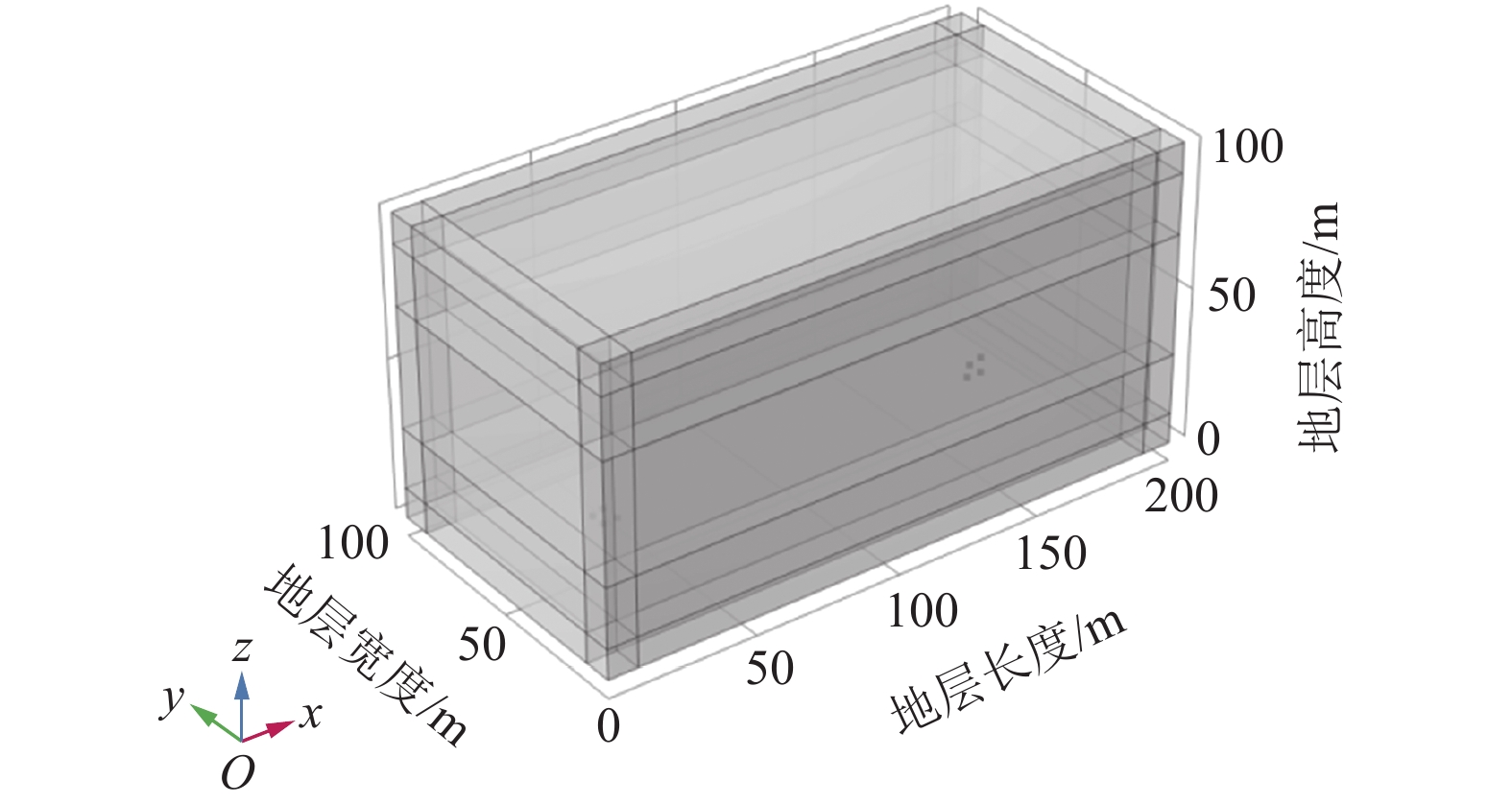
建立了一个长200 m，宽100 m，高100 m的三维空间地层模型，如图17所示，模型边界设置为10 m厚的低反射虚拟域，并划分为三层结构，材料界面z方向的高度分别为30 m和70 m，设置了8个监测探头。各层材料参数见表6，材料边界设为不连续，由波速方程控制。
![]()
图 17 三维层状结构数值模拟模型Figure 17. Numerical model for the three-dimensional layered structure点声源的空间分布控制方程由下式表示：
$$ \begin{aligned} &\text{Gspace}(x,y)=\\ &A{\left\{(\text{πd}S)\mathrm{exp}\left[\frac{-({(x-{x}_{0})}^{2}+{(y-{y}_{0})}^{2}+{({\textit{z}}-{{\textit{z}}}_{0})}^{2}}{\text{d}V}\right]\right\}}^{-1} \end{aligned}$$ (14) 图18为点声源空间分布函数的切片，显示出点声源在空间中呈现出球状分布。
![]()
图 18 点声源激励空间函数分布Figure 18. Spatial function distribution of acoustic point source excitation点声源的时间函数控制参考式(6)，其中时间延时t0取0.02 s，网格模型采用自动扫掠生成正六面体单元，最大单元尺寸由已知材料的最小波速控制，参照式(7)。
4.3 三维层状结构探头布置及微震源反演定位结果分析
4.3.1 点声源在三维结构中的传播
该模型通过总振动来表征弹性波的传播过程。在0.02 s时，由于点激励作用，形成了一个球状高亮点声源；到0.062 s时，可以观察到弹性波在三层空间结构中的传播情况。在其xz平面的切片图中，明显可以看到弹性波在材料界面处产生了显著的反射和透射现象，如图19所示。
探头放置在点R1—R8处，形成2个四面体探头簇，用来接收记录来自点声源的弹性波信息。图20显示了各个探头位移监测得到的波形图。通过分析首波(纵波)波峰的到达时间，计算探头的时差信息，为后续的反演计算提供了重要依据。
4.3.2 多结构探头反演定位效果对比分析
四面体探头的布置位置及其监测数据见表9，其中材料边界位置为za=30，zb=70。
表 9 四面体探头布置坐标及首波到时实际监测数据Table 9. Coordinates of probe sets each arranged in a tetrahedron and actual monitoring data of first arrival times探头 R1 R2 R3 R4 R5 R6 R7 R8 坐标/(m,m) (35,45,15) (30,50,15) (30,45,20) (30,45,15) (165,45,15) (165,45,20) (165,50,15) (160,45,15) 首波/s 0.048 80 0.049 48 0.048 34 0.049 87 0.041 02 0.041 17 0.040 02 0.041 70 基于仿真得到的时差信息，本研究分别采用均速反演和透射反演法来确定点声源的位置，图21展示了当点声源位于坐标(120, 80, 80)时，四面体探头簇对点声源进行透射和均速反演的结果。误差计算采用下式，通过比较点声源的预测位置与实际位置之间的距离来进行。通过改变声源点的位置，得到了不同反演方法的结果及其误差，详见表10。
![]()
图 21 三维层状结构均速、透射反演结果对比Figure 21. Comparison of locations of a acoustic point source in a three-dimensional layered structure derived through uniform velocity and transmission inversions$$ \Delta L = \sqrt {{{({x_S} - {x_i})}^2} + {{({y_S} - {y_i})}^2} + {{({{\textit{z}}_S} - {{\textit{z}}_i})}^2}} $$ (15) 定位结果显示，当忽略岩层材料界面透射的影响时，使用传统的均速反演方法得到的点声源定位结果与实际点源存在较大误差。然而，若优化反演方法，并在材料边界处充分考虑由波速差异导致的透射影响，定位精度将显著提高。通过对比多组数据可知，使用三维模型的均速算法，误差整体控制在12.9 m以下，相对误差在16.6%以下。而采用透射反演算法时，误差整体可减少至2.3 m以下，相对误差也降至2.1%以下。这表明，与传统的经验均速算法相比，透射算法在三维层状结构中可以将定位精度提高约14.5%。
表 10 空间三层异质材料的均速、透射点声源反演定位结果Table 10. Locations of acoustic point sources in three-dimensional layered heterogeneous materials derived through uniform velocity and transmission inversions均速反演法 透射反演法 点声源坐标 定位值 误差/m 相对误差/% 定位值 误差/m 相对误差/% (120,80,80) (111.40,72.81,73.62) 12.90 (7.17,8.99,7.98) (118.62,78.57,81.14) 2.29 (1.15,1.79,1.43) (90,50,75) (82.53,41.72,69.88) 12.27 (8.30,16.56,6.83) (88.79,49.62,73.94) 1.65 (1.34,0.76,1.41) (60,60,80) (55.82,53.91,76.64) 8.11 (6.97,10.15,4.20) (58.75,59.03,78.89) 1.93 (2.08,1.61,1.39) 5 结 论
(1)通过有限元法模拟了弹性波在不同地层结构中的传播过程，研究了不同探头布置方式及反演模型对微震源定位精度的影响，并提出了优化矿井微震监测预警系统的方案。
(2)正交探头布置在声源定位中的表现优于其他探头布置方式，尤其在平面均质材料和三维层状结构中，双正方形探头簇和直角四面体探头簇的定位精度有显著提升，进一步表明探头布置的合理性对声源定位至关重要。
(3)采用透射反演模型在复杂地层结构中表现更为优越，特别是在平面层状和三维层状结构中，正交探头透射反演法比均速反演法在精度上分别提升了14.9%和14.5%。这表明反演模型的选择对声源定位的精度起着关键作用。
(4)方法的适用性与计算效率：有限元仿真方法不仅能够有效模拟不同地层结构中的弹性波传播，还在不影响精度的前提下，实现了较高的计算效率。这为矿井微震和微震监测提供了理论支持，尤其是在快速计算与复杂地层环境中，具备较强的适应性。
符号注释：
A为激励峰值系数； c为弹性波速度，m/s；cp为点声源在传播介质中的纵波波速，m/s；cSmin为横波波速最小值，m/s；Cup、Cdown分别为界面上方、下方的波速，m/s；dS为点声源激励面积，取(120，80)；dV为点声源激励空间体积；E为材料的弹性模量，Pa；Lmax为最大网格单元大小，m；ti为纵波到达探头i的时间，s；ρ为材料密度，kg/m3；$ \mu $为材料泊松比；(xs, ys, zs)为微震源坐标，xi、yi、zi(i=1，2，···，8)，分别为各探头坐标；(x0，y0，z0)为点声源坐标，本次示例取值为(120, 80, 80)；δ为声源到探头传播路径在各个平面上的投影与其他探头在相应平面上投影之间的夹角。
-
![]()
图 1 直角三角形探头簇微震源反演
Fig. 1 Inversion for a microseismic source based on two probe sets each arranged in an right triangle
![]()
图 2 正方形探头簇微震源反演
Fig. 2 Inversion for a microseismic source based on a probe set arranged in a square
![]()
图 5 点声源激励时间函数及其频谱分布
Fig. 5 Time function of acoustic point source excitation and its frequency spectrum
![]()
图 6 不同时刻点声源位于(120,80)处弹性波阵面
Fig. 6 Elastic wave fronts of an acoustic point source at (120, 80) under varying times
![]()
图 10 双正方形探头反演结果
Fig. 10 Inversion results based on double probe sets each arranged in a square
![]()
图 11 三层异质结构声源路径反演
Fig. 11 Inversion for paths of an acoustic source in a three-layered heterogeneous structure
![]()
图 12 层状异质结构数值模拟模型
Fig. 12 Numerical simulation model for the layered heterogeneous structure
![]()
图 15 透射反演与直线反演结果对比
Fig. 15 Comparison of source locations derived through transmission and linear inversions
![]()
图 16 三维层状结构微震源透射反演
Fig. 16 Transmission inversion for a microseismic source in a three-dimensional layered structure
![]()
图 18 点声源激励空间函数分布
Fig. 18 Spatial function distribution of acoustic point source excitation
![]()
图 21 三维层状结构均速、透射反演结果对比
Fig. 21 Comparison of locations of a acoustic point source in a three-dimensional layered structure derived through uniform velocity and transmission inversions
表 1 均质平面结构波速模型物性参数
Table 1 Physical parameters of the velocity model for a homogeneous planar structure
材料属性 密度ρ/(kg·m−3) P波波速cP/(m·s−1) S波波速cS/(m·s−1) 砂岩 2520 3850 2082 
下载: 导出CSV
表 2 探头布置坐标及首波到时实际监测数据
Table 2 Probe coordinates and actual monitoring data of first arrival times
微震探头 R1 R2 R3 R4 R5 R6 R7 R8 坐标/(m,m) (30,15) (30,20) (35,20) (35,15) (160,15) (160,20) (165,20) (165,15) 首波时间/s 0.089 88 0.089 02 0.087 96 0.088 76 0.080 90 0.079 79 0.080 53 0.081 60
下载: 导出CSV
表 3 计算获得的各探头时差信息
Table 3 Calculated differences in the arrival times at various probes
时差 Δt12 Δt23 Δt34 Δt41 Δt56 Δt67 Δt78 Δt85 计算值/s 0.00086 0.00106 0.0008 0.00112 0.00111 0.00074 0.00179 0.0007
下载: 导出CSV
表 4 平面均匀材料的双三角探头点声源反演定位结果
Table 4 Locations of acoustic point sources in planar homogeneous materials derived through inversion based on probe sets arranged in double triangles
点声源坐标/(m,m) 双三角探头簇
反演位置/(m,m)定位误差/m 相对误差/% (120,80) (118.16,82.76) 3.32 (1.53,3.45) (100,70) (98.52,71.81) 2.34 (1.48,2.59) (80,80) (81.02,78.84) 1.54 (1.28,1.45) (60,70) (61.37,71.21) 1.83 (2.28,1.73) (50,60) (51.56,58.97) 1.87 (3.12,1.72)
下载: 导出CSV
表 5 平面均质材料的正方形探头点声源反演定位结果
Table 5 Locations of acoustic point sources in planar homogeneous materials derived through inversion based on probe sets each arranged in a square
点声源/(m,m) 左探头簇反演 右探头簇反演 双探头簇反演 反演位置/(m,m) 定位误差/m 相对误差/% 反演位置/(m,m) 定位误差/m 相对误差/% 反演位置/(m,m) 定位误差/m 相对误差/% (120,80) (115.12,77.23) 5.61 (4.07,3.46) (122.46,81.51) 2.88 (2.05,1.89) (118.79,79.37) 1.36 (1.01,0.79) (100,75) (96.45,72.78) 4.18 (3.55,2.96) (102.38,76.59) 2.86 (2.38,2.12) (99.42,74.69) 0.66 (0.58,0.41) (80,80) (77.63,78.05) 3.07 (2.96,2.44) (82.57,81.69) 3.08 (3.21,2.11) (80.01,80.01) 0.01 (0.012,0.012) (60,70) (62.28,71.53) 2.75 (3.80,2.19) (58.93,71.06) 1.51 (1.78,1.51) (59.61,71.29) 1.35 (0.65,1.84)
下载: 导出CSV
表 6 平面三层异质材料波速模型物性参数
Table 6 Physical parameters of the velocity model for planar three-layered heterogeneous materials
材料属性 密度ρ/(kg·m−3) P波波速/(m·s−1) 均匀波速/(m·s−1) 泥岩 2 520 3 200 3 217 砂岩 2 450 3 850 煤层 1 440 2 600
下载: 导出CSV
表 7 探头位置坐标及首波到时实际监测数据
Table 7 Probe coordinates and actual monitoring data of first arrival times
微震探头 R1 R2 R3 R4 R5 R6 R7 R8 坐标信息/(m,m) (30,15) (30,20) (35,20) (35,15) (160,15) (160,20) (165,20) (165,15) 首波时间/s 0.093 34 0.091 68 0.090 54 0.092 22 0.083 60 0.081 77 0.082 57 0.084 36
下载: 导出CSV
表 8 平面三层异质材料不同反演方式定位结果
Table 8 Locations of acoustic point sources in planar three-layered heterogeneous materials derived using different inversion methods
点声源/
(m,m)均速反演 透射反演 双三角形探头簇 双正方形探头簇 双三角形探头簇 双正方形探头簇 反演位置/
(m,m)定位
误差/m相对
误差/%反演位置/
(m,m)定位
误差/m相对
误差/%反演位置/
(m,m)定位
误差/m相对
误差/%反演位置/
(m,m)定位
误差/m相对
误差/%(120,80) (110.26,95.80) 18.56 (8.12,19.75) (115.35,89.14) 10.25 (3.88,11.43) (120.71,76.18) 3.88 (0.59,4.78) (119.76,78.52) 1.50 (0.20,1.85) (100,80) (92.81,94.21) 15.93 (7.19,17.76) (93.54,88.26) 10.48 (6.46,10.33) (98.24,77.84) 2.78 (1.76,2.70) (100.81,79.19) 1.15 (0.81,1.01) (80,75) (72.65,83.25) 11.05 (9.19,11.0) (74.92,82.64) 9.17 (6.35,10.19) (81.04,76.38) 1.73 (1.30,1.84) (80.93,75.74) 1.19 (1.16,0.99) (60,75) (53.34,85.16) 12.15 (11.1,13.55) (55.35,82.28) 8.64 (7.75,9.71) (59.25,77.16) 2.28 (1.25,2.88) (60.48,75.90) 1.02 (0.80,1.20) (50,80) (43.28,93.81) 15.36 (13.4,17.26) (41.52,91.29) 12.14 (16.96,14.11) (50.65,78.43) 1.70 (1.30,1.96) (48.98,79.82) 1.04 (2.04,0.23)
下载: 导出CSV
表 9 四面体探头布置坐标及首波到时实际监测数据
Table 9 Coordinates of probe sets each arranged in a tetrahedron and actual monitoring data of first arrival times
探头 R1 R2 R3 R4 R5 R6 R7 R8 坐标/(m,m) (35,45,15) (30,50,15) (30,45,20) (30,45,15) (165,45,15) (165,45,20) (165,50,15) (160,45,15) 首波/s 0.048 80 0.049 48 0.048 34 0.049 87 0.041 02 0.041 17 0.040 02 0.041 70
下载: 导出CSV
表 10 空间三层异质材料的均速、透射点声源反演定位结果
Table 10 Locations of acoustic point sources in three-dimensional layered heterogeneous materials derived through uniform velocity and transmission inversions
均速反演法 透射反演法 点声源坐标 定位值 误差/m 相对误差/% 定位值 误差/m 相对误差/% (120,80,80) (111.40,72.81,73.62) 12.90 (7.17,8.99,7.98) (118.62,78.57,81.14) 2.29 (1.15,1.79,1.43) (90,50,75) (82.53,41.72,69.88) 12.27 (8.30,16.56,6.83) (88.79,49.62,73.94) 1.65 (1.34,0.76,1.41) (60,60,80) (55.82,53.91,76.64) 8.11 (6.97,10.15,4.20) (58.75,59.03,78.89) 1.93 (2.08,1.61,1.39)
下载: 导出CSV
-
[1] 尹尚先,徐斌,尹慧超,等. 矿井水防治学科基本架构及内涵[J]. 煤炭科学技术,2023,51(7):24−35. YIN Shangxian,XU Bin,YIN Huichao,et al. Basic structure and connotation of mine water prevention and control discipline[J]. Coal Science and Technology,2023,51(7):24−35.
[2] 刘其声. 关于突水系数的讨论[J]. 煤田地质与勘探,2009,37(4):34−37. DOI: 10.3969/j.issn.1001-1986.2009.04.009 LIU Qisheng. A discussion on water inrush coefficient[J]. Coal Geology & Exploration,2009,37(4):34−37. DOI: 10.3969/j.issn.1001-1986.2009.04.009
[3] 武强. 煤矿防治水细则解读[M]. 北京:煤炭工业出版社,2018. [4] 尹尚先,连会青,徐斌,等. 深部带压开采:传承与创新[J]. 煤田地质与勘探,2021,49(1):170−181. DOI: 10.3969/j.issn.1001-1986.2021.01.018 YIN Shangxian,LIAN Huiqing,XU Bin,et al. Deep mining under safe water pressure of aquifer:Inheritance and innovation[J]. Coal Geology & Exploration,2021,49(1):170−181. DOI: 10.3969/j.issn.1001-1986.2021.01.018
[5] 丁湘,申斌学,郑忠友,等. 深部侏罗系矿井充水强度评价与水害风险管控[M]. 北京:应急管理出版社,2022. [6] 张文泉,王在勇,吴欣焘,等. 顶板离层水突涌模式及预防技术模拟研究[J]. 煤田地质与勘探,2021,49(1):217−224. DOI: 10.3969/j.issn.1001-1986.2021.01.023 ZHANG Wenquan,WANG Zaiyong,WU Xintao,et al. Investigation and simulation on the model and prevention technology of water inrush from roof bed separation[J]. Coal Geology & Exploration,2021,49(1):217−224. DOI: 10.3969/j.issn.1001-1986.2021.01.023
[7] LU Caiping,DOU Linming,ZHANG Nong,et al. Microseismic and acoustic emission effect on gas outburst hazard triggered by shock wave:A case study[J]. Natural Hazards,2014,73(3):1715−1731. DOI: 10.1007/s11069-014-1167-7
[8] KOERNER R M,LORD A E JR. Application of acoustic emission in the geotechnical area[J]. The Journal of the Acoustical Society of America,1978,64(Sup.1):S175.
[9] DONG Longjun,ZOU Wei,LI Xibing,et al. Collaborative localization method using analytical and iterative solutions for microseismic/acoustic emission sources in the rockmass structure for underground mining[J]. Engineering Fracture Mechanics,2019,210:95−112. DOI: 10.1016/j.engfracmech.2018.01.032
[10] SURDI A A,EKART D D,DURAN P,et al. Possible sources of acoustic emission events during hydraulic fracturing[C]//The 44th U. S. Rock Mechanics Symposium and 5th U. S. –Canada Rock Mechanics Symposium. Salt Lake City,2010:ARMA-10-478.
[11] SCOTT T E JR,ZENG Zhengwen,ROEGIERS J C. Acoustic emission imaging of induced asymmetrical hydraulic fractures[C]//The 4th North American Rock Mechanics Symposium. Seattle,2000:ARMA-2000-2129.
[12] GHOSH A,HSIUNG S M. Acoustic emission as an indicator of macrofailure of rock[C]//The 4th North American Rock Mechanics Symposium. Seattle,2000:ARMA-2000-1135.
[13] HAMPTON J,FRASH L,GUTIERREZ M. Investigation of laboratory hydraulic fracture source mechanisms using acoustic emission[C]//The 47th U. S. Rock Mechanics/Geomechanics Symposium. San Francisco,2013:ARMA-2013-315.
[14] BUNGER A P,KEAR J,DYSKIN A V,et al. Interpreting post–injection acoustic emission in laboratory hydraulic fracturing experiments[C]//The 48th U. S. Rock Mechanics/Geomechanics Symposium. Minneapolis,2014:ARMA-2014-6973.
[15] STANCHITS S,BURGHARDT J,SURDI A,et al. Acoustic emission monitoring of heterogeneous rock hydraulic fracturing[C]//The 48th U. S. Rock Mechanics/Geomechanics Symposium. Minneapolis,2014:ARMA-2014-7775.
[16] MOLENDA M,STÖCKHERT F,BRENNE S,et al. Acoustic emission monitoring of laboratory scale hydraulic fracturing experiments[C]//The 49th U. S. Rock Mechanics/Geomechanics Symposium. San Francisco,2015:ARMA-2015-069.
[17] NOMIKOS P P,SAKKAS K M,SOFIANOS A I. Acoustic emission of Dionysos marble specimens in uniaxial compression[C]//The 12th ISRM Congress. Beijing,2011:ARMA-12CONGRESS-2011-132.
[18] KANG Y M. Acoustic emission signal processing based on wavelet analysis[C]//The ISRM International Symposium–5th Asian Rock Mechanics Symposium. Tehran,2008:ISRM-ARMSS-2008-037.
[19] XIE Qiang,ZHANG Yongxing,YU Xianbin. Study on acoustic emission of limestone in uniaxial compression test[J]. Journal of Civil and Environmental Engineering,2002,24(1):19.
[20] TUOKKO T,POUTANEN M S. Acoustic emission based rock stress measurement method[C]//The ISRM Regional Symposium–EUROCK 2009. Cavtat,2009:ISRM-EVROCK-2010-061.
[21] SLATALLA N,ALBER M. Characteristic acoustic emission response of sandstone samples in uniaxial compression[C]//The ISRM International Symposium–EUROCK 2010. Lausanne,2010:ISRM-EVROCK-2010-013.
[22] TAVALLALI A,VERVOORT A. Acoustic emission monitoring of layered sandstone under Brazilian test conditions[C]//The ISRM International Symposium–EUROCK 2010. Lausanne,2010:ISRM-EVROCK-2010-015.
[23] 杨健,王连俊. 岩爆机理声发射试验研究[J]. 岩石力学与工程学报,2005,24(20):3796−3802. DOI: 10.3321/j.issn:1000-6915.2005.20.031 YANG Jian,WANG Lianjun. Study on mechanism of rock burst by acoustic emission testing[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(20):3796−3802. DOI: 10.3321/j.issn:1000-6915.2005.20.031
[24] CHEN Z H,TANG C A,HUANG R Q. A double rock sample model for rockbursts[J]. International Journal of Rock Mechanics and Mining Sciences,1997,34(6):991−1000. DOI: 10.1016/S1365-1609(97)80008-1
[25] MARTIN C D,CHRISTIANSSON R C. Overcoring in highly stressed granite:Comparison of USBM and modified CSIR devices[J]. Rock Mechanics and Rock Engineering,1991,24(4):207−235. DOI: 10.1007/BF01045032
[26] HARMON L,WEIR J T,BROCK C D,et al. GEIGER:Investigating evolutionary radiations[J]. Bioinformatics,2008,24(1):129−131. DOI: 10.1093/bioinformatics/btm538
[27] 孔韩东,边银菊,刘瑞丰,等. 地震定位方法研究进展[J]. 地震地磁观测与研究,2017,38(4):81−92. DOI: 10.3969/j.issn.1003-3246.2017.04.014 KONG Handong,BIAN Yinju,LIU Ruifeng,et al. Review of seismic location study[J]. Seismological and Geomagnetic Observation and Research,2017,38(4):81−92. DOI: 10.3969/j.issn.1003-3246.2017.04.014
[28] 陈炳瑞,冯夏庭,李庶林,等. 基于粒子群算法的岩体微震源分层定位方法[J]. 岩石力学与工程学报,2009,28(4):740−749. DOI: 10.3321/j.issn:1000-6915.2009.04.012 CHEN Bingrui,FENG Xiating,LI Shulin,et al. Microseism source location with hierarchical strategy based on particle swarm optimization[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(4):740−749. DOI: 10.3321/j.issn:1000-6915.2009.04.012
[29] 王辉,梁苗,朱梦博. 基于单纯形–最短路径射线追踪的微震震源混合定位算法[J]. 中国矿业,2020,29(10):110−115. DOI: 10.12075/j.issn.1004-4051.2020.10.011 WANG Hui,LIANG Miao,ZHU Mengbo. A hybrid microseismic source location algorithm based on simplex and shortest path ray tracing[J]. China Mining Magazine,2020,29(10):110−115. DOI: 10.12075/j.issn.1004-4051.2020.10.011
[30] 黄晓红,孙国庆,张凯月,等. 基于多次互相关和Geiger算法的声发射源定位研究[J]. 矿业研究与开发,2016,36(7):77−81. HUANG Xiaohong,SUN Guoqing,ZHANG Kaiyue,et al. Research on source location of acoustic emission based on multiple cross correlation and Geiger algorithm[J]. Mining Research and Development,2016,36(7):77−81.
[31] 林峰,李庶林,薛云亮,等. 基于不同初值的微震源定位方法[J]. 岩石力学与工程学报,2010,29(5):996−1002. LIN Feng,LI Shulin,XUE Yunliang,et al. Microseismic sources location methods based on different initial values[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(5):996−1002.
[32] 赵勇胜,赵拥军,赵闯. 联合角度和时差的单站无源相干定位加权最小二乘算法[J]. 雷达学报,2016,5(3):302−311. ZHAO Yongsheng,ZHAO Yongjun,ZHAO Chuang. Weighted least squares algorithm for single–observer passive coherent location using DOA and TDOA measurements[J]. Journal of Radars,2016,5(3):302−311.
[33] YU Huagang,HUANG Gaoming,GAO Jun,et al. Practical constrained least–square algorithm for moving source location using TDOA and FDOA measurements[J]. Journal of Systems Engineering and Electronics,2012,23(4):488−494. DOI: 10.1109/JSEE.2012.00062
[34] 李楠,王恩元,孙珍玉,等. 基于L1范数统计的单纯形微震震源定位方法[J]. 煤炭学报,2014,39(12):2431−2438. LI Nan,WANG Enyuan,SUN Zhenyu,et al. Simplex microseismic source location method based on L1 norm statistical standard[J]. Journal of China Coal Society,2014,39(12):2431−2438.
[35] 尹莘新. 基于时差法的声发射源定位方法研究[D]. 长春:吉林大学,2020. YIN Shenxin. Study of acoustic source localization techniques based on TDOA[D]. Changchun:Jilin University,2020.
[36] 尹莘新,崔志文,吕伟国. 二维板声发射源定位实验的一种简易实现方法[J]. 大学物理,2017,36(8):30−35. YIN Shenxin,CUI Zhiwen,LYU Weiguo. A simple experimental method of 2D acoustic source localization[J]. College Physics,2017,36(8):30−35.
[37] 崔志文,尹莘新. 适用于三维结构的声发射源定位方法:CN111239256A[P]. 2020-06-05. [38] GHOSE B,BALASUBRAMANIAM K,KRISHNAMURTHY C V,et al. Two–dimensional FEM simulation of ultrasonic wave propagation in isotropic solid media using COMSOL[C]//The COMSOL Conference. India,2010.
计量
- 文章访问数: 64
- HTML全文浏览量: 8
- PDF下载量: 16
