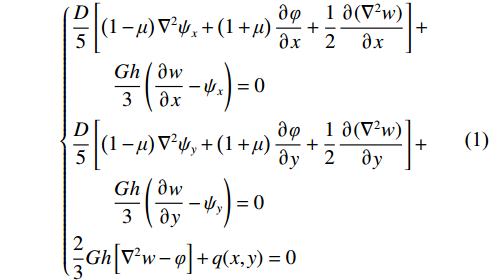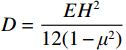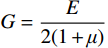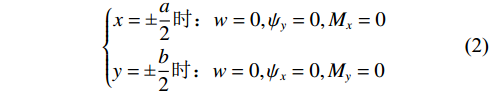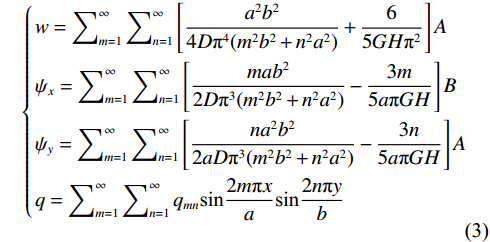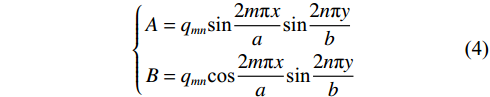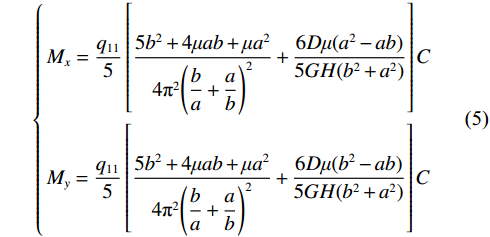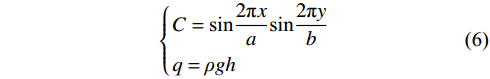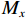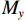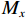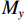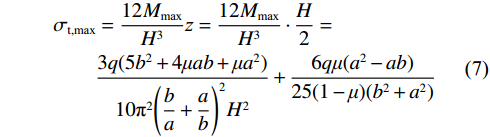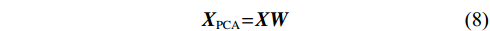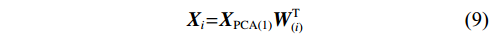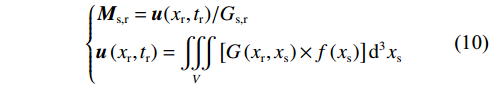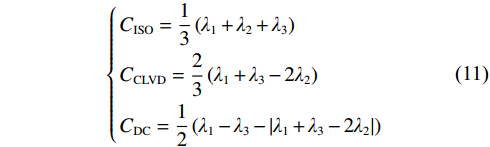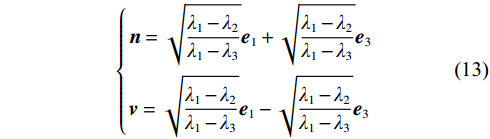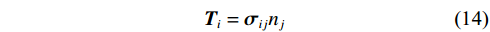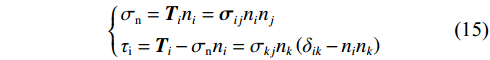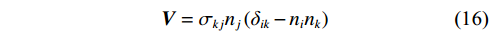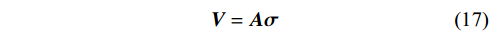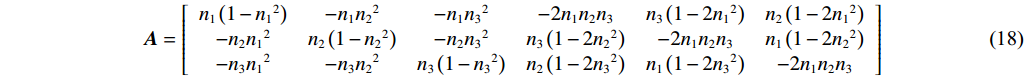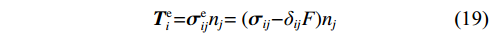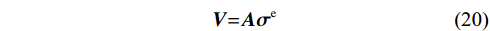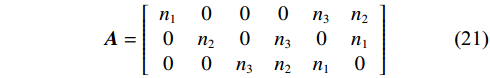Fracturing characteristics of significantly thick overburden inducing mine earthquakes and the stress-triggering mechanisms of the mine earthquakes
-
摘要:目的
深部开采巨厚覆岩破断导致引起地表震感的矿震频发，已成为制约矿区高效生产的最严峻难题，亟待改变矿区巨厚覆岩矿震频度高、防控难现状。
方法以内蒙古自治区鄂尔多斯呼吉尔特矿区某邻空综采工作面频发巨厚覆岩矿震为研究对象，应用厚板理论分析巨厚覆岩结构破断演化规律，提取矿震波形主成分并采用矩张量反演方法定量研究矿震震源破裂机制，基于张拉、压缩及混合破裂震源主应力作用方式修正应力反演模型，改进应力反演算法，分析矿震震源孕育破裂特征及应力场演化规律，定量解析矿震应力触发机制。
结果和结论结果表明，巨厚覆岩破断运移为矿震孕育触发的动力、能量源；主成分分析方法可快速提取因采矿环境干扰波形的主成分，为矩张量求解提供优质反演数据；修正后应力反演算法能够满足采动诱发非剪切破裂震源应力反演需求，实现对典型张拉、压缩等非剪切破裂矿震震源应力场反演；工作面邻空回采期间，顶板逐层向上与侧向采空区联动破断，采空区影响使得孕震期间顶板活动性增强，巨厚覆岩断裂特征整体呈显著张拉状态；矿震孕育过程中主应力作用方位基本一致，应力形因子分别为0.66、0.71和0.30，覆岩应力分布由单轴挤压转变为挤压张拉状态，最大主应力单轴挤压作用导致巨厚覆岩瞬时断裂释放大量弹性能是诱发“2·6”和“10·30”矿震的主要原因，工作面邻更大范围采空区开采，最大、最小主应力挤压张拉协同作用将可能诱发更大能级矿震。研究结论可为矿区及周边因矿震问题限制高效生产的矿井从源头调控降载减震提供理论支撑。
Abstract:ObjectiveFrequent mine earthquakes that cause surface seismaesthesia, induced by the fracturing of significantly thick overburden in deep coal mining, are identified as the most severe challenge to the efficient production of mining areas. There is an urgent need to overcome the current difficulty caused by mine earthquakes induced by significantly thick overburden, which feature high frequency and challenging prevention and control.
MethodsUsing such mine earthquakes occurring in a certain fully mechanized mining face adjacent to goaves in the Khujirt mining area in Ordos, Inner Mongolia Autonomous Region, as an example, this study (1) analyzed the evolutionary patterns of structural fracturing of the significantly thick overburden based on the thick plate theory; (2) extracted the principal components of mine earthquake waveforms and quantitatively explored the fracturing mechanisms of seismic sources using the moment tensor inversion method; (3) corrected the stress inversion model and algorithm based on the acting mechanisms of principal stresses acting on seismic sources subjected to tensile, compressive, or mixed-type fracturing; and (4) analyzed the fracturing characteristics of the sources of mine earthquakes and the evolutionary patterns of stress fields and quantitatively analyzed the stress-triggering mechanisms of the mine earthquakes.
Results and ConclusionsThe results indicate that the fracturing and migration of the significantly thick overburden provide impetus and energy for the formation and triggering of mine earthquakes. The principal component analysis method can quickly extract the principal components of the waveforms disturbed by mining environments, thus providing high-quality inversion data for solving the moment tensor. The corrected stress inversion algorithm satisfied the requirements for the stress inversion of seismic sources subjected to mining-induced non-shear fracturing, thus allowing for the inversion of stress fields of typical seismic sources subjected to tensile/compressive fracturing. The mining along the mining face adjacent to goaves caused the roofs, along with lateral goaves, to fracture upwards layer by layer. Under the influence of goaves, the roof activity intensified during the formation of mine earthquakes. The fracturing characteristics of the significantly thick overburden generally manifested a significant tensile state. During the formation of mine earthquakes, principal stresses exhibited roughly consistent orientations, with stress shape factors of 0.66, 0.71, and 0.30. The stress distribution of the overburden transitioned from uniaxial compression to a compressive-tensile state. The uniaxial compression of the maximum principal stress led to the transient fracturing of the significantly thick overburden. This was accompanied by the release of significant elastic energy, which served as the primary cause of the February 6 and October 30, 2021 Hujierte mining area earthquakes. In the case of the mining face adjacent to large goaves, the synergistic effects of compression and tension under the maximum and minimum principal stresses may induce mine earthquakes with higher magnitudes. For mines whose efficient production is restricted by mine earthquakes, the conclusions of this study will provide theoretical support for adjusting loads and reducing mine earthquakes from sources.
-
矿区大规模开发进入深部开采后，可能引起地表出现震感的高能级、大体量矿震活动频发[1]，困扰矿区居民正常生活、严重制约煤炭资源高效生产[2]。以蒙陕深部矿区为例，2020年以来，矿区内先后发生2.0级以上矿震近20次，2024年矿区内矿震再次突增，1个月内红庆河、龙王沟等煤矿陆续发生矿震5次，成为制约矿区高效生产的最严峻难题[3]。矿区主采煤层赋存地层沉积环境复杂，以白垩系志丹群巨厚覆岩与其相邻地层不整合沉积为最典型特征[4]，增大了矿震灾害防控难度[5]。如何深度挖掘震源孕育破裂信息，开展孕震区应力场反演、定量解析矿震应力触发机制是从源头应力调控实现降载减震的关键，更是保障我国西部煤炭资源安全高效开采的重大需求。
矩张量反演方法在采动矿震震源机制研究方面得到了应用，为定量描述煤岩破裂过程、破裂面信息提供了更多途径。深部矿井褶皱、断层构造及高应力煤柱区这3类典型冲击地压频发区，其震源破裂机制存在差异性[6]。应用矩张量反演方法，可获得岩石内部裂纹萌发、孕育、延伸和贯通全过程时空演化机制[7]。利用震源机制解析可判别矿震震动波辐射影响方位，分析巨厚覆岩断裂演化特征[8]。对于顶板破断诱发的矿震震源破裂机制与破裂面参数则具有明显集聚特征[9]。通过引入地应力信息约束矿震震源机制，对比反演与实测破裂信息可验证改进方法的可行性[10]。对于压裂诱发矿震震源破裂面信息难以准确判识，同时因流体再次注入造成地层结构局部改变可能导致更大能级矿震发生[11]。上述研究揭示了矿井常见地层开采条件频发矿震震源破裂机制，但蒙陕矿区巨厚覆岩监测数据少、质量低，震源矩张量求解准确度难以保证，缺乏对矿震孕育过程覆岩破裂演化机制的量化分析。
基于震源机制解析获取的破裂面信息，可实现对采动诱发矿震应力场的快速反演。根据强矿压频发区震源应力场分布特征，可知残余构造应力释放是导致强矿震的原因[12]。基于不规则煤柱冲击破裂机制的反演结果，可揭示主应力对煤柱变形的控制作用[13]。引入不稳定系数和岩体摩擦因数可避免因误判破裂面信息影响应力反演结果[14]。沉积层内频发高能级矿震与局部压应力作用密切相关，同时矿震事件促进了应力状态偏转[15]。联合震源破裂面信息反演应力场演化规律，可进一步识别裂隙扩展发育趋势[16]。引入卡尔曼滤波方法以准确获取破裂面产状信息，进而厘清应力场分布与破裂滑移梯度空间相关性[17]。局部构造应力场决定了采动诱发矿震破裂机制，采动引起应力场变化则大幅提高了矿震频度[18]。以上研究表明获取应力场分布状态对于解析矿震应力触发机制方面具有重要意义，但研究对象以纯剪切破裂震源为主，对于矿山采动矿震震源则存在张拉、压缩及混合破裂模式，上述应力反演方法并不完全适用于反演煤矿复杂环境大量非剪切破裂震源的应力场状态。
综上，笔者以内蒙古自治区鄂尔多斯呼吉尔特矿区某深部邻空开采工作面频发矿震为研究对象，通过主成分分析预处理提取矿震主成分波形，降低煤矿复杂环境对矿震信号的干扰，为求解矿震震源矩张量提供优质反演数据。综合考虑矩张量分量占比情况判识震源破裂类型，结合张拉、压缩及混合破裂震源主应力作用方式修正应力反演模型，以指导改进反演算法使其兼顾煤矿复杂环境大量非剪切破裂震源的应力场反演。在获取震源破裂机制基础上，研究工作面各次矿震孕育过程中覆岩逐层断裂特征，分析覆岩破断诱发矿震震源应力场演化规律，定量解析触发矿震的力学机制，以期为矿区及周边有矿震风险的矿井从源头调控降载减震提供理论支撑。
1 工程背景
1.1 开采地质条件
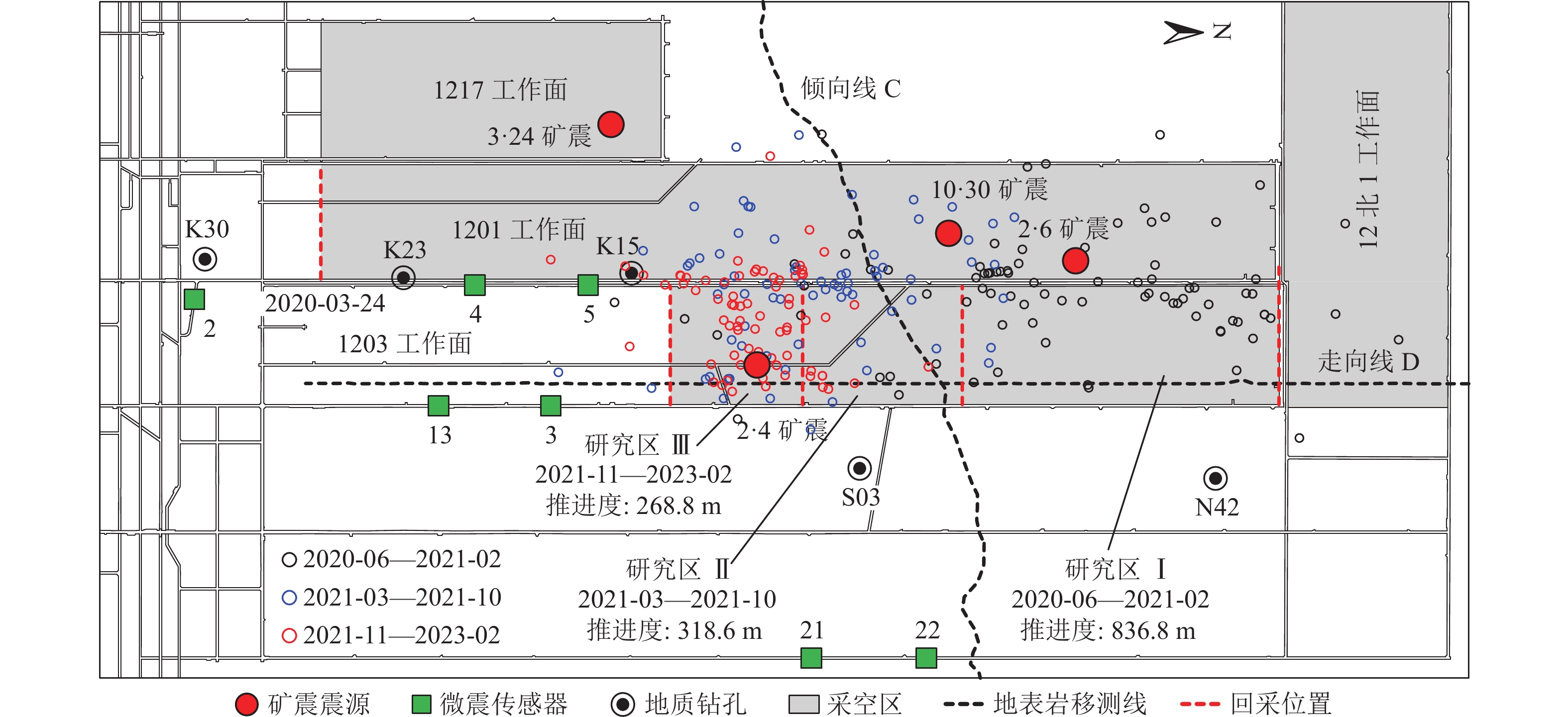
内蒙古自治区鄂尔多斯呼吉尔特矿区某深部矿井12盘区南北两翼布置，北翼综采开采2-2上煤层，煤层厚度4.39~5.85 m，平均4.92 m。主采1203工作面西邻1201、1217工作面采空区，工作面邻空回采期间已发生4起矿震事件，震源均位于采空区，其中3起为1203工作面回采期间发生，即“2·6”“10·30”和“2·4”矿震，3起矿震能量等级分别为4.78×106、4.15×105、8.94×106 J，工作面也因矿震问题强制停产93 d，矿震震源(>104 J)分布及其与工作面推进位置关系如图1所示。发生“2·6”矿震后，工作面复产期间矿震现象变得频繁。截至2023年12月31日，1203工作面已回采1 424.2 m，回采位置与1217工作面切眼平齐，后续工作面邻更大范围采空区回采，矿震风险进一步增大将再次制约矿井高效生产。
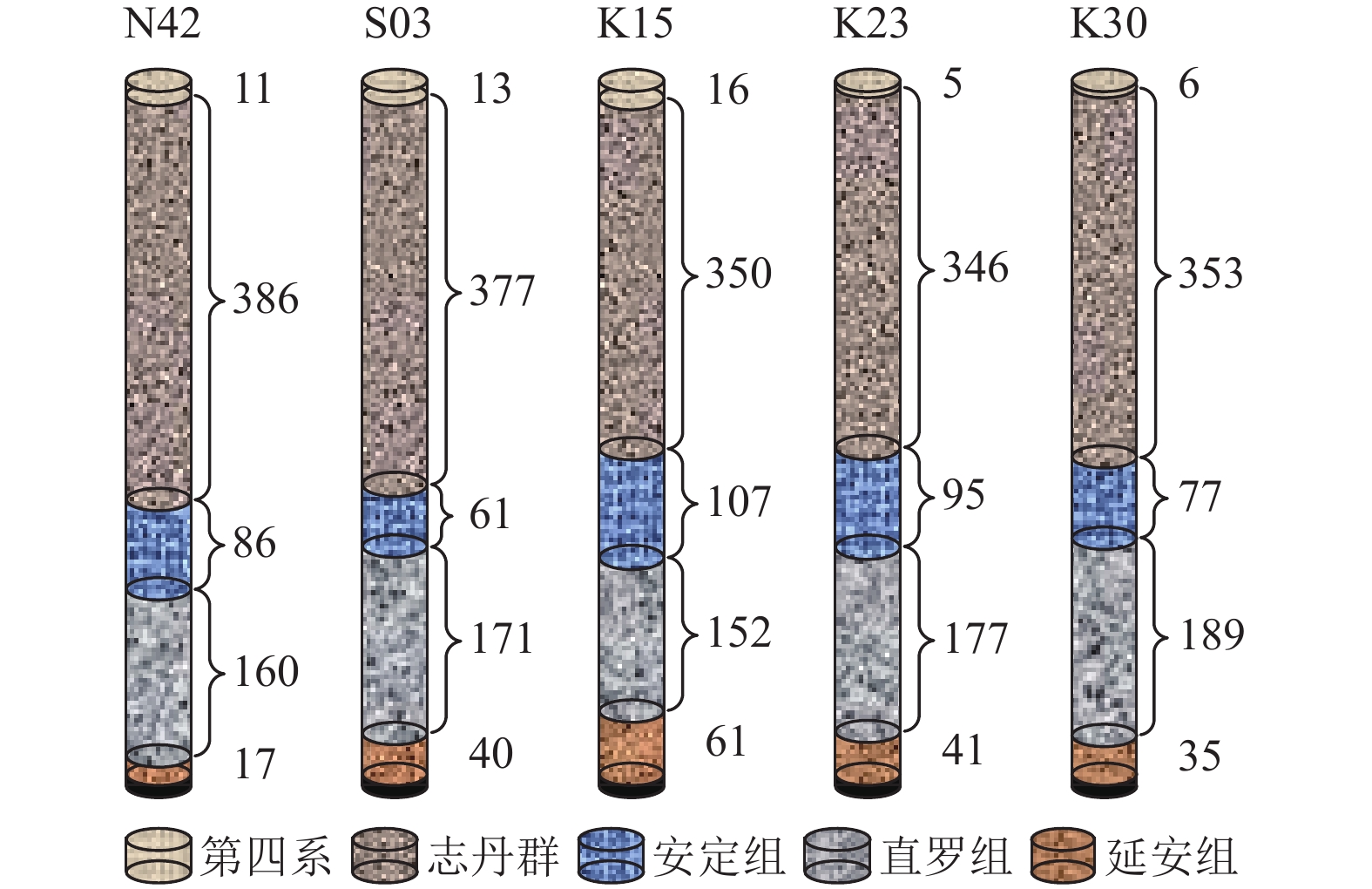
收集地质钻孔柱状信息，得到1203工作面沿走向煤层及其上覆地层分布特征，如图2所示，煤层上覆地层以第四系表土层厚度薄、白垩系志丹群整层厚度大为最典型特征，其中志丹群由厚层砂岩层构成，整层厚度达到350 m左右，因其整体性强、完整度高将整层岩层统称为巨厚覆岩。12盘区北翼地表布置了沿工作面走向、倾向岩层移动测点(图1)，以探究巨厚覆岩赋存地质环境岩层移动规律与矿震现象间联系。
![]()
图 2 沿工作面走向覆岩地层结构分布注：数字为岩层厚度，m。Figure 2. Stratigraphic structure distribution of the overburden along the strike of the No.1203 mining face1.2 震源分布与岩层移动规律
根据矿震发生情况将工作面划分为3个研究区域，统计研究区Ⅰ、Ⅱ、Ⅲ能级超过104 J的大能量微震事件共232起，平面分布如图1所示，微震分布呈逐渐向矿震震源处聚拢趋势，尤其对于研究区Ⅲ这一现象更为显著，表明触发矿震前存在覆岩逐层破断、诱发微震聚集的孕育过程。
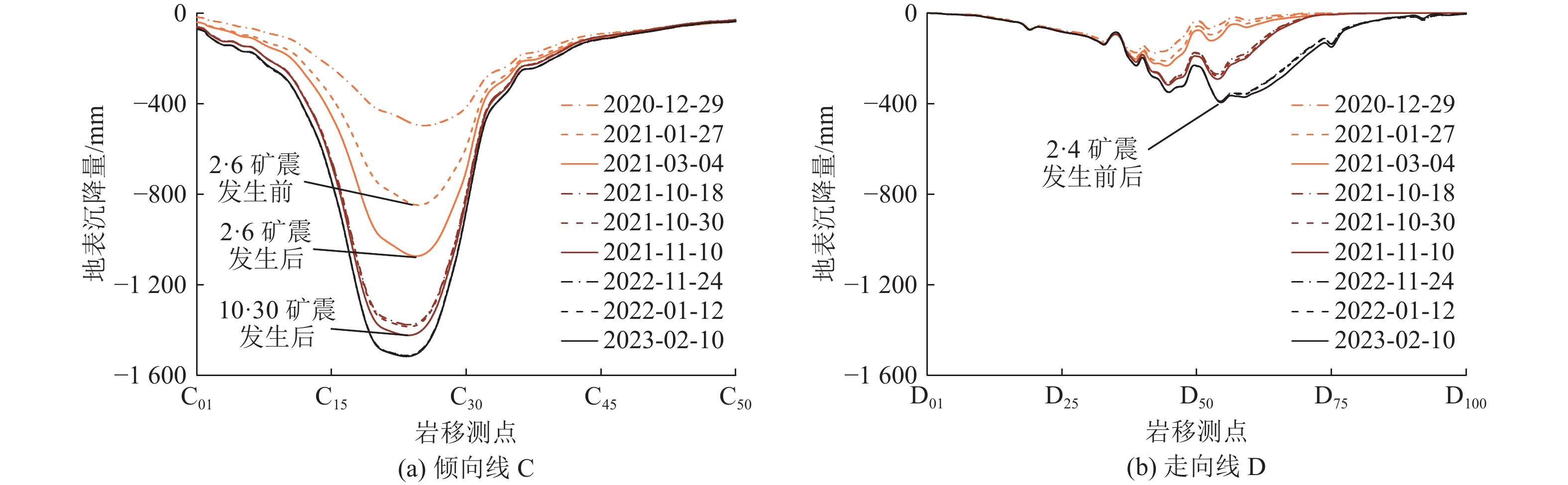
为揭示矿震孕育过程巨厚覆岩运移规律，定期开展地表岩层移动观测工作。统计筛选3起矿震事件发生前后观测数据，得到工作面开采期间沿倾向、走向岩层移动规律(图3)。如图3a所示，“2·6”矿震发生前地表最大沉降量由−494 mm迅速增大至−848 mm，弹性能快速积聚，矿震发生后，沉降量增大至−1 076 mm；“10·30”矿震发生后沉降量增加约−100 mm，巨厚覆岩处于失稳状态。结合图3b，“2·4”矿震发生前后地表最大沉降量基本不变，均为−397 mm，表明随工作面邻空开采范围增大，巨厚覆岩运移活动更易诱发矿震。
![]()
图 3 工作面不同回采阶段矿震发生前后地表岩层移动规律Figure 3. Movement patterns of surface rock layers before and after the mine earthquakes in different mining stages of the mining face当工作面接续推进过1217切眼后，邻空回采范围增大，巨厚覆岩可能发生更大尺度的联动破断运动，诱发矿震风险升高，解析巨厚覆岩矿震孕育破裂特征及触发过程的力学机制，对于揭示诱发矿震孕育规律，尤其从应力调控方面改变巨厚覆岩应力状态以达到降载减震目的。
2 巨厚覆岩结构破断演化规律
2.1 破断力学条件
根据岩层不同宽厚比划分为薄板、厚板两种类型[19]，对于本文工作面上覆巨厚覆岩分布特征，结合工作面开采条件可将其划分为厚板，分析不同回采条件下巨厚覆岩破断力学条件及其与矿震现象之间联系。
建立巨厚覆岩厚板力学模型，如图4a所示。1201工作面实体煤回采期间，倾向长度较小，采动裂隙未发育至巨厚覆岩层，此时巨厚覆岩边界条件为四边固支；随1203工作面回采，采场走向、倾向长度增大，巨厚覆岩长边和短边中点相继进入屈服状态，分别沿巨厚覆岩边界扩展形成塑性铰，边界条件由四边固支转变为四边简支[20](图4b)。
![]()
图 4 巨厚覆岩厚板力学模型及其边界条件Figure 4. Thick-plate mechanical model of the extremely-thick overburden and its boundary conditions根据符拉索夫厚板理论[21]，简支矩形厚板的平衡微分方程为：
$$ \left\{\begin{aligned} &\frac{D}{5}\left[ {\left( {1 - \mu } \right){\nabla ^2}{\psi _x} + \left( {1 + \mu } \right)\frac{{\partial \varphi }}{{\partial x}} + \frac{1}{2}\frac{{\partial ({\nabla ^2}w)}}{{\partial x}}} \right] +\\ &\qquad \frac{{Gh}}{3}\left(\frac{{\partial w}}{{\partial x}} - {\psi _x}\right) = 0 \\ & \frac{D}{5}\left[ {\left( {1 - \mu } \right){\nabla ^2}{\psi _y} + \left( {1 + \mu } \right)\frac{{\partial \varphi }}{{\partial y}} + \frac{1}{2}\frac{{\partial ({\nabla ^2}w)}}{{\partial y}}} \right] +\\ &\qquad \frac{{Gh}}{3}\left(\frac{{\partial w}}{{\partial y}} - {\psi _y}\right) = 0 \\ & \frac{2}{3}Gh\left[ {{\nabla ^2}w - \varphi } \right] + q(x,y) = 0\end{aligned}\right. $$ (1) 其中，
$ D=\dfrac{E{H}^{2}}{12(1-{\mu }^{2})} $ ；$ \varphi = \dfrac{{\partial {\psi _x}}}{{\partial x}} + \dfrac{{\partial {\psi _y}}}{{\partial y}} $ ；$ G=\dfrac{E}{2(1+\mu )} $ 。考虑厚板边界扭转剪切变形效应，巨厚覆岩破坏前的简支边界条件可表示为：
$$ \left\{\begin{aligned} &x=\pm \frac{a}{2}时：w=0,{\psi }_{y}=0,{M}_{x}=0\\ &y=\pm \frac{b}{2}时：w=0,{\psi }_{x}=0,{M}_{y}=0\end{aligned}\right. $$ (2) 将挠度、转角的位移函数和载荷展开成双三角级数形式：
$$ \left\{ \begin{gathered} w = \sum\nolimits_{m = 1}^\infty {\sum\nolimits_{n = 1}^\infty {\left[ {\frac{{{a^2}{b^2}}}{{4D{\pi ^4}({m^2}{b^2} + {n^2}{a^2})}} + \frac{6}{{5GH{\pi ^2}}}} \right]A} } \\ {\psi _x} = \sum\nolimits_{m = 1}^\infty {\sum\nolimits_{n = 1}^\infty {\left[ {\frac{{ma{b^2}}}{{2D{\pi ^3}({m^2}{b^2} + {n^2}{a^2})}} - \frac{{3m}}{{5a\pi GH}}} \right]B} } \\ {\psi _y} = \sum\nolimits_{m = 1}^\infty {\sum\nolimits_{n = 1}^\infty {\left[ {\frac{{n{a^2}{b^2}}}{{2aD{\pi ^3}({m^2}{b^2} + {n^2}{a^2})}} - \frac{{3n}}{{5a\pi GH}}} \right]A} } \\ q = \sum\nolimits_{m = 1}^\infty {\sum\nolimits_{n = 1}^\infty {{q_{mn}}\sin \frac{{2m\pi x}}{a}\sin \frac{{2n\pi y}}{b}} } \\ \end{gathered} \right. $$ (3) 上式中：
$$ \left\{ \begin{gathered} A = {q_{mn}}\sin \frac{{2m\pi x}}{a}\sin \frac{{2n\pi y}}{b} \\ B = {q_{mn}}\cos \frac{{2m\pi x}}{a}\sin \frac{{2n\pi y}}{b} \\ \end{gathered} \right. $$ (4) 在保证计算精度情况下，为简化计算取m=n=1，联立式(1)、式(3)得到厚板中力矩表达式：
$$ \left\{ \begin{gathered} {M_x} = \dfrac{{{q_{11}}}}{5}\left[ {\dfrac{{5{b^2} + 4\mu ab + \mu {a^2}}}{{4{\pi ^2}{{\left(\dfrac{b}{a} + \dfrac{a}{b}\right)}^2}}} + \dfrac{{6D\mu ({a^2} - ab)}}{{5GH({b^2} + {a^2})}}} \right]C \\ {M_y} = \dfrac{{{q_{11}}}}{5}\left[ {\dfrac{{5{b^2} + 4\mu ab + \mu {a^2}}}{{4{\pi ^2}{{\left(\dfrac{b}{a} + \dfrac{a}{b}\right)}^2}}} + \dfrac{{6D\mu ({b^2} - ab)}}{{5GH({b^2} + {a^2})}}} \right]C \\ \end{gathered} \right. $$ (5) 其中：
$$ \left\{ \begin{gathered} C = \sin \frac{{2\pi x}}{a}\sin \frac{{2\pi y}}{b} \\ q = \rho gh \\ \end{gathered} \right. $$ (6) $ {M_x} $ 、$ {M_y} $ 分别在x=a/4、y=b/4处取得最大值，令$ {M_x} $ =$ {M_y} $ ，得到厚板最大拉应力σt, max在其下表面取得[22]：$$ \begin{aligned} &{\sigma _{{\mathrm{t}},\max }} = \dfrac{{12{M_{\max }}}}{{{H^3}}}{\textit{z}} = \dfrac{{12{M_{\max }}}}{{{H^3}}} \cdot \dfrac{H}{2} = \\ &\qquad \dfrac{{3q(5{b^2} + 4\mu ab + \mu {a^2})}}{{10{\pi ^2}{{\left(\dfrac{b}{a} + \dfrac{a}{b}\right)}^2}{H^2}}} + \dfrac{{6q\mu ({a^2} - ab)}}{{25(1 - \mu )({b^2} + {a^2})}} \end{aligned}$$ (7) 将巨厚覆岩不同层位拉应力极限作为其破坏判据，根据图2，巨厚覆岩上覆岩层自重应力约为0.25 MPa；巨厚覆岩的泊松比取0.22；抗拉强度约为2.62 MPa；厚度约为350 m；巨厚覆岩走向、倾向跨度可表示为：a(b)=L−2H1/tanβ，约为300 m，β为岩层移动角，取70°。
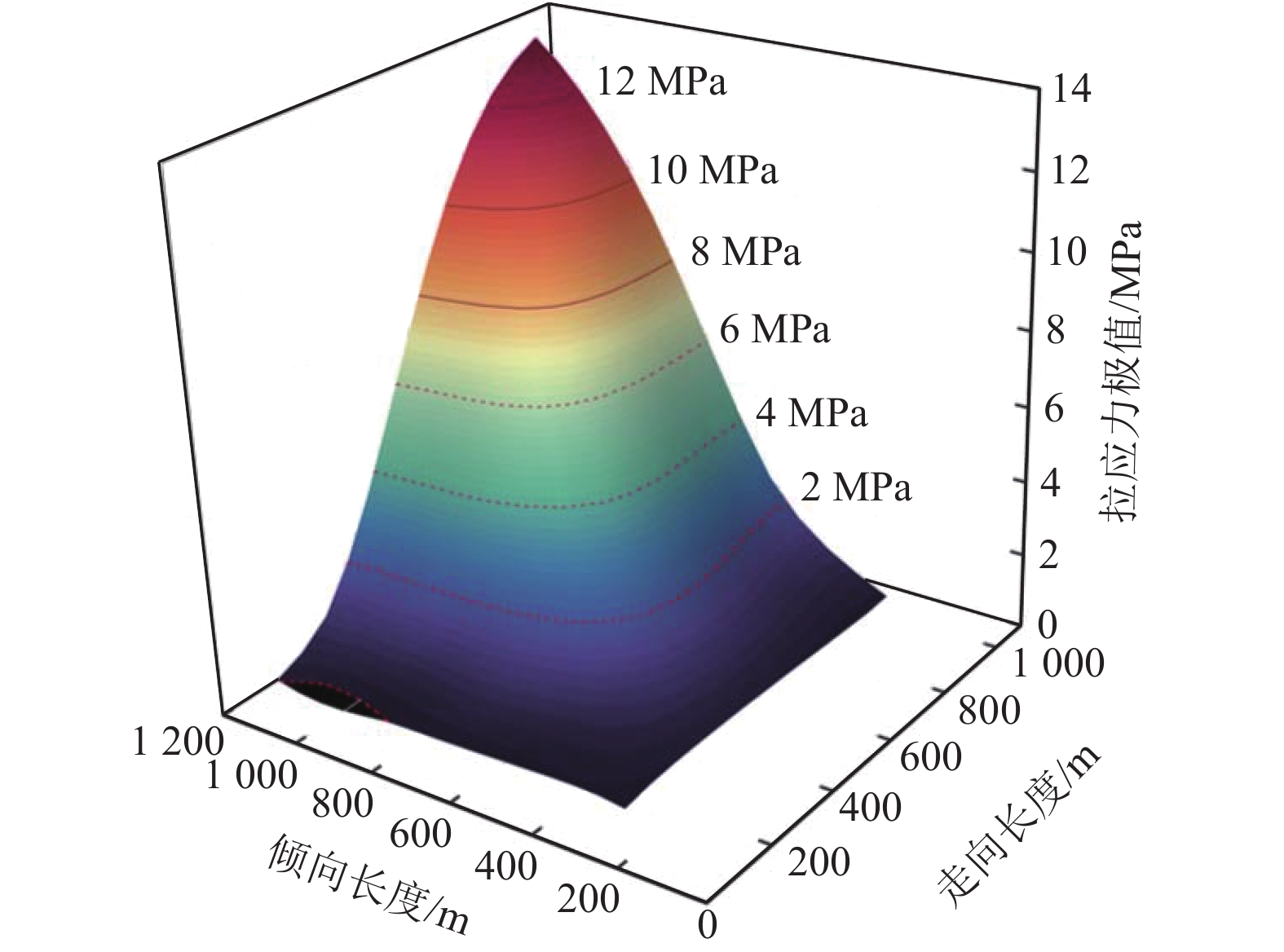
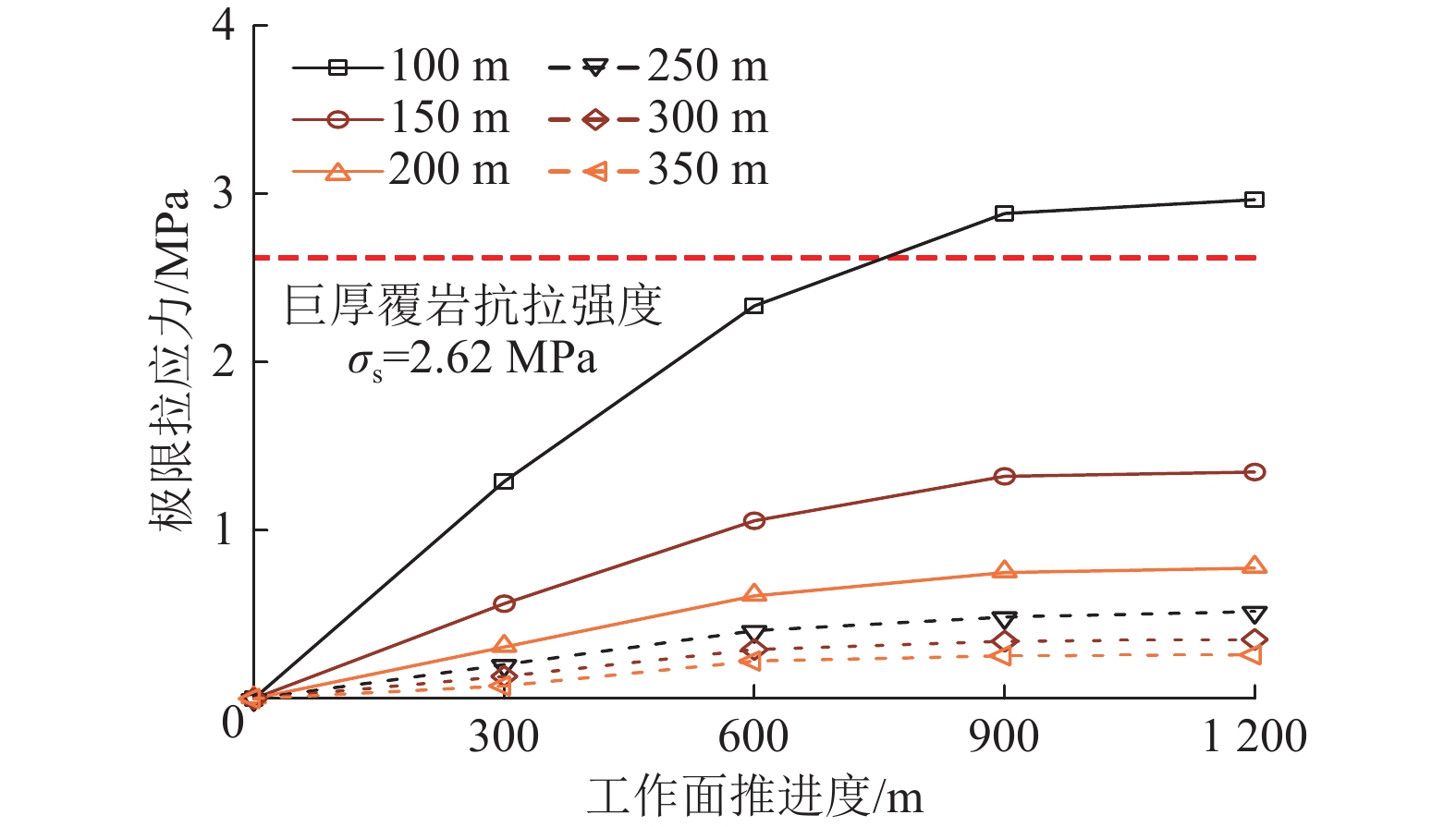
综上，得到工作面不同采空条件下巨厚覆岩下部拉应力极值分布情况，如图5所示。显然，工作面邻空回采导致巨厚覆岩走向、倾向跨度增大，其下部拉应力随之增加，从而导致其稳定性降低。巨厚覆岩拉应力极限受其短边跨度影响最大，单一工作面回采时，采空范围并未达到巨厚覆岩破断倾向宽度条件，因此巨厚覆岩拉应力极值并未达到其抗拉强度；当1203工作面回采时，倾向长度为600 m，走向推进长度达到800 m后，巨厚覆岩拉应力极值为2.62 MPa，超过其抗拉强度，巨厚覆岩破断。
![]()
图 5 不同采空条件巨厚覆岩拉应力极值分布Figure 5. Distribution of the extrema of tensile stresses in the significantly thick overburden under different goaf conditions结合图1中工作面推进情况，2021年2月6日1203工作面邻空推进进尺达到836.8 m时，发生“2·6”矿震，“10·30”“2·4”矿震则为巨厚覆岩周期破断诱发[23]。因此认为，巨厚覆岩的初次破断步距约为800 m，巨厚覆岩破断是诱发矿震的主要原因。
2.2 破断演化特征
进一步分析工作面后续回采过程中不同开采条件对巨厚覆岩破断的影响。
如图6所示，随着1203工作面推进长度增加，巨厚覆岩不同层位拉应力极值增长幅度逐渐变缓。采空区倾向长度为600 m时，随着推进长度增加，巨厚覆岩并未整层发生破断，而仅有其下部100 m厚度范围发生破断。对于巨厚覆岩下部厚度超过100 m的层位，拉应力极值整体低于巨厚覆岩抗拉强度，且处于较小的范围内。
![]()
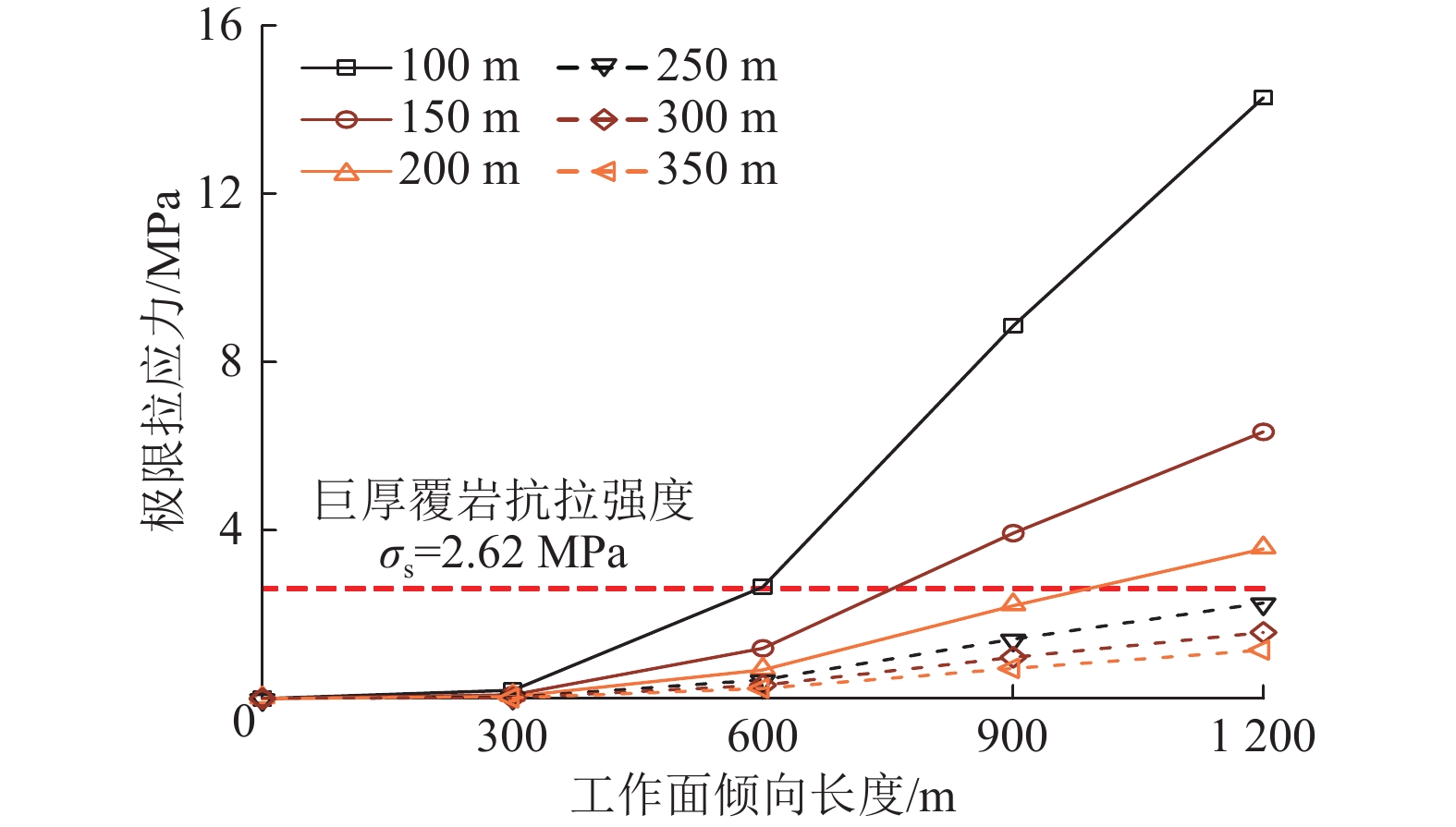
图 6 巨厚覆岩下部不同破断层位拉应力随工作面推进度变化关系Figure 6. Tensile stresses of different fractured layers in the lower part of the significantly thick overburden varying with the advancement of the No.1203 mining face对于图7，倾向长度增大对于巨厚覆岩不同层位拉应力极值有较大影响，倾向长度超过600 m后，巨厚覆岩下部100 m岩层拉应力极值增幅最为明显，而对于巨厚覆岩下部150 m岩层，当采空区倾向长度达到900 m时，岩层拉应力极值达到了3.94 MPa，已超过巨厚覆岩抗拉强度(2.62 MPa)，后续1203工作面继续推进，邻空范围更大，巨厚覆岩破断尺度更大，将面临更大的矿震风险，巨厚覆岩破断运移为矿震形成触发的动力和能量来源。
![]()
图 7 巨厚覆岩下部不同破断层位拉应力随工作面倾向长度的变化关系Figure 7. Tensile stresses of different fractured horizons in the lower portion of the significantly thick overburden varying with the inclination length of the No.1203 mining face3 基于震源机制解析的应力反演方法
3.1 波形预处理及震源机制解析
3.1.1 矿震波形主成分预处理
矿震作为因矿山活动引起的非天然地震现象[24]，其波形因采矿地质环境干扰，使得震源破裂机制解析难度增大、准确率降低。采用主成分分析方法预处理波形[25]，提高波形信噪比，为后续震源机制求解提供高质量数据。
将i个传感器收集到的微震事件震动信号构建k阶数据矩阵X，得到波形主成分矩阵XPCA：
$$ \boldsymbol{X} _{ \mathrm{PCA}} \mathit= \boldsymbol{XW} $$ (8) 式中，k阶矩阵W表示波形主成分权重，由协方差矩阵XTX特征向量构成。
基于上式，微震波形第一主成分XPCA(1)及其波形权重W(i)可表示为：
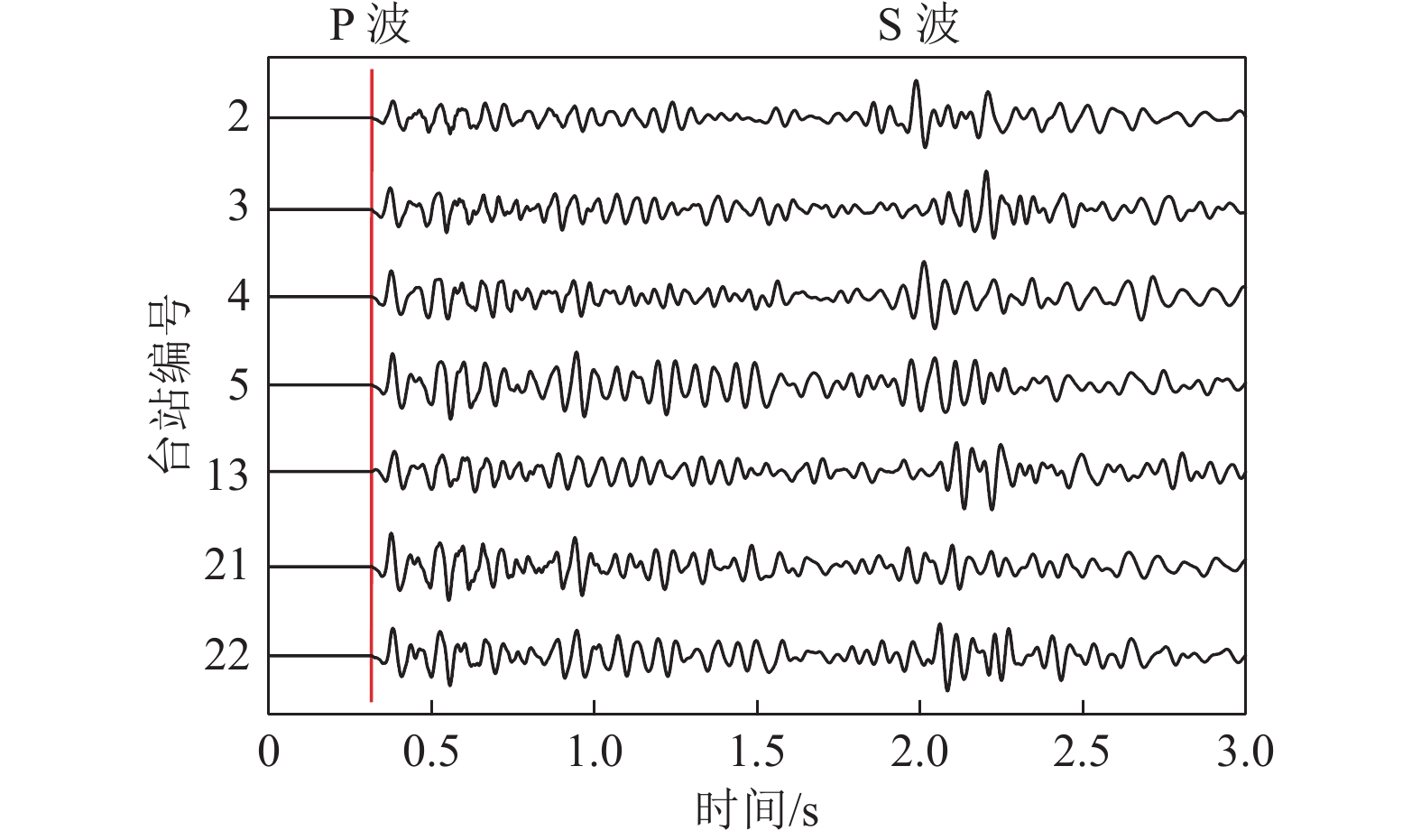
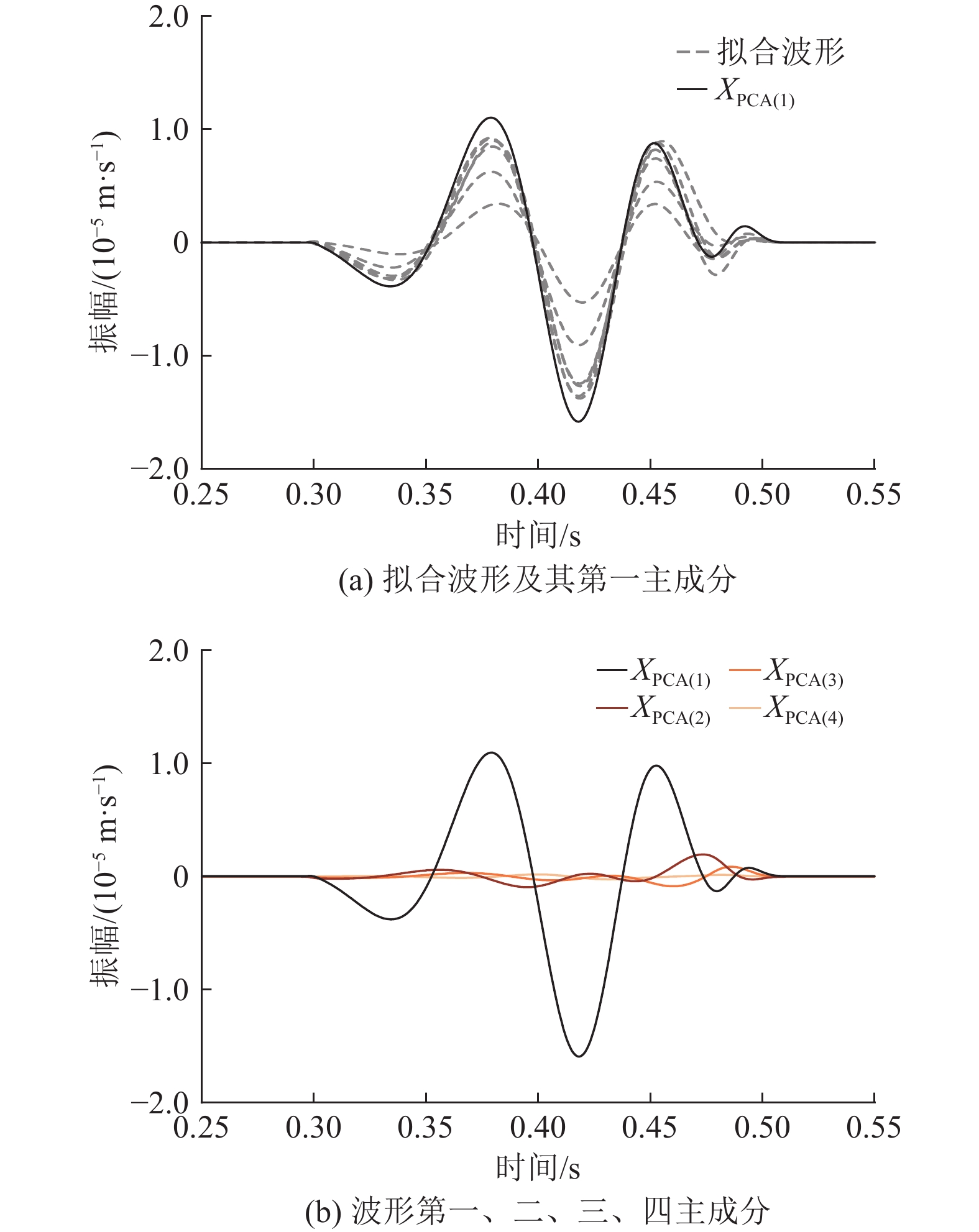
$$ \boldsymbol{X} _{ \mathit{i} } \mathrm= \boldsymbol{X} _{ \mathrm{PCA(1)}} \boldsymbol{W} _{ \mathrm{(} \mathit{i} \mathrm{)}}^{ \mathrm{T}} $$ (9) 根据微震传感器布置情况(图1)，对微震事件震动波形带通滤波(5~10 Hz)(图8)用于后续主成分提取，图9为一微震拟合波形及其第一、二、三、四主成分。在获取波形主成分和有效位移振幅后可进一步求解震源矩张量。
![]()
图 9 微震波形主成分分析Figure 9. Principal component analysis results of microseismic waveforms3.1.2 矩张量反演及破裂信息求解
矩张量反演已成为分析矿震震源破裂机制的有效方法[26]，在获取波形主成分后，借助有效位移振幅与格林函数间联系可求解矩张量[27]：
$$\left\{\begin{aligned} &{\boldsymbol{M}}_{{\mathrm{s,r}}}={\boldsymbol{u}}(x_{\mathrm{r}},t_{\mathrm{r}})/G_{{\mathrm{s,r}}}\\ &{\boldsymbol{u}}\left( {{x_{\mathrm{r}}},{t_{\mathrm{r}}}} \right) = \iiint\limits_V {\left[ {G\left( {{x_{\mathrm{r}}},{x_{\mathrm{s}}}} \right) \times f\left( {{x_{\mathrm{s}}}} \right)} \right]{{\mathrm{d}}^3}{x_{\mathrm{s}}}} \end{aligned} \right.$$ (10) 获取矩张量Ms,r后，本征值化得到特征值λ1、λ2、λ3(λ1≥λ2≥λ3)，将其分解为CISO(矩张量各向同性成分)、CCLVD(矩张量轴向拉伸成分)及CDC(矩张量剪切破裂成分)分量，进而可计算震源破裂各向同性、轴向拉伸及剪切成分的占比情况PISO、PCLVD、PDC[28]。
$$ \left\{ \begin{gathered} {C_{{\mathrm{ISO}}}} = \frac{1}{3}\left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right) \\ {C_{{\mathrm{CLVD}}}} = \frac{2}{3}\left( {{\lambda _1} + {\lambda _3} - 2{\lambda _2}} \right) \\ {C_{{\mathrm{DC}}}} = \frac{1}{2}\left( {{\lambda _1} - {\lambda _3} - \left| {{\lambda _1} + {\lambda _3} - 2{\lambda _2}} \right|} \right) \\ \end{gathered} \right. $$ (11) $$ \left\{ \begin{gathered} {P_{{\mathrm{ISO}}}} = \frac{{{C_{{\mathrm{ISO}}}}}}{{{C_{{\mathrm{ISO}}}} + {C_{{\mathrm{CLVD}}}} + {C_{{\mathrm{DC}}}}}} \times 100\text{%} \\ {P_{{\mathrm{CLVD}}}} = \frac{{{C_{{\mathrm{CLVD}}}}}}{{{C_{{\mathrm{ISO}}}} + {C_{{\mathrm{CLVD}}}} + {C_{{\mathrm{DC}}}}}} \times 100\text{%} \\ {P_{{\mathrm{DC}}}} = \frac{{{C_{{\mathrm{DC}}}}}}{{{C_{{\mathrm{ISO}}}} + {C_{{\mathrm{CLVD}}}} + {C_{{\mathrm{DC}}}}}} \times 100\text{%} \\ \end{gathered} \right. $$ (12) 根据矩张量Ms,r的特征值λ1、λ2、λ3及(λ1、λ3)对应特征向量(e1、e3)，通过式(6)求解震源破裂面法向向量n和滑移向量v，可进一步获取震源破裂面产状信息[29]，用于应力场反演。
$$ \left\{ \begin{gathered} {\boldsymbol{n}} = \sqrt {\frac{{{\lambda _1} - {\lambda _2}}}{{{\lambda _1} - {\lambda _3}}}} {{\boldsymbol{e}}_1} + \sqrt {\frac{{{\lambda _1} - {\lambda _2}}}{{{\lambda _1} - {\lambda _3}}}} {{\boldsymbol{e}}_3} \\ {\boldsymbol{v}} = \sqrt {\frac{{{\lambda _1} - {\lambda _2}}}{{{\lambda _1} - {\lambda _3}}}} {{\boldsymbol{e}}_1} - \sqrt {\frac{{{\lambda _1} - {\lambda _2}}}{{{\lambda _1} - {\lambda _3}}}} {{\boldsymbol{e}}_3} \\ \end{gathered} \right. $$ (13) 3.2 矿震震源应力反演方法改进
准确获取震源破裂信息是保证应力场反演精度的基础，而应力反演力学模型则起到决定性作用。传统应力反演方法主要基于BOTT提出的剪切力学模型[30]，假设σij为破裂面应力张量，则破裂面有效牵引应力Ti为：
$$ {{\boldsymbol{T}}_i} = {{\boldsymbol{\sigma}} _{ij}}{n_j} $$ (14) 有效牵引应力T沿破裂面方向、切向的应力分量σn、τi可表示为：
$$ \left\{ \begin{gathered} {\sigma _{\mathrm{n}}} = {{\boldsymbol{T}}_i}{n_i} = {{\boldsymbol{\sigma}} _{ij}}{n_i}{n_j} \\ {\tau _{\mathrm{i}}} = {{\boldsymbol{T}}_i} - {\sigma _{\mathrm{n}}}{n_i} = {\sigma _{kj}}{n_k}\left( {{\delta _{ik}} - {n_i}{n_k}} \right) \\ \end{gathered} \right. $$ (15) 归一化切向应力可进一步确定绝对应力值，从而将震源应力反演方程转换为：
$$ {\boldsymbol{V}} = {\sigma _{kj}}{n_j}\left( {{\delta _{ik}} - {n_i}{n_k}} \right) $$ (16) 上式以矩阵形式表示为：
$$ {\boldsymbol{V}} = {\boldsymbol{A\sigma}} $$ (17) 式中，应力张量σ=[σ11 σ22 σ33 σ23 σ13 σ12]；A是由震源破裂面法向向量n组成的3×6阶矩阵，矩阵A表示为：
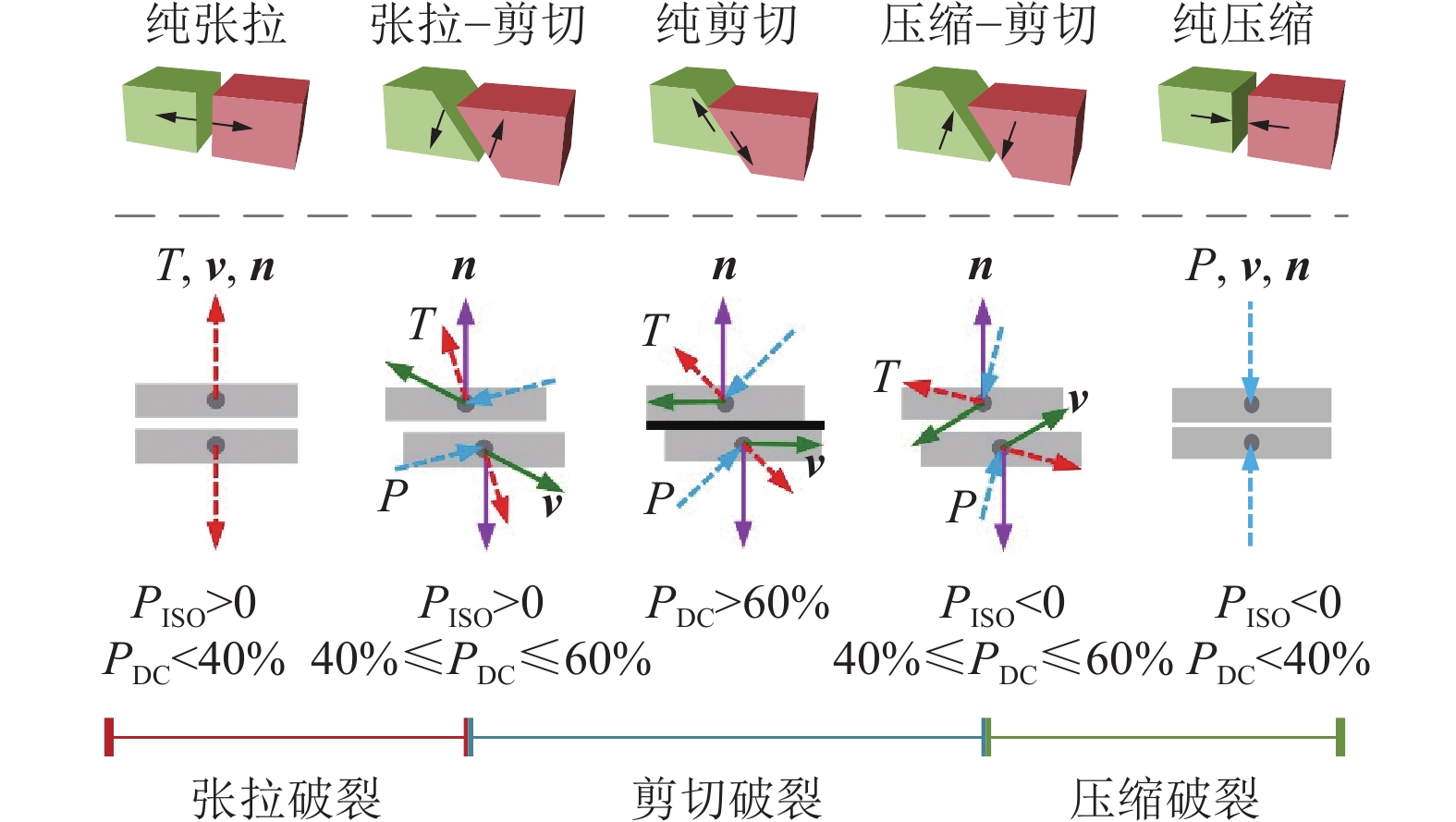
$$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{n_1}\left( {1 - {n_1}^2} \right)}&{ - {n_1}{n_2}^2}&{ - {n_1}{n_3}^2}&{ - 2{n_1}{n_2}{n_3}}&{{n_3}\left( {1 - 2{n_1}^2} \right)}&{{n_2}\left( {1 - 2{n_1}^2} \right)} \\ { - {n_2}{n_1}^2}&{{n_2}\left( {1 - {n_2}^2} \right)}&{ - {n_2}{n_3}^2}&{{n_3}\left( {1 - 2{n_2}^2} \right)}&{ - 2{n_1}{n_2}{n_3}}&{{n_1}\left( {1 - 2{n_2}^2} \right)} \\ { - {n_3}{n_1}^2}&{ - {n_3}{n_2}^2}&{{n_3}\left( {1 - {n_3}^2} \right)}&{{n_2}\left( {1 - 2{n_3}^2} \right)}&{{n_1}\left( {1 - 2{n_3}^2} \right)}&{ - 2{n_1}{n_2}{n_3}} \end{array}} \right] $$ (18) 但对于煤矿开采地质环境，诱发震源破裂类型除纯剪切破裂外，根据矩张量各向同性、轴向拉伸分量占比不同，还存在如图10所示的典型张拉、压缩破裂类型震源[31]。
![]()
图 10 震源破裂类型判识准则Figure 10. Criteria for discriminating the fracture types of seismic sources因此，按文献[32]提出的修正力学模型：假设有效牵引力不再分解，即有效牵引方向与矩张量解析得到的破裂面滑移矢量v方向平行，因此对于张拉、压缩等非纯剪切破裂机制震源，其滑移向量并不平行于破裂面。基于该假设，式(14)可转化为：
$$ {{\boldsymbol{T}}} _{ \mathit{i} }^{ \mathrm{e}} \mathrm= {{\boldsymbol{\sigma}} } _{ \mathit{ij} }^{ \mathrm{e}} \mathit{n} _{ \mathit{j} } \mathrm{=(} {{\boldsymbol{\sigma}} } _{ \mathit{ij} } \mathrm- \mathit{\delta } _{ \mathit{ij} } \mathit{F} \mathrm{)} \mathit{n} _{ \mathit{j} } $$ (19) 式(19)的矩阵表现形式为：
$$ \boldsymbol{V} \mathrm= \boldsymbol{A\sigma } ^{ \mathrm{e}} $$ (20) 式中，破裂面法向向量组成的矩阵A简化表示为：
$$ {\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{n_1}}&0&0&0&{{n_3}}&{{n_2}} \\ 0&{{n_2}}&0&{{n_3}}&0&{{n_1}} \\ 0&0&{{n_3}}&{{n_2}}&{{n_1}}&0 \end{array}} \right] $$ (21) 应力反演可求解主应力作用方位，但并不能求解绝对的应力张量值，而是通过应力形因子R反映主应力σ1、σ2、σ3的相对大小及应力场分布状态[33]。本文基于上述修正应力反演力学模型(式19)，改进Vavrycuk提出的反演算法[34]，用于后续非纯剪切破裂震源的应力场反演。
4 巨厚覆岩矿震孕育破裂特征与应力场演化
4.1 矿震孕育过程覆岩断裂特征
基于矩张量反演方法求解研究区Ⅰ、Ⅱ、Ⅲ矿震发生前微震震源矩张量，如图11所示，采用CLVD-ISO钻石图统计分析震源孕育破裂特征[35]。图11a中，“2·6”矿震发生前，震源破裂模式主要表现为张拉、压缩、剪切破裂，即工作面邻空开采期间，采空区影响下顶板逐层破断，岩层失稳错动诱发大能量震动事件；图11b表明，“2·6”矿震发生后，工作面停产58 d后复产使得顶板结构转变为失稳状态，随工作面继续推进，岩层运动主要以张拉破断形式呈现，较“2·6”矿震而言，“10·30”矿震孕育触发过程中岩层活动性更强；当工作面向更大范围采空区推进时，微震事件主要在1203工作面后方采空区聚集，图11c结果显示工作面岩层破断诱发震源破裂类型主要以压缩破裂为主，伴随少量纯张拉震源，如“2·4”矿震。工作面受到侧向更大范围采空区影响，巨厚覆岩大尺度联动破断可能诱发更高能级的矿震事件。
![]()
图 11 不同回采阶段震源类型CLVD−ISO钻石图Figure 11. CLVD-ISO diamond diagrams showing the fracturing types of seismic sources in different mining stages得到3起矿震震源矩张量后，采用Focalmech程序[36]绘制沙滩球，结合图10判别3起矿震震源均为纯张拉破裂，汇总结果如图12所示，其中“2·6”“10·30”“2·4”矿震轴向拉伸成分占主导，分别为65.72%、63.07%和65.93%，表明侧向采空区与后方采空区协同影响下，诱发矿震的巨厚覆岩孕育断裂特征均表现为张拉破断，巨厚覆岩断裂过程则与应力场作用方式密切相关。
4.2 矿震震源应力场演化规律
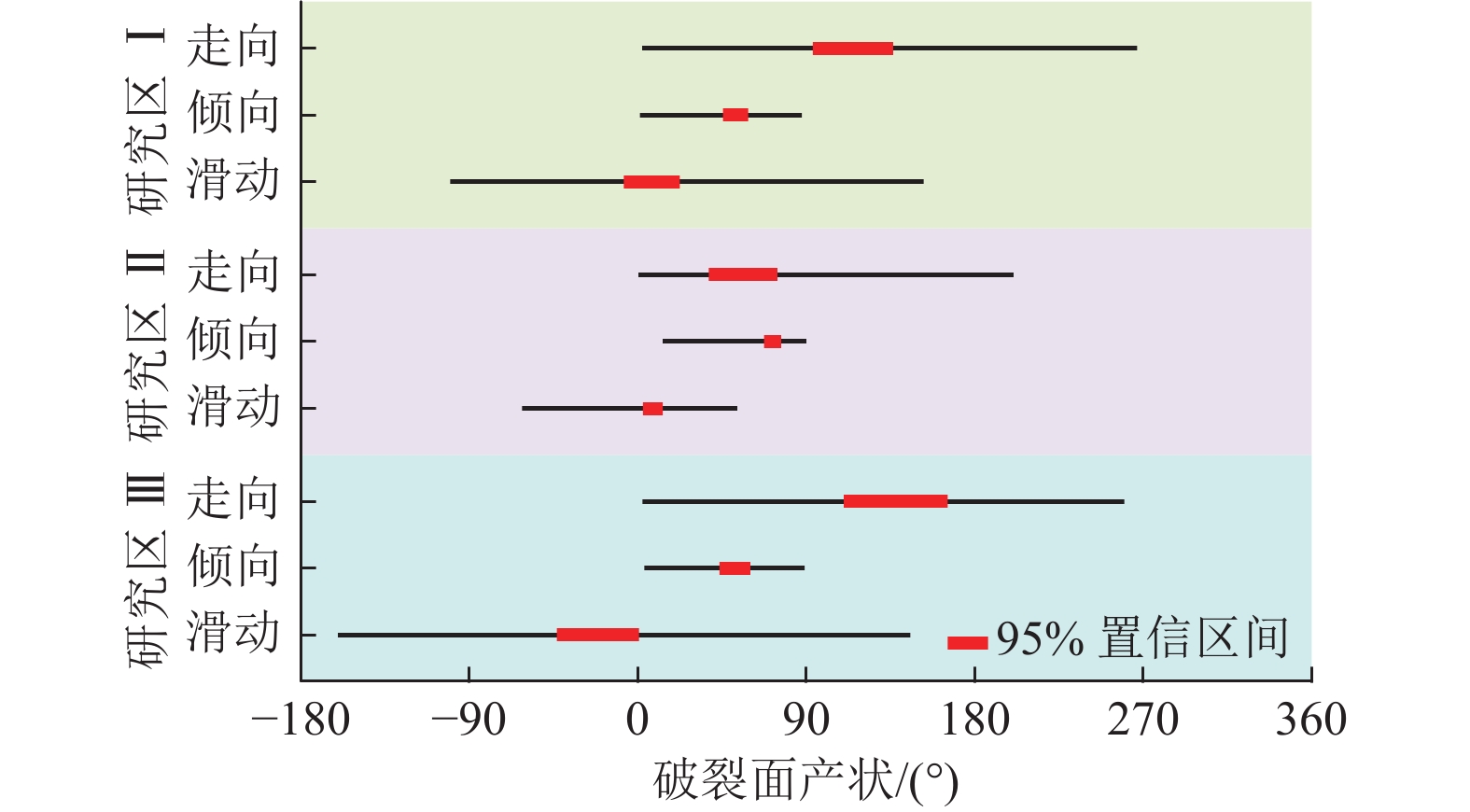
统计微震震源破裂面产状信息(图13)，研究区Ⅰ、Ⅱ、Ⅲ破裂面走向、倾向及滑动方位分布范围较为集中，将研究区Ⅰ、Ⅱ、Ⅲ各类破裂震源破裂面产状(95%置信区间)输入相应的应力反演模型，通过数值运算即可得到主应力方位及其相对大小关系。
![]()
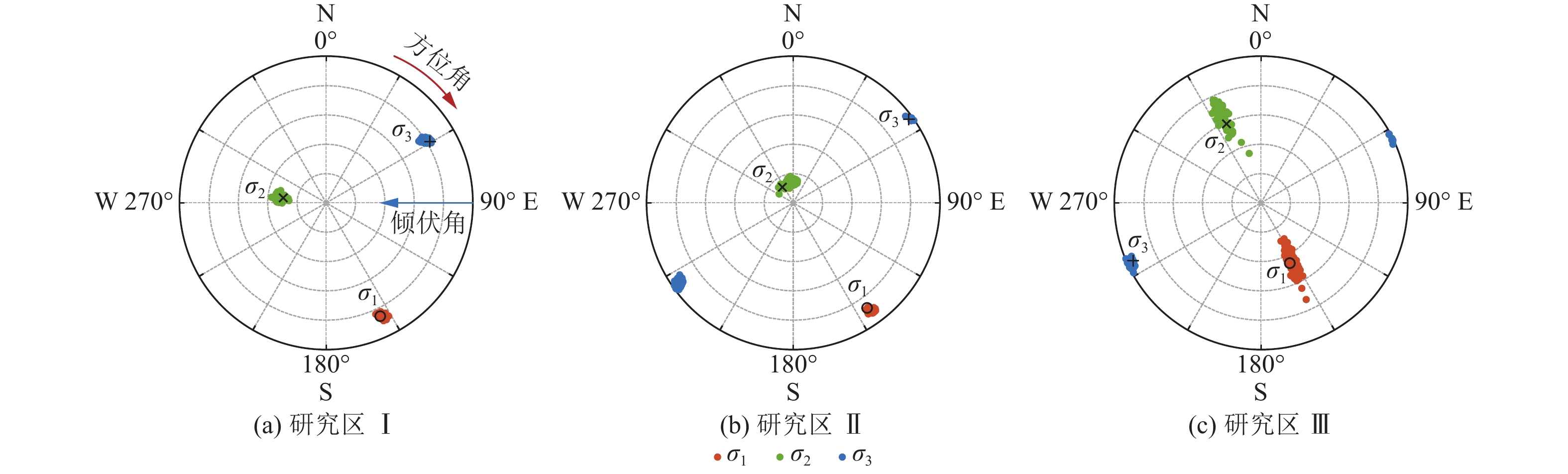
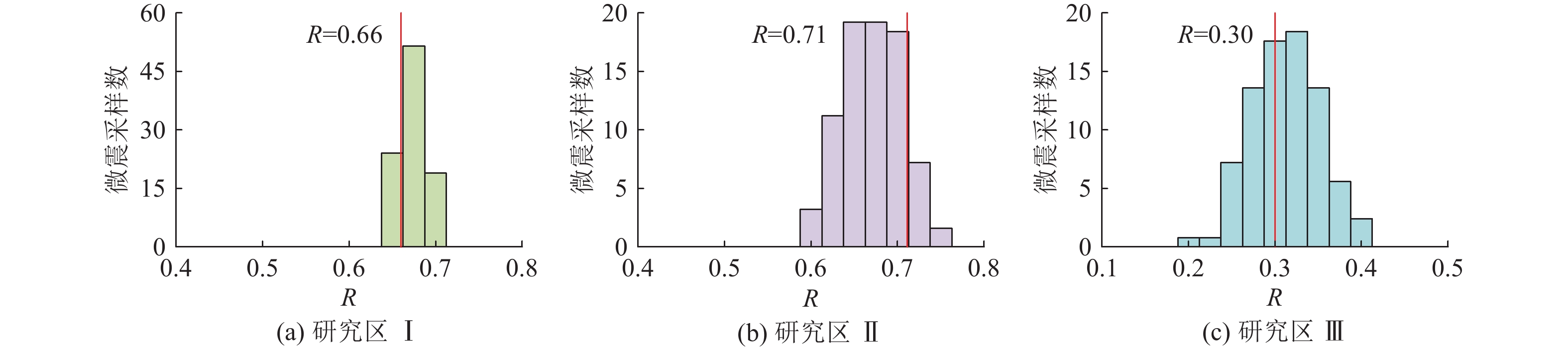
图 13 研究区Ⅰ、Ⅱ、Ⅲ震源破裂面产状信息Figure 13. Information on the occurrence of fracture planes of seismic sources in study areas Ⅰ, Ⅱ, and Ⅲ根据震源破裂面信息，应力反演结果见表1、如图14所示。研究区Ⅰ、Ⅱ、Ⅲ最大主应力σ1作用方位基本一致，侧向采空范围增大后，倾伏方向由近似水平转变为倾斜约53.79°；最小主应力σ3作用方位变化不大，随工作面推进应力作用倾伏方向逐渐转变为水平。结合应力形因子R分布情况(图15)，对于研究区Ⅰ、Ⅱ，R分别为0.66、0.71，整体应力分布以最大主应力为主导，呈现为单轴挤压应力状态，“2·6”“10·30”矿震应力作用机制相似；研究区Ⅲ的R为0.30，主要因最大主应力倾伏方向变化改变了整体应力分布状态，最小主应力相对增大，在最大主应力和最小主应力双轴挤压作用下，巨厚覆岩发生更大尺度联动破断，从而诱发了“2·4”矿震。
表 1 工作面不同回采阶段主应力分布情况Table 1. Distributions of principal stresses in different mining stages of the No.1203 mining face主应力 方位角α/(°)；倾伏角θ/(°) 研究区Ⅰ 研究区Ⅱ 研究区Ⅲ σ1 153.83；12.98 143.96；10.48 151.72；53.79 σ2 275.42；66.24 284.66；76.56 335.94；36.13 σ3 59.14；19.54 52.41；8.32 244.47；2.01 ![]()
图 14 研究区Ⅰ、Ⅱ、Ⅲ应力场分布情况Figure 14. Distributions of stress fields in study areas Ⅰ, Ⅱ, and Ⅲ![]()
图 15 研究区Ⅰ、Ⅱ、Ⅲ应力形因子分布情况Figure 15. Distributions of stress shape factors in study areas Ⅰ, Ⅱ, and Ⅲ5 巨厚覆岩矿震应力触发机制
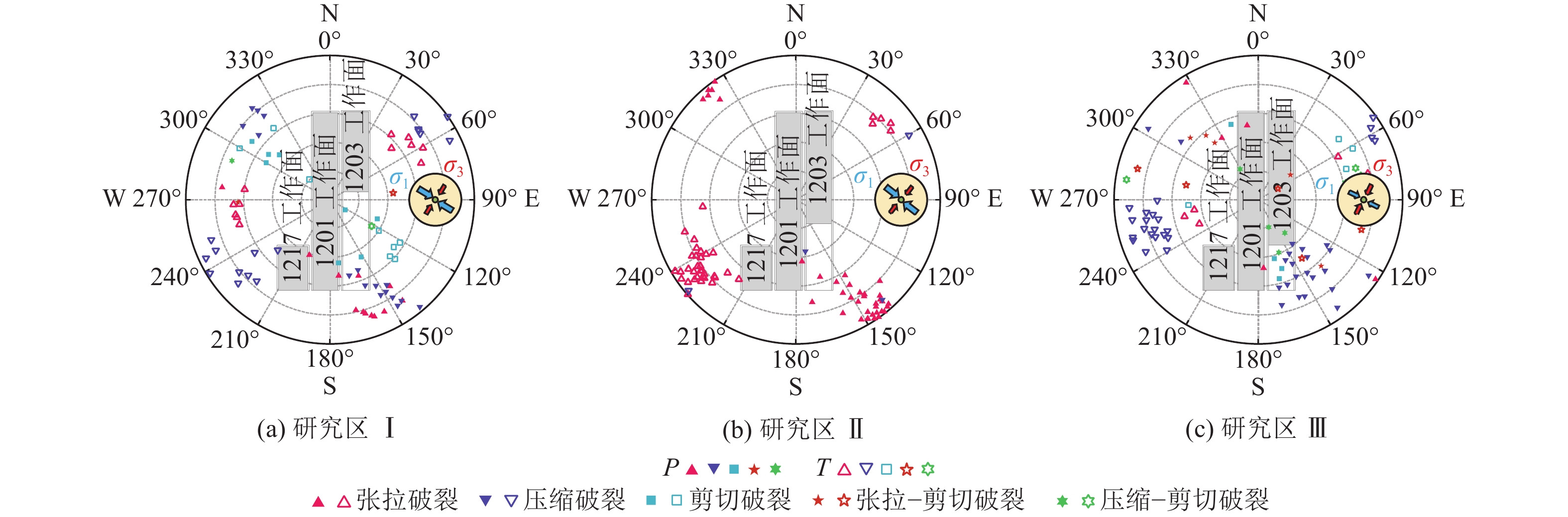
为进一步分析主应力对矿震的触发机制，按震源破裂类型求解各研究区微震震源破裂面P、T轴分布及其与工作面相对位置关系，如图16所示。P、T轴分布方位分别对应最大、最小主应力分布方位，各研究区P轴方位在125°~175°、300°~330°区间集中性较好，T轴方位在45°~90°、210°~270°区间集中性较好。
![]()
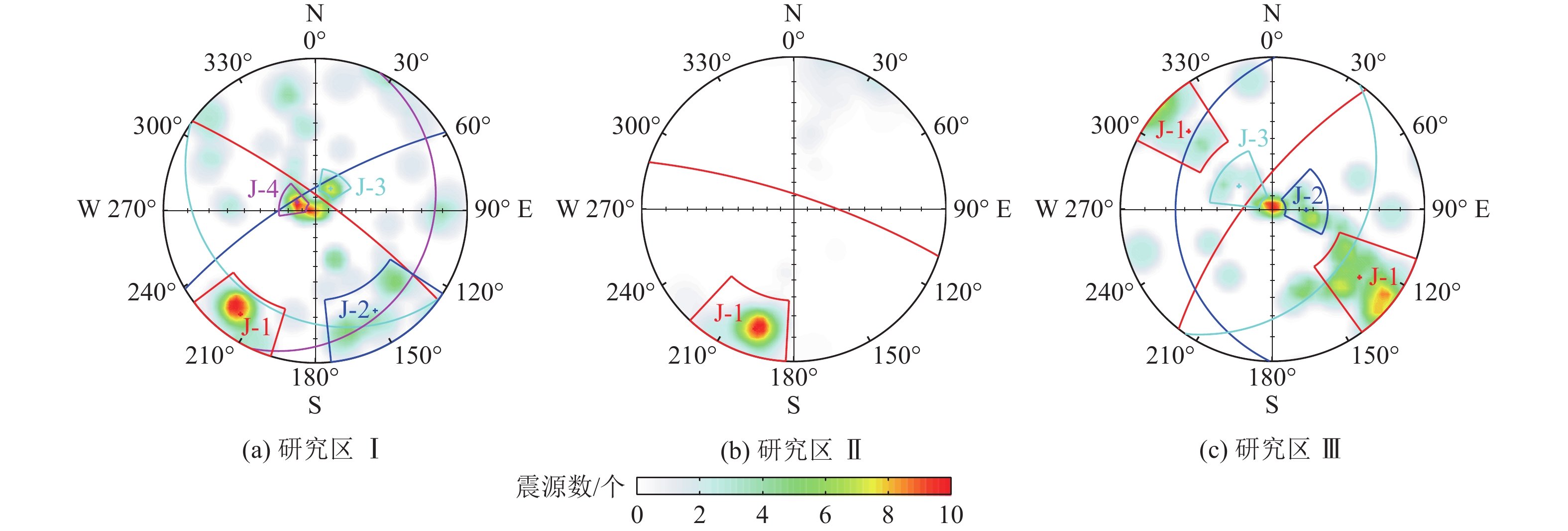
图 16 研究区Ⅰ、Ⅱ、Ⅲ主应力作用机制Figure 16. Acting mechanisms of principal stresses in study areas Ⅰ, Ⅱ, and Ⅲ随工作面推进，在不同大小、方位主应力作用下，结合震源破裂特征获取覆岩主断裂面分布，如图17所示。研究区Ⅰ覆岩断裂主要存在4个主要断裂方向，主破裂面为J-1(216°∠10°)，研究区Ⅱ覆岩整体沿方向J-1(198°∠11°)断裂滑移，研究区Ⅲ共有3个主要断裂方向，其中主破裂面为J-1(128°∠18°)。对于研究区Ⅰ、Ⅱ，覆岩断裂错动方向与工作面推进方向接近平行；研究区Ⅲ覆岩断裂方向与工作面推进方向近似成45°夹角，覆岩主破裂面沿工作面倾向呈“X”形分布。
![]()
图 17 研究区Ⅰ、Ⅱ、Ⅲ主应力作用下覆岩主破裂面方向分布Figure 17. Distributions of the Directions of the principal fracture planes of the overburden under principal stresses in study areas Ⅰ, Ⅱ, and Ⅲ根据应力反演结果，按文献[37]中方法将主应力进行缩放，从而得到研究区Ⅰ、Ⅱ、Ⅲ各个主应力相对大小，结合各主应力作用方位，进一步得到主应力变化对矿震触发的影响机制，如图18所示。
![]()
图 18 研究区Ⅰ、Ⅱ、Ⅲ矿震应力触发机制Figure 18. Stress-triggering mechanisms of mine earthquakes in study areas Ⅰ, Ⅱ, and Ⅲ对于研究区Ⅰ，工作面邻空回采进尺达到巨厚覆岩破断走向跨度后，最大主应力σ1较其他主应力显著增大，其作用方位为侧向采空区指向工作面，最大主应力单轴挤压作用于巨厚覆岩，从而诱发了“2·6”矿震。工作面继续推进，作用于巨厚覆岩的应力方位变化不大，但最大主应力相对其他主应力进一步增大，因巨厚覆岩初次破断诱发矿震后稳定性降低，最大主应力单轴挤压作用增大导致“10·30”矿震的发生。与“2·6”“10·30”矿震的应力触发机制不同，当工作面推进至研究区Ⅲ后，最大主应力降低明显，相对研究区Ⅰ、Ⅱ其作用方位在倾伏方向偏转约为45°，同时主应力σ2、σ3均出现不同程度偏转，分别来自侧向采空区及工作面前方的主应力σ1、σ3双轴挤压作用于失稳巨厚覆岩，是造成“2·4”矿震的主要原因。
当前1203工作面推进位置与1217工作面切眼平齐，后续工作面将邻更大侧向采空范围推进，仍存在因巨厚覆岩大尺度联动破断诱发矿震的风险。因此，重点分析上覆岩层破断演化特征、裂隙发育规律，及时反演作用于巨厚覆岩结构的应力分布，针对性开展以控制巨厚覆岩活动性为主的防震减震措施，定期评估巨厚覆岩应力状态，从而达到源头调控降载减震目的。
6 结 论
(1) 巨厚覆岩拉应力受采空区倾向长度影响最大，倾向、走向长度分别为600、800 m时达到巨厚覆岩破断力学条件，与矿震发生时工作面开采条件基本一致，表明巨厚覆岩破断运移为矿震孕育触发的动力和能量来源。工作面邻更大采空范围推进，巨厚覆岩破断尺度将进一步增加，工作面将面临更大矿震风险。
(2) 巨厚覆岩矿震孕育期间顶板逐层向上与侧向采空区联动破断，诱发微震震源破裂模式以纯张拉、纯压缩破裂为主。巨厚覆岩断裂诱发3起矿震震源矩张量以轴向拉伸成分占主导，占比均达到60 %以上，巨厚覆岩矿震孕育断裂特征呈显著张拉状态。
(3) 最大主应力较其他主应力显著增大，作用方位为侧向采空区指向工作面，单轴挤压作用于巨厚覆岩，从而导致内蒙古自治区鄂尔多斯呼吉尔特矿区某矿井“2·6”“10·30”矿震发生。最大主应力降低，倾伏方向发生大角度偏转，因侧向采空区及工作面前方的最大、最小主应力协同挤压失稳巨厚覆岩是造成“2·4”矿震的主要原因。
(4) 减弱巨厚覆岩活动性是降低矿震发生频度的关键。对于呼吉尔特矿区应重点分析邻空回采覆岩裂隙发育规律及其破断演化特征，及时反演作用于巨厚覆岩的应力场分布，开展以控制巨厚覆岩活动性为主的防震减震措施，定期评估巨厚覆岩应力状态，从而达到源头调控降载减震目的。
符号注释：
a为厚板长边的长度，m；A为厚板上某点的载荷在x轴方向的双三角级数形式；A为震源破裂面法向向量n组成的3×6阶矩阵；b为厚板短边的长度，m；B为厚板上某点的载荷在y轴方向的双三角级数形式；C为A在m=n=1取得的三角函数项；D为厚板抗弯刚度；E为弹性模量，MPa；f(xs)为等效作用力矢量密度；F为破坏岩体间水平推力；G为剪切模量，MPa；G(xr,xs)为弹性波传播介质脉冲响应；Gs, r为格林函数的空间导数；g为重力加速度，m/s2；h为巨厚覆岩上覆岩层厚度，m；H为板的厚度，m；i为布置在工作面附近的微震传感器；m为厚板坐标系中某点在x轴上的坐标；Ms,r为矩张量；Mx、My分别为厚板沿x、y轴方向的力矩，N·m；Mmax为厚板最大力矩，N·m；n为厚板坐标系中某点在y轴上的坐标；ni、nk、nj分别为法向向量在震源破裂面沿i、k、j方向的分量；n1、n2、n3分别为法向向量在震源破裂面坐标系中的分量；n为震源破裂面法向向量；q为厚板上覆载荷，MPa；qmn为作用于厚板上某点坐标(m，n)的载荷，MPa；tr为微震传感器接收到P波信号的时间，s；Tie为修正后的应力反演模型的有效牵引力；u为微震波形远场位移；v为震源破裂面滑移向量；V为震源应力反演方程；w为厚板挠度；XPCA为震动波形主成分信息构成的矩阵；XPCA(1)为波形第一主成分；Xi为第i个传感器接收到的微震波形矩阵；xr为微震传感器位置坐标；xs为震源位置坐标；δ、δik、δij分别为克罗内克函数及其在ik、ij平面的投影；μ为岩层泊松比；ρ为上覆岩层密度，kg/m3；σkj为应力分量σ在kj平面的投影；σije为修正后的应力反演模型的有效应力张量；σe为有效应力张量的矩阵形式；φ为ψx、ψy分别对x、y的导数之和；ψx、ψy分别为厚板上直线段在xy、yz平面内的转角，(°)；
$\nabla $ 为拉普拉斯算子。 -
![]()
图 2 沿工作面走向覆岩地层结构分布
注：数字为岩层厚度，m。
Fig. 2 Stratigraphic structure distribution of the overburden along the strike of the No.1203 mining face
![]()
图 3 工作面不同回采阶段矿震发生前后地表岩层移动规律
Fig. 3 Movement patterns of surface rock layers before and after the mine earthquakes in different mining stages of the mining face
![]()
图 4 巨厚覆岩厚板力学模型及其边界条件
Fig. 4 Thick-plate mechanical model of the extremely-thick overburden and its boundary conditions
![]()
图 5 不同采空条件巨厚覆岩拉应力极值分布
Fig. 5 Distribution of the extrema of tensile stresses in the significantly thick overburden under different goaf conditions
![]()
图 6 巨厚覆岩下部不同破断层位拉应力随工作面推进度变化关系
Fig. 6 Tensile stresses of different fractured layers in the lower part of the significantly thick overburden varying with the advancement of the No.1203 mining face
![]()
图 7 巨厚覆岩下部不同破断层位拉应力随工作面倾向长度的变化关系
Fig. 7 Tensile stresses of different fractured horizons in the lower portion of the significantly thick overburden varying with the inclination length of the No.1203 mining face
![]()
图 10 震源破裂类型判识准则
Fig. 10 Criteria for discriminating the fracture types of seismic sources
![]()
图 11 不同回采阶段震源类型CLVD−ISO钻石图
Fig. 11 CLVD-ISO diamond diagrams showing the fracturing types of seismic sources in different mining stages
![]()
图 13 研究区Ⅰ、Ⅱ、Ⅲ震源破裂面产状信息
Fig. 13 Information on the occurrence of fracture planes of seismic sources in study areas Ⅰ, Ⅱ, and Ⅲ
![]()
图 14 研究区Ⅰ、Ⅱ、Ⅲ应力场分布情况
Fig. 14 Distributions of stress fields in study areas Ⅰ, Ⅱ, and Ⅲ
![]()
图 15 研究区Ⅰ、Ⅱ、Ⅲ应力形因子分布情况
Fig. 15 Distributions of stress shape factors in study areas Ⅰ, Ⅱ, and Ⅲ
![]()
图 16 研究区Ⅰ、Ⅱ、Ⅲ主应力作用机制
Fig. 16 Acting mechanisms of principal stresses in study areas Ⅰ, Ⅱ, and Ⅲ
![]()
图 17 研究区Ⅰ、Ⅱ、Ⅲ主应力作用下覆岩主破裂面方向分布
Fig. 17 Distributions of the Directions of the principal fracture planes of the overburden under principal stresses in study areas Ⅰ, Ⅱ, and Ⅲ
![]()
图 18 研究区Ⅰ、Ⅱ、Ⅲ矿震应力触发机制
Fig. 18 Stress-triggering mechanisms of mine earthquakes in study areas Ⅰ, Ⅱ, and Ⅲ
表 1 工作面不同回采阶段主应力分布情况
Table 1 Distributions of principal stresses in different mining stages of the No.1203 mining face
主应力 方位角α/(°)；倾伏角θ/(°) 研究区Ⅰ 研究区Ⅱ 研究区Ⅲ σ1 153.83；12.98 143.96；10.48 151.72；53.79 σ2 275.42；66.24 284.66；76.56 335.94；36.13 σ3 59.14；19.54 52.41；8.32 244.47；2.01 
下载: 导出CSV
-
[1] 曹安业,窦林名,白贤栖,等. 我国煤矿矿震发生机理及治理现状与难题[J]. 煤炭学报,2023,48(5):1894−1918. CAO Anye,DOU Linming,BAI Xianxi,et al. State-of-the-art occurrence mechanism and hazard control of mining tremors and their challenges in Chinese coal mines[J]. Journal of China Coal Society,2023,48(5):1894−1918.
[2] 白贤栖,曹安业,杨耀,等. 高位巨厚覆岩运移规律及矿震触发机制研究[J]. 煤炭科学技术,2023,51(3):10−20. BAI Xianxi,CAO Anye,YANG Yao,et al. Study on movement law of extremely thick strata and triggering mechanism of mine earthquakes[J]. Coal Science and Technology,2023,51(3):10−20.
[3] 杨耀,曹安业,白贤栖,等. 深井巨厚覆岩邻空采动强矿震孕育发生机理[J]. 煤炭科学技术,2023,51(12):220−231. YANG Yao,CAO Anye,BAI Xianxi,et al. Occurrence mechanism of strong mining tremors under mining near goaf in deep mine with extremely thick strata[J]. Coal Science and Technology,2023,51(12):220−231.
[4] 李斌,任玺宁,崔春兰,等. 补连塔煤矿中生界高分辨率层序地层与沉积环境演化[J]. 地质科学,2022,57(4):1262−1285. LI Bin,REN Xining,CUI Chunlan,et al. High-resolution sequence stratigraphy and sedimentary environment evolution of Mesozoic in Bulianta Coal Mine[J]. Chinese Journal of Geology (Scientia Geologica Sinica),2022,57(4):1262−1285.
[5] 朱斯陶,刘金海,姜福兴,等. 我国煤矿顶板运动型矿震及诱发灾害分类、预测与防控[J]. 煤炭学报,2022,47(2):807−816. ZHU Sitao,LIU Jinhai,JIANG Fuxing,et al. Classification,prediction,prevention and control of roof movement-type mine earthquakes and induced disasters in China’s coal mines[J]. Journal of China Coal Society,2022,47(2):807−816.
[6] 曹安业,陈凡,刘耀琪,等. 冲击地压频发区矿震破裂机制与震源参量响应规律[J]. 煤炭学报,2022,47(2):722−733. CAO Anye,CHEN Fan,LIU Yaoqi,et al. Response characteristics of rupture mechanism and source parameters of mining tremors in frequent coal burst area[J]. Journal of China Coal Society,2022,47(2):722−733.
[7] 吴顺川,黄小庆,陈钒,等. 岩体破裂矩张量反演方法及其应用[J]. 岩土力学,2016,37(增刊1):1−18. WU Shunchuan,HUANG Xiaoqing,CHEN Fan,et al. Inversion method of fracture moment tensor of rock mass and its application[J]. Rock and Soil Mechanics,2016,37(Sup.1):1−18.
[8] 白贤栖,曹安业,刘耀琪,等. 基于震源机制解析的巨厚覆岩矿震破裂机制[J]. 煤炭学报,2023,48(11):4024−4035. BAI Xianxi,CAO Anye,LIU Yaoqi,et al. Mine earthquake mechanism of extremely thick strata based on focal memchanism analysis[J]. Journal of China Coal Society,2023,48(11):4024−4035.
[9] 刘耀琪,曹安业,王常彬,等. 基于震源机制与定位误差校准的冲击地压危险预测方法[J]. 煤炭学报,2023,48(5):2065−2077. LIU Yaoqi,CAO Anye,WANG Changbin,et al. Prediction method of coal burst risk based on focal mechanism and location error calibration[J]. Journal of China Coal Society,2023,48(5):2065−2077.
[10] MUKUHIRA Y,FUSE K,NAOI M,et al. Hybrid focal mechanism determination:Constraining focal mechanisms of injection induced seismicity using in situ stress data[J]. Geophysical Journal International,2018,215(2):1427−1441. DOI: 10.1093/gji/ggy333
[11] GLASGOW M E,SCHMANDT B,BILEK S L. Cascading multi-segment rupture in an injection-induced earthquake sequence with a Mw 5.3 mainshock[J]. Earth and Planetary Science Letters,2023,620:118335. DOI: 10.1016/j.jpgl.2023.118335
[12] 李铁,张山林,李守峰,等. 华亭煤矿强矿压力学机制与防治对策[J]. 煤炭学报,2016,41(5):1093−1098. LI Tie,ZHANG Shanlin,LI Shoufeng,et al. Mechanism and control measures of rockburst in Huating Coal Mine[J]. Journal of China Coal Society,2016,41(5):1093−1098.
[13] 刘洋,陆菜平,王华,等. 不规则煤柱变形破坏机理矩张量反演研究[J]. 采矿与安全工程学报,2023,40(6):1201−1209. LIU Yang,LU Caiping,WANG Hua,et al. Moment tensor inversion study on deformation and failure mechanism of the irregular coal pillar[J]. Journal of Mining & Safety Engineering,2023,40(6):1201−1209.
[14] 唐超,李庶林,周梦婧,等. 基于微震监测的应力场反演方法及其工程应用研究[J]. 岩土工程学报,2021,43(9):1730−1738. TANG Chao,LI Shulin,ZHOU Mengjing,et al. Stress inversion based on microseismic monitoring and its engineering application[J]. Chinese Journal of Geotechnical Engineering,2021,43(9):1730−1738.
[15] WANG Chaoliang,LIANG Chuntao,LIAO Jiangtao,et al. Temporary stress regime reversal immediately after the complete release of the localized compressive stress by the 2021 Luxian Ms 6.0 earthquake,Sichuan Basin[J]. Earth and Planetary Science Letters,2023,618:118282. DOI: 10.1016/j.jpgl.2023.118282
[16] CHANG Chandong. Identifying subsurface fault planes via a stress inversion of earthquake focal mechanisms[J]. Geophysical Journal International,2023,236(2):1106−1124. DOI: 10.1093/gji/ggad474
[17] MAGEN Y,BAER G,ZIV A,et al. Fault coalescence,slip distribution,and stress drop of the February 2023 southeast Türkiye earthquakes from joint inversion of SAR,GNSS,and burst overlap interferometry[J]. Seismological Research Letters,2024,95(2A):680−696. DOI: 10.1785/0220230271
[18] LIZUREK G,WISZNIOWSKI J,GIANG N V,et al. Clustering and stress inversion in the Song Tranh 2 Reservoir,Vietnam[J]. Bulletin of the Seismological Society of America,2017,107(6):2636−2648. DOI: 10.1785/0120170042
[19] 龙述尧,姜琛. 中厚板理论的适用范围和精确程度的研究[J]. 湖南大学学报(自然科学版),2012,39(1):37−41. LONG Shuyao,JIANG Chen. Research on the applicable range and accuracy of moderately thick plate theory[J]. Journal of Hunan University (Natural Sciences),2012,39(1):37−41.
[20] 周坤友. 巨厚承压含水关键层的作用效应及疏水调压聚能诱冲机理[D]. 徐州:中国矿业大学,2022. ZHOU Kunyou. Effect of huge thick confined water-bearing key layer and mechanism of hydrophobic pressure regulating accumulation energy induction and flushing[D]. Xuzhou:China University of Mining and Technology,2022.
[21] 贺广零. 基于厚板理论的水平煤层顶板临界厚度的分析[J]. 地下空间与工程学报,2009,5(4):659−663. HE Guangling. Determination of critical thickness of stiff roof in coal mine based on thick plate theory[J]. Chinese Journal of Underground Space and Engineering,2009,5(4):659−663.
[22] 赵国彦,周士祥. 基于厚板理论的滨海开采顶板安全厚度确定[J]. 中国地质灾害与防治学报,2015,26(4):60−66. ZHAO Guoyan,ZHOU Shixiang. Determining safe thickness of roof in subsea mining based on thick plate theory[J]. The Chinese Journal of Geological Hazard and Control,2015,26(4):60−66.
[23] 张帝. 基于多钻孔联合建模的鄂尔多斯矿区巨厚覆岩型矿震发生机制研究[D]. 徐州:中国矿业大学,2023. ZHANG Di. Study on the mechanism of super-thick overburden type mine earthquake in Ordos mining area based on multi-borehole joint modeling[D]. Xuzhou:China University of Mining and Technology,2023.
[24] 曹安业,杨旭,王常彬,等. 基于深度迁移学习的矿山微震到时精确拾取与自动定位策略[J]. 煤炭学报,2023,48(12):4393−4405. CAO Anye,YANG Xu,WANG Changbin,et al. High-precision phase picking and automatic source locating method for seismicity in mines based on deep transfer learning[J]. Journal of China Coal Society,2023,48(12):4393−4405.
[25] VAVRYČUK V,ADAMOVÁ P,DOUBRAVOVÁ J,et al. Moment tensor inversion based on the principal component analysis of waveforms:Method and application to microearthquakes in West Bohemia,Czech republic[J]. Seismological Research Letters,2017,88(5):1303−1315. DOI: 10.1785/0220170027
[26] LIU Yaoqi,CAO Anye,WANG Changbin,et al. Cluster analysis of moment tensor solutions and its application to rockburst risk assessment in underground coal mines[J]. Rock Mechanics and Rock Engineering,2023,56(9):6709−6734. DOI: 10.1007/s00603-023-03388-y
[27] GILBERT F. Excitation of the normal modes of the earth by earthquake sources[J]. Geophysical Journal International,1971,22(2):223−226. DOI: 10.1111/j.1365-246X.1971.tb03593.x
[28] ZHAO Yong,YANG Tianhong,ZHANG Penghai,et al. Inversion of seepage channels based on mining-induced microseismic data[J]. International Journal of Rock Mechanics and Mining Sciences,2020,126:104180. DOI: 10.1016/j.ijrmms.2019.104180
[29] VAVRYČUK V. Inversion for parameters of tensile earthquakes[J]. Journal of Geophysical Research:Solid Earth,2001,106(B8):16339−16355. DOI: 10.1029/2001JB000372
[30] BOTT M H P. The mechanics of oblique slip faulting[J]. Geological Magazine,1959,96(2):109−117. DOI: 10.1017/S0016756800059987
[31] 杨耀,曹安业,刘耀琪,等. 联合震源破裂信息反演解析巨厚覆岩强矿震应力触发机制[J/OL]. 煤炭学报,2024:1−17[2024-06-29]. https://doi.org/10.13225/j.cnki.jccs.2024.0350. YANG Yao,CAO Anye,LIU Yaoqi,et al. Stress triggering mechanism of strong mine earthquake in huge thick strata revealed by inversion of joint source rupture information[J/OL]. Journal of China Coal Society,2024:1−17[2024-06-29]. https://doi.org/10.13225/j.cnki.jccs.2024.0350.
[32] JIA S Q,EATON D W,WONG R C. Stress inversion of shear-tensile focal mechanisms with application to hydraulic fracture monitoring[J]. Geophysical Journal International,2018,215(1):546−563. DOI: 10.1093/gji/ggy290
[33] SASAKI S,KAIEDA H. Determination of stress state from focal mechanisms of microseismic events induced during hydraulic injection at the Hijiori hot dry rock site[J]. Pure and Applied Geophysics,2002,159(1):489−516. DOI: 10.1007/PL00001262
[34] VAVRYČUK V. Iterative joint inversion for stress and fault orientations from focal mechanisms[J]. Geophysical Journal International,2014,199(1):69−77. DOI: 10.1093/gji/ggu224
[35] VAVRYČUK V. Moment tensor decompositions revisited[J]. Journal of Seismology,2015,19(1):231−252. DOI: 10.1007/s10950-014-9463-y
[36] CONDER J A,ARCINIEGAS C A. Conjugate faulting in the Wabash valley fault zone exhibited by the 20 November 2012 mb3.6 earthquake,a Mt. Carmel late aftershock[J]. Seismological Research Letters,2017,88(4):1203−1209. DOI: 10.1785/0220170021
[37] VAVRYČUK V,BOUCHAALA F,FISCHER T. High-resolution fault image from accurate locations and focal mechanisms of the 2008 swarm earthquakes in West Bohemia,Czech Republic[J]. Tectonophysics,2013,590:189−195. DOI: 10.1016/j.tecto.2013.01.025
-
期刊类型引用(2)
1. 杨承伟，胡军，王成虎，杨长林，高桂云. 丽江—大理地区现代应力场特征分析. 凿岩机械气动工具. 2025(01): 174-177 . 
百度学术
2. 谭云亮，张修峰，范德源，刘学生，朱斯陶，牟宗龙，陈洋. 沿空侧向覆岩结构改性防冲机理与实践. 煤炭学报. 2025(01): 209-223 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 177
- HTML全文浏览量: 20
- PDF下载量: 53
- 被引次数: 2
