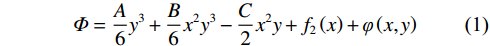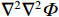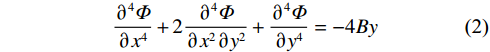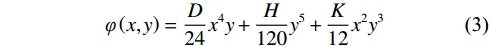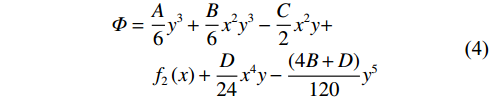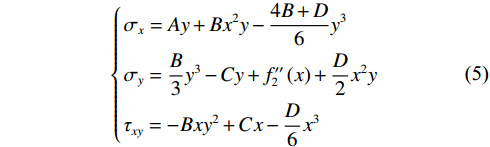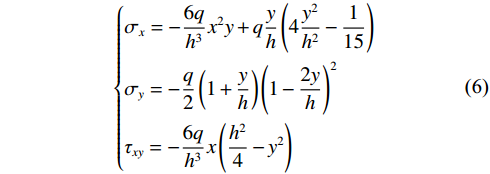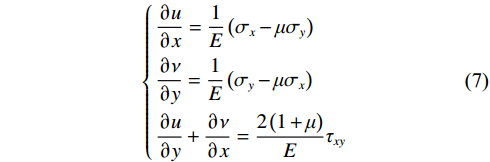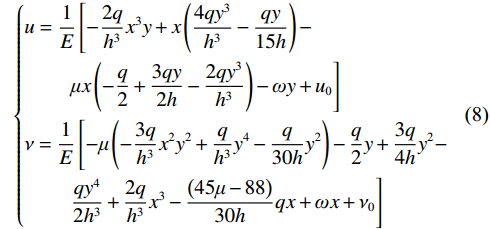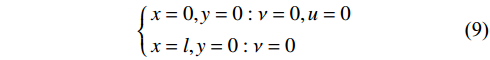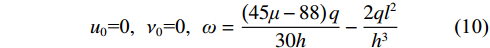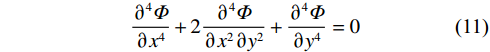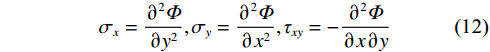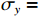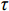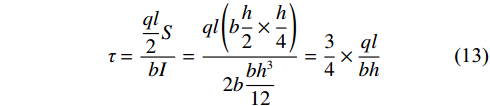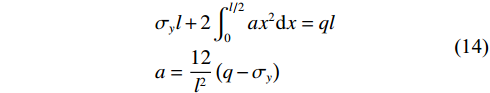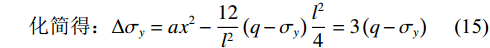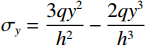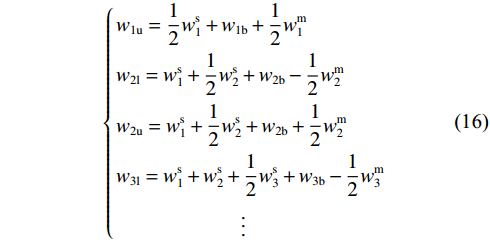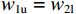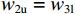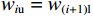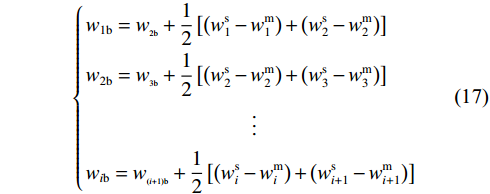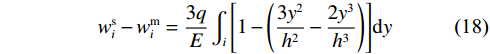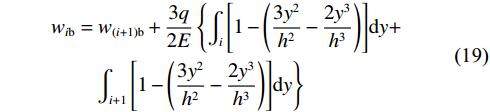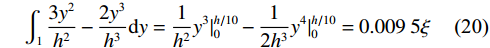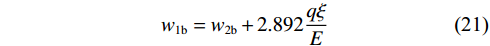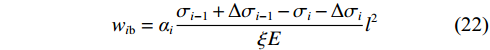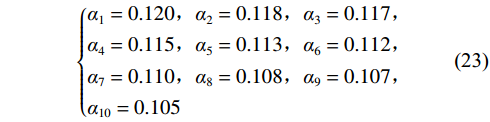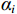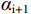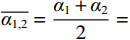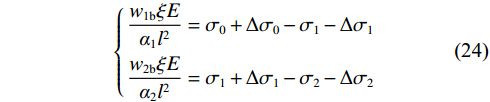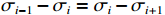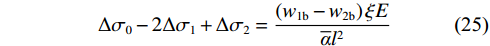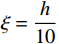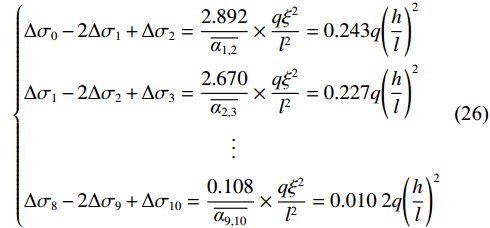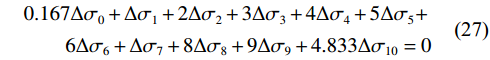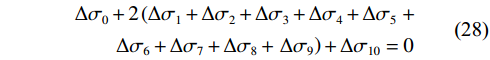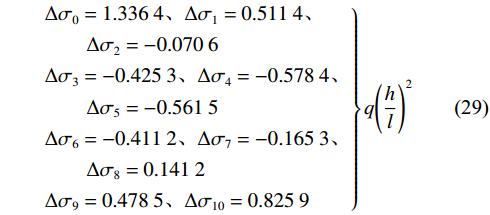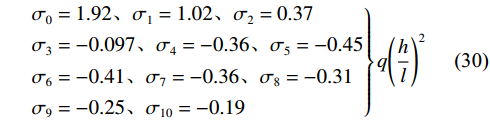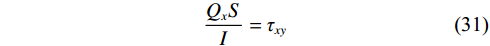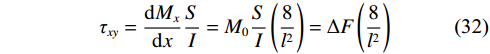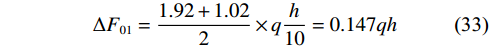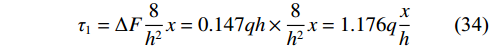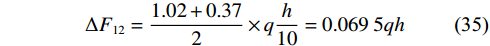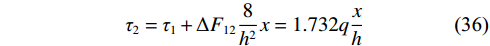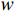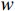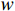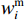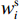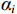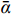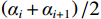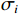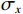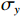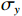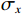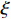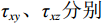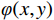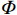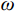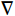Deep beam theory-based mechanical analysis of water-resisting key strata of coal seam floors in a deep mining environment
-
摘要:目的
随着矿井开采深度增加，来自高承压岩溶水威胁增大，导致煤层工作面出现涌水、突水等水害现象，分析深部开采环境下煤层底板隔水关键层抵抗水压力强度是解决这一现象的重要内容之一。
方法为解决此问题，将隔水底板简化为岩梁模型，并运用深梁理论解决深部开采突水预测中的岩梁模型问题，采用理论分析和数值模拟相结合的方法，根据深梁弯曲力学特点，结合前人研究成果，将深梁条分成浅梁，通过弹性力学单根浅梁受力分布形式假定层间挤压应力σy为三次函数，给出深梁弯曲应力求解的条分技术，并将计算结果与弹性力学解、FLAC3D模拟结果进行对比。
结果和结论结果表明，深梁条分解得到的应力及位移与数值解结果趋势更为接近，计算结果更为精确，相对误差均在10%以内，同时，随着条分层数增加，精度也增加，但提高幅度逐渐降低，因此，工程应用中针对深部岩梁模型条分到一定程度即可；随着高跨比不断增加，精度误差也在增加，说明条分层宽度不宜过大，否则造成误差增加；底板隔水关键层实例表明，当隔水关键层高跨比大于0.2时，为典型的深梁问题，常规弹性力学的最大拉应力求解结果误差较大，相对误差达到40.6%，给正确判定关键层突水危险性带来不利影响，此时采用深梁条分法求解应力精度较高，可为深部煤层底板突水预测研究起到重要的指导作用。
Abstract:ObjectiveAn increase in the mining depth of mines poses a more serious threat from highly confined karst water, resulting in water hazards like water inflow and inrushes on the mining faces of coal seams. The key content used to address this issue is to analyze the water pressure resistance of the water-resisting key stratum of the coal seam floor in a deep mining environment.
MethodsThis study simplified a water-resisting key stratum into a rock beam model and then dealt with this model using the deep beam theory in the prediction of water inrushes in deep mining. Specifically, by combining theoretical analysis with numerical simulation, this study sliced the deep beam into shallow beams based on the bending mechanical characteristics of the deep beam and previous research results. Then, according to the elastic force distribution of various shallow beams, it was assumed that the interlayer compressive stress σy was a cubic function and presented a slicing technique to determine the bending stress of the deep beam. Finally, the calculated results were compared with the elastic mechanic solutions and the FLAC3D simulation results.
Results and ConclusionsThe results indicate that the stress and displacement obtained through the slicing of the deep beam were closer to the numerical simulation results, yielding more accurate calculation results with relative error less than 10%. As the number of shallow beams increased, more accurate calculation results were obtained. However, the increased amplitude of the accuracy gradually decreased, necessitating appropriate slicing of the deep rock beam model in engineering applications. Furthermore, errors increased with the height/span length (h/l) ratio. Therefore, appropriate slicing widths are required, otherwise errors will increase. An example of a water-resisting key stratum of a coal seam floor demonstrates that a h/l ratio exceeding 0.2 suggests a typical deep beam. In this case, the maximum tensile stress calculated using conventional elastic mechanics exhibited relative error reaching up to 40.6%, exerting a negative impact on properly determining the risks of water inrushes in the water-resisting key stratum. In contrast, the deep-beam slicing method manifested higher accuracy in solving stress, thus serving as a significant guide for the prediction of water inrushes from deep coal seam floors.
-
Keywords:
- deep mining /
- floor aquiclude /
- rock beam model /
- deep beam /
- numerical simulation /
- water inrush prediction
-
煤矿开采突水事故一直是制约我国煤矿安全开采的重要影响因素。随着浅部煤炭资源日益减少，我国煤矿、天然气等资源的开采深度以每年10~25 m的速度逐渐向深部延伸，目前已探明煤炭资源量超过5.9万亿t，其中深部资源(千米以下)占比超过50%，未来包括西部在内的全国70%煤炭产能都将进入深部开采[1]。随着开采深度的增加，岩溶、顶板砂岩、煤系砂岩等各种含水层问题影响煤矿工作面的安全开采，煤层底板突水预测预报研究一直未得到质的突破，底板重大突水事故仍偶有发生[2]。深部开采岩石及围岩应力较为复杂，基于“三高一扰动”[3]的力学环境，与浅部煤层开采中的岩石力学行为和地质灾害明显不同，围岩大变形、水压增大、冲击地压、岩爆和分区破裂化等大量非线性力学现象在深部地区出现，开采工作面的地应力水平也不断上升，围岩应力逐渐由稳定状态转变为非稳定状态，基于材料力学静态理论建立的岩石力学梁板理论不再适用于深部复杂环境[4]。众多学者针对底板水害问题开展了大量研究[5-9]，钱鸣高等[10]提出关键层理论，认为岩层控制的关键层理论可以用于采场底板的突水治理研究，对于关键层的力学分析，通常考虑水压作用导致的煤层弯曲变形及裂缝产生，因此，煤层底板抵抗水压力的能力是关键。孙建等[11]依据隔水关键层理论，分析了底板倾斜隔水关键层的挠度特性、应力分布及其破断失稳特征，确定了倾斜采场底板突水危险区域；鲁海峰等[12]针对底板隔水层岩体层状结构特点，结合梁板理论将隔水关键层简化为固定梁，通过考虑地应力作用系统总结其沿层理面剪切出现分层、端部压剪及弯拉等破坏模式，并给出相应力学判据；冯梅梅等[13]依托梁板理论及岩层受力情况，将隔水关键层简化为两端固支组合梁模型，并分析在均布荷载作用下各类岩层组合对其隔水性能的影响规律；孙强等[14]基于充填开采隔水关键层研究，建立了开采隔水关键层非线性渗流稳定性力学模型，通过研究隔水关键层耦合作用，给出了隔水关键层非线性渗流失稳与临界充实率的定量关系。
上述底板隔水关键层理论研究中，一般将隔水层视为浅梁，运用梁板理论进行应力与变形的求解，从而达到突水预测目的。众所周知，浅梁是指高跨比小于0.2的梁，在浅梁的受力变形分析中，已有研究多采用欧拉梁理论[15-18]，基于平截面假定认为截面的转动等于挠度曲线切线的斜率，且一般长壁开采工作面底板通常被简化为浅梁模型，此时采用欧拉梁理论更为适用，而当高跨比≥0.2的杆件属于深梁研究范围[19]，铁木辛柯梁理论[20]认为在深梁受力分析中，应考虑梁在挠曲和扭转过程中横截面的变形，即剪切力是不可忽略的主要因素，由于深梁与其高跨比有关，荷载作用会使应力重分布，且不呈线性相关，梁的正截面应变不符合平截面假定。实际上，煤矿防治水工程中运用浅梁理论解决深梁情况，计算出的应力和变形具有较大误差，虽然国内外学者对于煤层底板突水理论的研究如力学基础理论[21-22]、防治技术[23-24]、隐伏断层分类[25-26]和监测预警[27-28]等在不断增加，但运用深梁理论分析关键层的应力、变形等成果较少，基于欧拉理论的解析解大多假定在荷载作用下梁各纵向纤维不产生挤压和压缩，有一定的局限性，而深梁力学分析需考虑层间挤压变形[19]，因此，针对深部开采隔水关键层底板受力分析需要展开进一步研究，以正确评价隔水底板突水失稳的危险性。
为此，笔者提出运用深梁理论解决突水预测中的岩梁模型问题，根据深梁弯曲力学特点，将深梁沿跨度方向条分成若干浅梁，考虑层间力的影响给出深梁弯曲应力求解的条分技术，采用弹性力学中应力函数法和深梁条分解法分别对关键层受力问题进行分析，并将计算结果与FLAC3D模拟结果进行对比，分析深梁弯曲应力求解精度，最后将研究成果应用到现场底板关键层力学分析，以期为矿井底板突水预测提供理论支撑。
1 煤层底板关键层岩梁模型建立
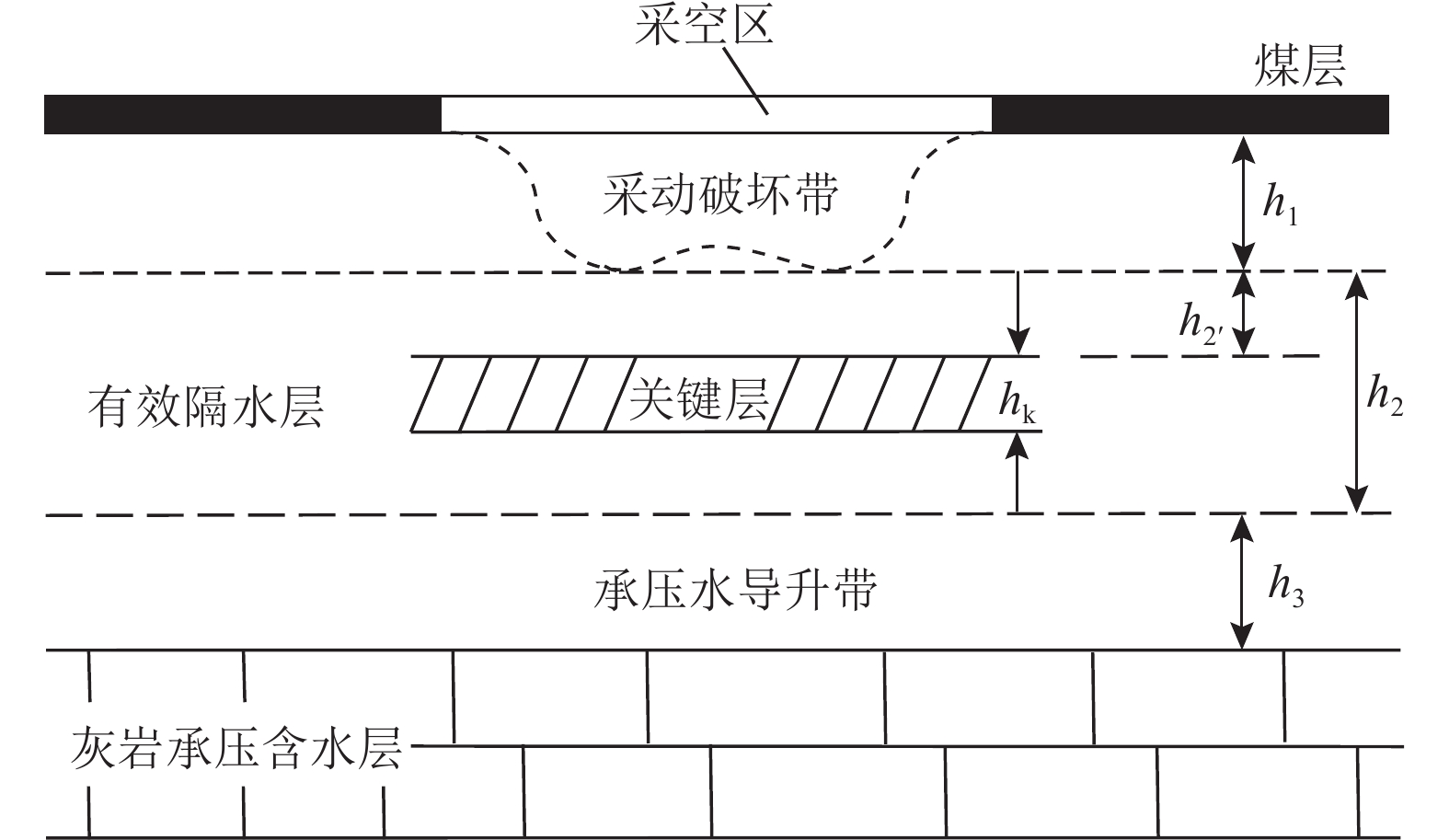
依据“下三带”理论，在煤层开采过程中，承压水体上煤层底板岩层由上到下形成底板采动破坏带、有效隔水层保护带和承压水导升带。一般认为隔水带起主要阻水保护作用。如图1所示，煤层工作面回采过程中，由于采动矿压作用导致工作面底板一定范围内的岩体破坏，形成采动破坏带，其最大高度为h1。同时，由于工作面开采和承压水影响，含水层中承压水沿原始裂隙上升，形成承压水导升带，其最大高度为h3。当工作面底板未发生突水时则存在完整隔水层带，其最大高度为h2，h2’则为关键层到底板采动破坏带底界的高度。基于隔水关键层理论，对于底板完整隔水层中总能找到某一处关键岩层起隔水能力，这种岩层视为关键层[29-31]，其厚度为hk。对于底板完整隔水层的隔水能力，通常将问题转化为对承载能力最强的岩层进行受力分析，一般采用梁弯曲理论求解关键层应力，并根据受力极限判定突水与否。采用岩梁模型时，当采空跨度和关键层厚度hk相差不大时，此时关键层弯曲不属于浅梁范畴，而是典型的深梁问题。
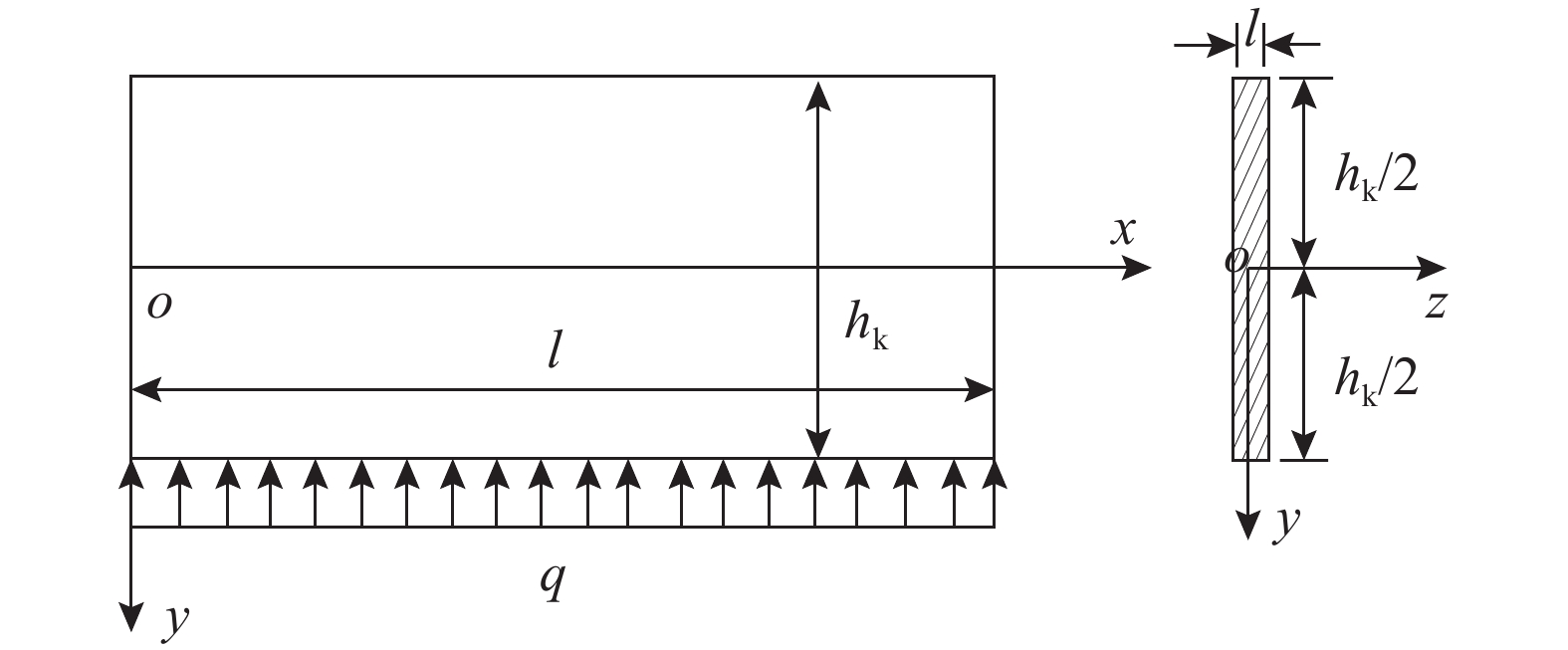
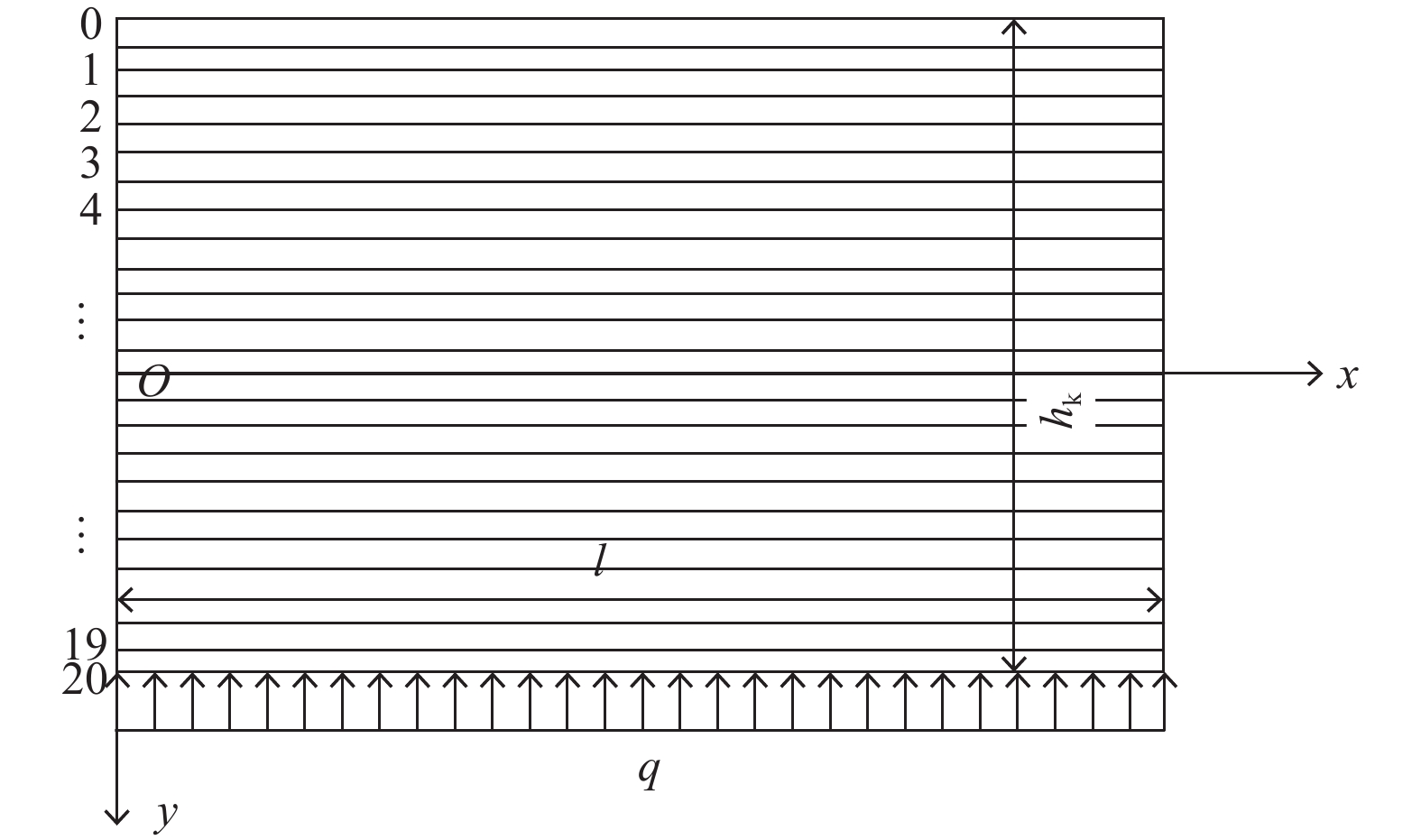
鉴于煤系岩体裂隙发育的广泛性，将岩梁端部视为铰支座是一种有效的处理方式[32-33]，故可将承压水上采煤底板隔水关键层视为简支深梁，运用深梁理论探究底板的受力及其破坏形式，为突水预测提供理论依据。根据上述理论建立如图2所示关键层简支梁模型，其坐标系以关键层左边截面中点为原点O，横向x轴为梁长方向，竖向y轴为梁高方向，底部受均布水压力p的作用，其中l代表初次来压步距，hk为关键层厚度，底板煤层取单位宽度1，底板平均容重为γ，则关键层简支梁模型的下表面受到均布荷载q为水压p减去关键层上覆岩层重力：q=p−γ(h1+h2'+hk)。
![]()
图 2 2种解法下隔水关键层简支梁力学模型Figure 2. Mechanical model of a simply supported beam for a key aquiclude under two solutions工程中将高跨比≥0.2的杆件归属于深梁范围，为便于分析，本文将高跨比定义为h/l，即关键层厚度与初次来压步距的比值，研究弹性力学中应力函数法和深梁条分解的求解精度，并探讨随着高跨比的增大及分层层数增加，深梁条分解的精度变化规律。
2 两种解法的解析解及精度评价
2.1 应力函数法
应力函数法是弹性力学中解决梁问题常用的方法之一，该方法在满足平衡微分及协调方程前提下以应力协调条件推导函数表达式，同时根据物体边界建立协调物理、几何方程进行求解，推导应力与位移分量。主要计算过程如下。
基于材料力学公式修正[34-35]，得到弹性力学在均布荷载下简支梁的应力函数式为：
$$ \varPhi = \frac{A}{6}{y^3} + \frac{B}{6}{x^2}{y^3} - \frac{C}{2}{x^2}y + {f_2}\left( x \right) + \varphi \left( {x,y} \right) $$ (1) 将上式代入双调和方程
$ {\nabla }^{2}{\nabla }^{2}\varPhi $ =0[36]，得到：$$ \frac{{{\partial ^4}\varPhi }}{{\partial {x^4}}} + 2\frac{{{\partial ^4}\varPhi }}{{\partial {x^2}\partial {y^2}}} + \frac{{{\partial ^4}\varPhi }}{{\partial {y^4}}} = - 4By $$ (2) $$ \varphi \left( {x,y} \right) = \frac{D}{{24}}{x^4}y + \frac{H}{{120}}{y^5} + \frac{K}{{12}}{x^2}{y^3} $$ (3) 简化得：
$$ \begin{aligned} & \varPhi = \frac{A}{6}{y^3} + \frac{B}{6}{x^2}{y^3} - \frac{C}{2}{x^2}y + \\ &\qquad {f_2}\left( x \right) + \frac{D}{{24}}{x^4}y - \frac{{\left( {4B + D} \right)}}{{120}}{y^5} \end{aligned} $$ (4) 对应的应力分量为：
$$ \left\{ \begin{gathered} {\sigma _x} = Ay + B{x^2}y - \frac{{4B + D}}{6}{y^3} \\ {\sigma _y} = \frac{B}{3}{y^3} - Cy + f''_{\text{2}}\left( {{x}} \right) + \frac{D}{2}{x^2}y \\ {\tau _{xy}} = - Bx{y^2} + Cx - \frac{D}{6}{x^3} \\ \end{gathered} \right. $$ (5) 根据上下两面边界条件以及两端边界条件，稍加整理后得到应力表达式：
$$ \left\{\begin{aligned} & {\sigma _x} = - \frac{{6q}}{{{h^3}}}{x^2}y + {{q}}\frac{y}{h}\left( {4\frac{{{y^2}}}{{{h^2}}} - \frac{1}{{15}}} \right) \\ & {\sigma _y} = - \frac{q}{2}\left( {1 + \frac{y}{h}} \right){\left( {1 - \frac{{2y}}{h}} \right)^2} \\ & {\tau _{xy}} = - \frac{{6q}}{{{h^3}}}x\left( {\frac{{{h^2}}}{4} - {y^2}} \right)\end{aligned} \right. $$ (6) 已知应力与位移关系式如下：
$$ \left\{\begin{gathered} \frac{{\partial u}}{{\partial x}} = \frac{1}{E}\left( {{\sigma _x} - \mu {\sigma _y}} \right) \\ \frac{{\partial \nu }}{{\partial y}} = \frac{1}{E}\left( {{\sigma _y} - \mu {\sigma _x}} \right) \\ \frac{{\partial u}}{{\partial y}} + \frac{{\partial \nu }}{{\partial x}} = \frac{{2\left( {1 + \mu } \right)}}{E}{\tau _{xy}} \\ \end{gathered} \right.$$ (7) 将式(6)、式(7)联立，积分后得到某受力点在关键层上位移表达式为：
$$ \left\{ \begin{split} & u = \frac{1}{E}\left[ - \frac{{2q}}{{{h^3}}}{x^3}y + x\left( {\frac{{4q{y^3}}}{{{h^3}}} - \frac{{qy}}{{15h}}} \right) -\right.\\ &\qquad \left.\mu x\left( { - \frac{q}{2} + \frac{{3qy}}{{2h}} - \frac{{2q{y^3}}}{{{h^3}}}} \right) - \omega y + {u_{\text{0}}} \right] \\ & \nu = \frac{1}{E}\left[ - \mu \left( { - \frac{{3q}}{{{h^3}}}{x^2}{y^2} + \frac{q}{{{h^3}}}{y^4} - \frac{q}{{30h}}{y^2}} \right) - \frac{q}{2}y + \frac{{3q}}{{4h}}{y^2} -\right.\\ &\qquad \left.\frac{{q{y^4}}}{{2{h^3}}} + \frac{{2q}}{{{h^3}}}{x^3} - \frac{{\left( {45\mu - 88} \right)}}{{30h}}qx + \omega x + {\nu _0} \right]\end{split} \right. $$ (8) 根据简支梁边界条件：
$$ \left\{\begin{gathered} x = 0,y = 0:\nu = 0,u = 0 \\ x = l,y = 0:\nu = 0 \\ \end{gathered}\right. $$ (9) 将式(9)代入式(8)可得：
$$ {u}_{0}\text{=0},\;\;{\nu }_{0}\text{=0},\;\;\omega =\frac{\left(45\mu -88\right)q}{30h}-\frac{2q{l}^{2}}{{h}^{3}} $$ (10) 2.2 深梁条分解
深梁理论解的方法已有状态空间法[37]、杆件力学法[38]以及级数解法[39]等，但目前系统讨论深梁应力求解精度、中性轴变化规律，特别是重力影响下的求解方法的研究成果较少。在常规梁力学解中，浅梁由于不考虑层间挤压应力σy，无法解决高跨比不断增大的深梁问题，为此本文在文献[38]研究的基础上，同样将深梁在沿跨度方向条分成若干浅梁，根据式(6)可知，假设层间挤压应力σy在跨中沿截面高度按三次抛物线分布是可行的，因此将层间挤压应力σy假定为弹性力学中的三次函数分布，同时考虑深梁重力作用，给出重力影响下的深梁条分解。以下将对深梁条分解进行说明。
常体力情况下应力函数Φ表示的平面问题基本方程式 [36]为：
$$ \frac{{{\partial ^4}\varPhi }}{{\partial {x^4}}} + 2\frac{{{\partial ^4}\varPhi }}{{\partial {x^2}\partial {y^2}}} + \frac{{{\partial ^4}\varPhi }}{{\partial {y^4}}} = 0 $$ (11) 各应力分量可表示为：
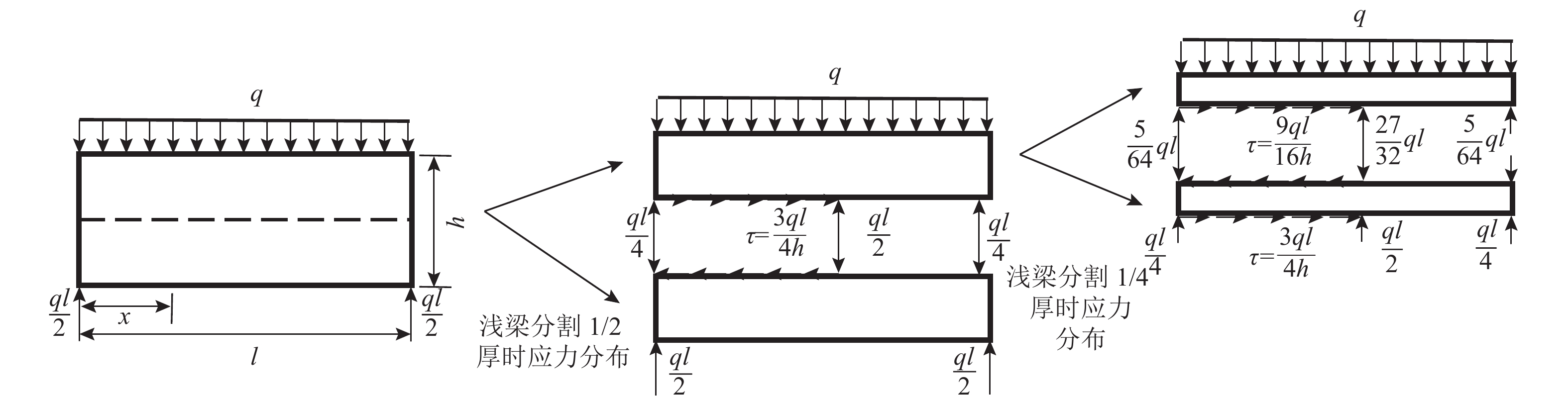
$$ {\sigma _x} = \frac{{{\partial ^2}\varPhi }}{{\partial {y^2}}},{\sigma _y} = \frac{{{\partial ^2}\varPhi }}{{\partial {x^2}}},{\tau _{xy}} = - \frac{{{\partial ^2}\varPhi }}{{\partial x\partial y}} $$ (12) 如图3所示，当浅梁分割为1/2厚时，由于浅梁不考虑层间挤压应力，即假定
$ {\sigma }_{y}= $ 0，符合浅梁中的柏努里假定[40]，上下面的梁仍然保持支撑在原点，则中性轴上的剪应力$\tau $ 为：![]()
图 3 浅梁分割应力分布Figure 3. Schematic diagrams showing the stress distributions in the slicing of a deep beam into shallow beams$$ \tau = \dfrac{{\dfrac{{ql}}{2}S}}{{bI}} = \dfrac{{ql\left( {b\dfrac{h}{2} \times \dfrac{h}{4}} \right)}}{{2b \dfrac{{b{h^3}}}{{12}}}} = \dfrac{3}{4}\times\dfrac{{ql}}{{bh}} $$ (13) 当梁沿中性轴分割后，上部浅梁将受到原荷载引起的弯矩ql2/4和反向弯矩ql2/8，同时还承受由中间水平剪应力引起的附加弯矩−3qlx/16，呈线性分布，另外需考虑跨中处由均布荷载产生的弯曲，并加上剪应力可得到梁的总弯矩为qlx/16，最后根据边界条件，求得梁的总挠度。当分割为1/4厚度时，同理进行总挠度计算。若继续分割下去，挠度与应力的分布也与分为两层厚的上半梁规律一致，和原梁保持相同的挠度。在计算深梁时，可沿跨度将其切分成若干“浅梁”，考虑均布荷载q以及考虑切开后σy对各“浅梁”扰度的影响，从而得到剪应力的分布。
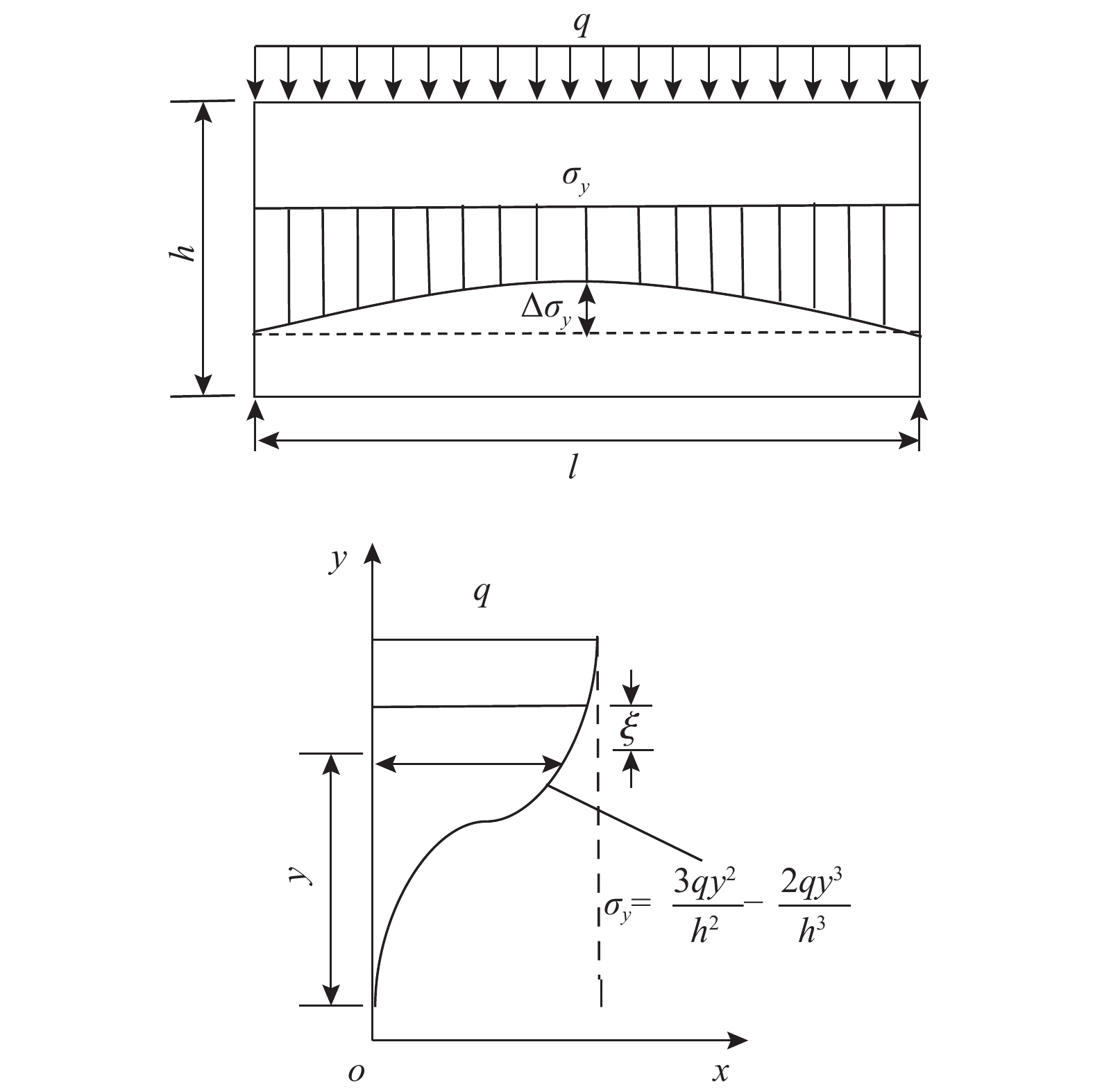
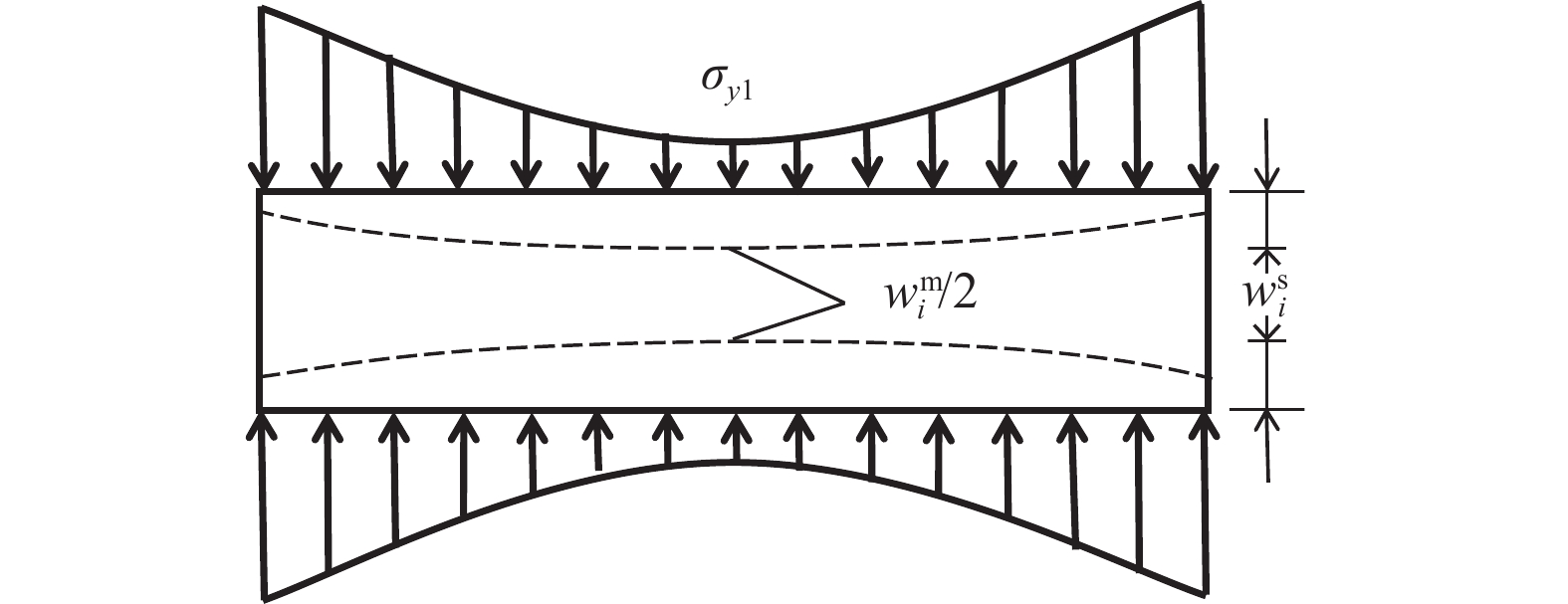
基于以上所述，切开后每一根“浅梁”上的荷载为σy，且由于最上面一根“浅梁”受到q作用影响，使分层后各个“浅梁”从上至下的弯矩逐渐增加。对于图4的梁，假设梁宽度为单位宽度，支座截面处为σy，且假定跨中与支座界面处差值∆σy按二次函数分布，先不考虑重力作用，则推导出：
$$\begin{aligned} & {\sigma _y}l + 2\int_0^{l/2} {a{x^2}{\mathrm{d}}x = ql} \\ & a = \frac{{12}}{{{l^2}}}\left( {q - {\sigma _y}} \right)\end{aligned} $$ (14) $$ 化简得： \Delta {\sigma _y} = a{x^2} - \frac{{12}}{{{l^2}}}\left( {q - {\sigma _y}} \right)\frac{{{l^2}}}{4} = 3\left( {q - {\sigma _y}} \right) $$ (15) 依据浅梁弹性力学解，可得均布荷载q引起的应力分量
$ {\sigma _y} = \dfrac{{3q{y^2}}}{{{h^2}}} - \dfrac{{2q{y^3}}}{{{h^3}}} $ 。由于σy引起的层间挤压应力的影响，在每一层切开的“浅梁”上、下表面上压缩变形的量不同，此时取平均值进行计算(图5)。
梁切开后在跨中处，上下表面的位移应是相等的，假设梁切开后的浅梁上表面的位移用wu表示，下表面位移用wl表示，上角标m表示跨中，上角标s表示端部，而弯曲引起的位移用wb表示，则w1u=w2l、w2u=w3l、w3u=w4l，以此类推，可得：
$$ \left\{ \begin{gathered} {w_{1{\mathrm{u}}}} = \frac{1}{2}w_1^{\mathrm{s}} + {w_{1{\mathrm{b}}}} + \frac{1}{2}w_1^{\mathrm{m}} \\ {w_{{\mathrm{2l}}}} = w_1^{\mathrm{s}} + \frac{1}{2}w_2^{\mathrm{s}} + {w_{2{\mathrm{b}}}} - \frac{1}{2}w_2^{\mathrm{m}} \\ {w_{2{\mathrm{u}}}} = w_1^{\mathrm{s}} + \frac{1}{2}w_2^{\mathrm{s}} + {w_{2{\mathrm{b}}}} + \frac{1}{2}w_2^{\mathrm{m}} \\ {w_{{\mathrm{3l}}}} = w_1^{\mathrm{s}} + w_2^{\mathrm{s}} + \frac{1}{2}w_3^{\mathrm{s}} + {w_{3{\mathrm{b}}}} - \frac{1}{2}w_3^{\mathrm{m}} \\ \qquad\qquad\qquad \vdots \\ \end{gathered} \right. $$ (16) 当
$ {w_{1{\mathrm{u}}}} = {w_{2{\mathrm{l}}}} $ 、$ {w_{2{\mathrm{u}}}} = {w_{3{\mathrm{l}}}} $ 、···、$ {w_{i{\mathrm{u}}}} = {w_{\left( {i + 1} \right){\mathrm{l}}}} $ 时，化简可得以下规律：$$ \left\{ \begin{gathered} {w_{1{\mathrm{b}}}} = {w_{_{2{\mathrm{b}}}}} + \frac{1}{2}\left[ {\left( {w_1^{\mathrm{s}} - w_1^{\mathrm{m}}} \right) + \left( {w_2^{\mathrm{s}} - w_2^{\mathrm{m}}} \right)} \right] \\ {w_{2{\mathrm{b}}}} = {w_{_{3{\mathrm{b}}}}} + \frac{1}{2}\left[ {\left( {w_2^{\mathrm{s}} - w_2^{\mathrm{m}}} \right) + \left( {w_3^{\mathrm{s}} - w_3^{\mathrm{m}}} \right)} \right] \\ \qquad\qquad\qquad\qquad \vdots \\ {w_{i{\mathrm{b}}}} = {w_{_{\left( {i + 1} \right){\mathrm{b}}}}} + \frac{1}{2}\left[ {\left( {w_i^{\mathrm{s}} - w_i^{\mathrm{m}}} \right) + \left( {w_{i + 1}^{\mathrm{s}} - w_{i + 1}^{\mathrm{m}}} \right)} \right] \\ \end{gathered} \right. $$ (17) 切开后“浅梁”上下表面的位移关系如下：
$$ {{w}}_i^{\mathrm{s}} - w_i^{\mathrm{m}} = \frac{{3q}}{E}\int_i {\left[ {1 - \left( {\frac{{3{y^{\text{2}}}}}{{{h^2}}} - \frac{{2{y^{\text{3}}}}}{{{h^3}}}} \right)} \right]} {\mathrm{d}}y $$ (18) 联立式(17)和式(18)，可推出：
$$ \begin{aligned} &{w_{i{\mathrm{b}}}} = {w_{\left( {i + 1} \right){\mathrm{b}}}} + \frac{{3q}}{{2E}}\left\{ \int_i {\left[ {1 - \left( {\frac{{3{y^2}}}{{{h^2}}} - \frac{{2{y^3}}}{{{h^3}}}} \right)} \right]} {\mathrm{d}}y +\right.\\ &\qquad \left.\int_{i + 1} {\left[ {1 - \left( {\frac{{3{y^2}}}{{{h^2}}} - \frac{{2{y^3}}}{{{h^3}}}} \right)} \right]} {\mathrm{d}}y \right\} \end{aligned}$$ (19) 通过上述公式所得结果，当把深梁条分成10层时，则第一层(i=1)为：
$$ \int_1 {\frac{{3{y^{\text{2}}}}}{{{h^2}}} - \frac{{2{y^{\text{3}}}}}{{{h^3}}}} {\mathrm{d}}y = \frac{1}{{{h^2}}}{y^3}|_0^{h/10} - \frac{1}{{{\text{2}}{h^3}}}{y^4}|_0^{h/10} = 0.009\;5\xi $$ (20) 同理，可得其余各层计算结果。联立式(20)和式(19)，可得弯矩引起的第一层和第二层的关系式：
$$ {w_{1{\mathrm{b}}}} = {w_{2{\mathrm{b}}}} + 2.892\frac{{q\xi }}{E} $$ (21) 同理，可得其余各层位移关系。可知，计算的弯曲位移如下：
$$ {w_{i{\mathrm{b}}}} = {\alpha _i}\frac{{{\sigma _{i - 1}} + \Delta {\sigma _{i - 1}} - {\sigma _i} - \Delta {\sigma _i}}}{{\xi E}}{l^2} $$ (22) 取ai为：
$$\left\{\begin{aligned} &{\alpha }_{1}=0.120，{\alpha }_{2}=0.118，{\alpha }_{3}=0.117，\\ &{\alpha }_{4}=0.115，{\alpha }_{5}=0.113，{\alpha }_{6}=0.112，\\ &{\alpha }_{7}=0.110，{\alpha }_{8}=0.108，{\alpha }_{9}=0.107，\\ &{\alpha }_{10}=0.105\end{aligned}\right. $$ (23) 当
$ {\alpha _i} $ 与$ {\alpha _{{\text{i}} + 1}} $ 之间取平均值计算，则$ \overline{{\alpha }_{1,2}}= \dfrac{{\alpha }_{1}+{\alpha }_{2}}{2}= 0.119 $ ，其余同理，式(22)和式(23)联立得：$$ \left\{ \begin{gathered} \frac{{{{{w}}_{{\text{1}}{\mathrm{b}}}}\xi E}}{{{\alpha _1}{l^2}}} = {\sigma _0} + \Delta {\sigma _0} - {\sigma _1} - \Delta {\sigma _1} \\ \frac{{{w_{{\text{2}}{\mathrm{b}}}}\xi E}}{{{\alpha _2}{l^2}}} = {\sigma _1} + \Delta {\sigma _1} - {\sigma _2} - \Delta {\sigma _2} \\ \end{gathered} \right. $$ (24) 由
$ {\sigma _{i - 1}} - {\sigma _i} = {\sigma _i} - {\sigma _{i + 1}} $ ，将式(24)相减得：$$ \Delta {\sigma _0} - 2\Delta {\sigma _1} + \Delta {\sigma _2} = \frac{{\left( {{w_{1{\mathrm{b}}}} - {w_{2{\mathrm{b}}}}} \right)\xi E}}{{\overline \alpha {l^2}}} $$ (25) 根据各层位移关系，将式(21)、
$ \xi = \dfrac{h}{{10}} $ 代入式(25)化简得：$$ \left\{\begin{aligned} &\Delta {\sigma }_{0}-2\Delta {\sigma }_{1}+\Delta {\sigma }_{2}=\frac{2.892}{\overline{{\alpha }_{1,2}}}\times \frac{q{\xi }^{2}}{{l}^{2}}=0.243q{\left(\frac{h}{l}\right)}^{2}\\ &\Delta {\sigma }_{1}-2\Delta {\sigma }_{2}+\Delta {\sigma }_{3}=\frac{2.670}{\overline{{\alpha }_{2,3}}}\times \frac{q{\xi }^{2}}{{l}^{2}}=0.227q{\left(\frac{h}{l}\right)}^{2}\\ &\qquad\qquad\qquad\qquad\qquad \vdots\\ &\Delta {\sigma }_{8}-2\Delta {\sigma }_{9}+\Delta {\sigma }_{10}=\frac{0.108}{\overline{{\alpha }_{9,10}}}\times \frac{q{\xi }^{2}}{{l}^{2}}=0.010\;2q{\left(\frac{h}{l}\right)}^{2}\end{aligned}\right. $$ (26) 当对∆σ的弯矩进行平衡时，则∑M=0，则：
$$ \begin{aligned} & 0.167\Delta {\sigma _0} + \Delta {\sigma _1} + 2\Delta {\sigma _2} + 3\Delta {\sigma _3} + 4\Delta {\sigma _4} + 5\Delta {\sigma _5} + \\ &\qquad 6\Delta {\sigma _6} + \Delta {\sigma _7} + 8\Delta {\sigma _8} + 9\Delta {\sigma _9} + 4.833\Delta {\sigma _{10}} = 0 \end{aligned} $$ (27) 当∑X=0时：
$$ \begin{aligned} & \Delta {\sigma _0} + 2\left( {\Delta {\sigma _1} + \Delta {\sigma _2} + \Delta {\sigma _3} + \Delta {\sigma _4} + \Delta {\sigma _5}} \right. + \\ &\qquad \Delta {\sigma _6} + \Delta {\sigma _7} + \Delta {\sigma _8} + \left. {\Delta {\sigma _9}} \right) + \Delta {\sigma _{10}} = 0 \end{aligned} $$ (28) 将式(26)—式(28)联立，得到方程组，利用Matlab进行计算，得：
$$ \left.\begin{aligned} &\Delta {\sigma }_{0}=1.336\;4、\Delta {\sigma }_{1}=0.511\;4、\\ &\qquad \Delta {\sigma }_{2}=-0.070\;6\\ &\Delta {\sigma }_{3}=-0.425\;3、\Delta {\sigma }_{4}=-0.578\;4、\\ &\qquad \Delta {\sigma }_{5}=-0.561\;5\\ &\Delta {\sigma }_{6}=-0.411\;2、\Delta {\sigma }_{7}=-0.165\;3、\\ &\qquad \Delta {\sigma }_{8}=0.141\;2\\ &\Delta {\sigma }_{9}=0.478\;5、\Delta {\sigma }_{10}=0.825\;9\end{aligned}\right\}q{\left(\frac{h}{l}\right)}^{2} $$ (29) $$\left.\begin{aligned} &{\sigma }_{0}=1.92、{\sigma }_{1}=1.02、{\sigma }_{2}=0.37\\ &{\sigma }_{3}=-0.097、{\sigma }_{4}=-0.36、{\sigma }_{5}=-0.45\\ &{\sigma }_{6}=-0.41、{\sigma }_{7}=-0.36、{\sigma }_{8}=-0.31\\ &{\sigma }_{9}=-0.25、{\sigma }_{10}=-0.19\end{aligned}\right\}q{\left(\frac{h}{l}\right)}^{2} $$ (30) 已知材料力学中剪应力公式[40]为：
$$ \frac{{{Q_{{x}}}S}}{I} = {\tau _{xy}} $$ (31) 当均布荷载时，弯矩按二次抛物线分布，结合弹性力学公式，化简后得：
$$ {\tau _{{{xy}}}} = \frac{{{\mathrm{d}}{M_x}}}{{{\mathrm{d}}x}}\frac{S}{I} = {M_0}\frac{S}{I}\left( {\frac{8}{{{l^2}}}} \right) = \Delta F\left( {\frac{8}{{{l^2}}}} \right) $$ (32) 根据式(32)，对∆F进行求解，再对τ进行计算，当计算第一层剪应力时：
$$ \Delta {F_{01}} = \frac{{1.92 + 1.02}}{2} \times q\frac{h}{{10}} = 0.147qh $$ (33) $$ {\tau _1} = \Delta F\frac{8}{{{h^2}}}x = 0.147qh \times \frac{8}{{{h^2}}}x = 1.176q\frac{x}{h} $$ (34) $$ \Delta {F_{12}} = \frac{{1.02 + 0.37}}{2} \times q\frac{h}{{10}} = 0.069\;5qh $$ (35) 则第二层剪应力为：
$$ {\tau _2} = {\tau _1} + \Delta {F_{12}}\frac{8}{{{h^2}}}x = 1.732q\frac{x}{h} $$ (36) 同理进行其余各层剪应力计算，不再赘述。
2.3 精度评价
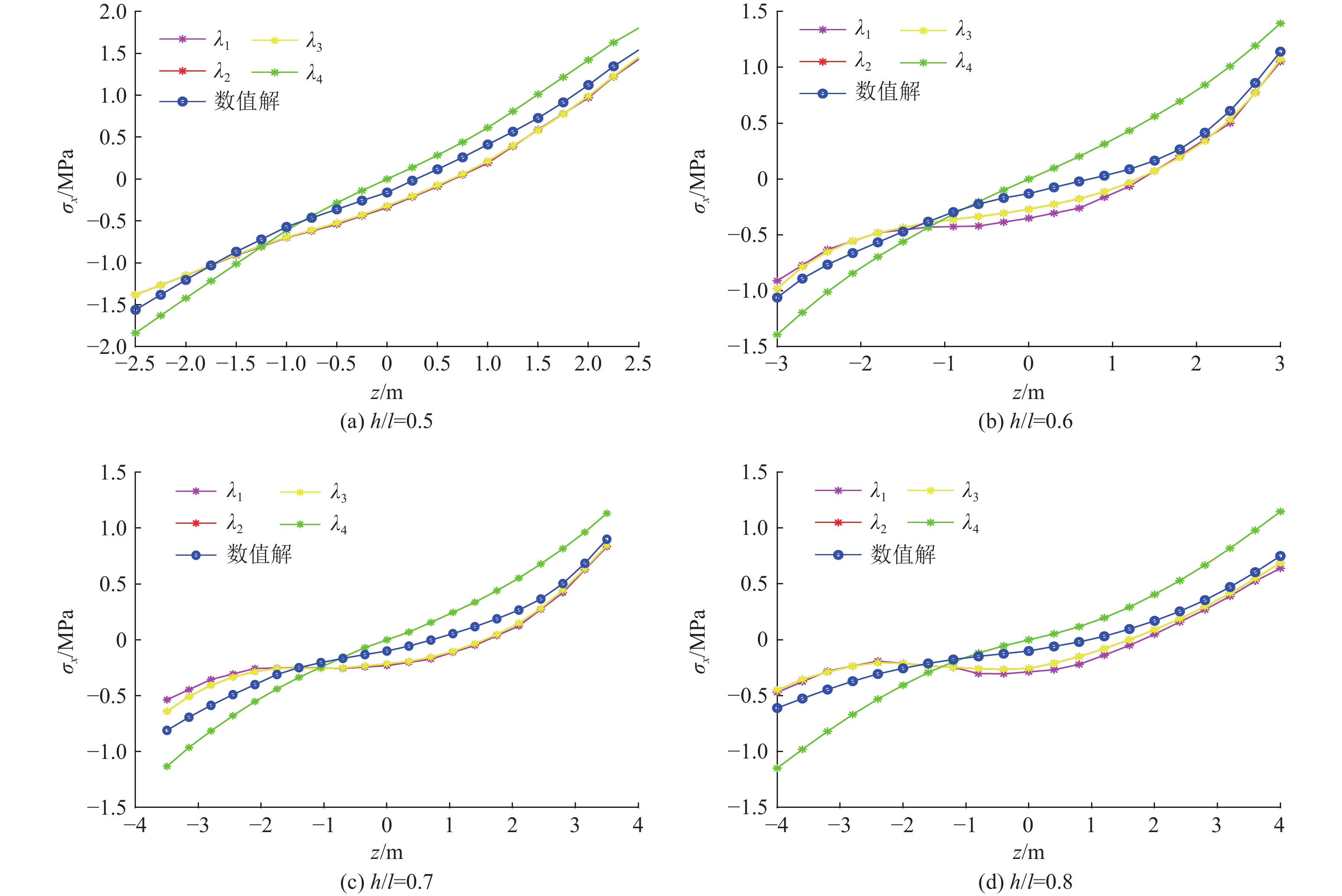
为探讨深梁条分解精度以及条分层数对深梁条分解析解影响，将其与常规弹性力学解、FLAC3D数值解进行对比，以两解法偏离数值解大小的值视为相对误差，分析应力计算结果与条分层数及高跨比的关系，揭示条分法精度变化规律。取λ1—λ3分别为条分为10、16、20层时的深梁力学解，弹性力学解为λ4。梁跨度(即初次来压步距)l为10 m，梁高h分别为5、6、7、8 m，即高跨比h/l为0.5、0.6、0.7、0.8，梁上受均布荷载q=0.5 MPa，泊松比为0.25(图6)。
通过对比图6，可以看出两种解析解在模型跨中位置处应力随z轴坐标的变化趋势基本相同。随着高跨比的不断增加，弹性力学解的中性轴仍在中间位置处，应力误差逐渐增大，是由于弹性力学解未考虑层间挤压应力σy的影响。深梁在荷载作用下，内部应力会发生重分布，层间挤压应力越向下越向支座处集中，剪应力相应集中，中性轴不在中间，将会向下偏移。而深梁条分解与数值解总体趋势一致，中性轴位置逐渐发生变化，呈向下移动趋势。3种分层层数随着高跨比增加也产生了相应误差。
从表1可以看出其精度误差从13.3%增加到53.3%，这是由于弹性力学解在应用应力函数和协调方程求解时将层间挤压应力σy当成0处理，而随着开采深度增加，围岩应力较为复杂，深梁需考虑剪切作用的影响，因此该方法下的弹性力学解适合浅梁。同时，从表1可以看出，随着条分层数增加，条分解精度也在增加，但提高幅度逐渐降低，因此，工程应用中针对深部岩梁模型条分到一定程度即可，且随着高跨比不断增加，精度误差也在增加，说明条分层宽度不宜过大，否则造成误差增加。
表 1 解析解与数值解正应力对比分析Table 1. Comparative analysis of normal stress obtained using analytical and numerical methodsh/l 数值法正应力解/MPa 深梁条分解法 弹性力学法 层数 正应力解/MPa 相对误差/% 正应力解/MPa 相对误差/% 0.5 1.58 10 1.470 6.69 1.79 13.3 16 1.491 5.63 20 1.490 5.69 0.6 1.14 10 1.056 7.32 1.35 18.4 16 1.069 6.23 20 1.070 6.14 0.7 0.91 10 0.834 7.98 1.23 35.2 16 0.846 7.13 20 0.849 6.70 0.8 0.75 10 0.687 8.32 1.15 53.3 16 0.691 7.87 20 0.694 7.50 3 工程案例分析
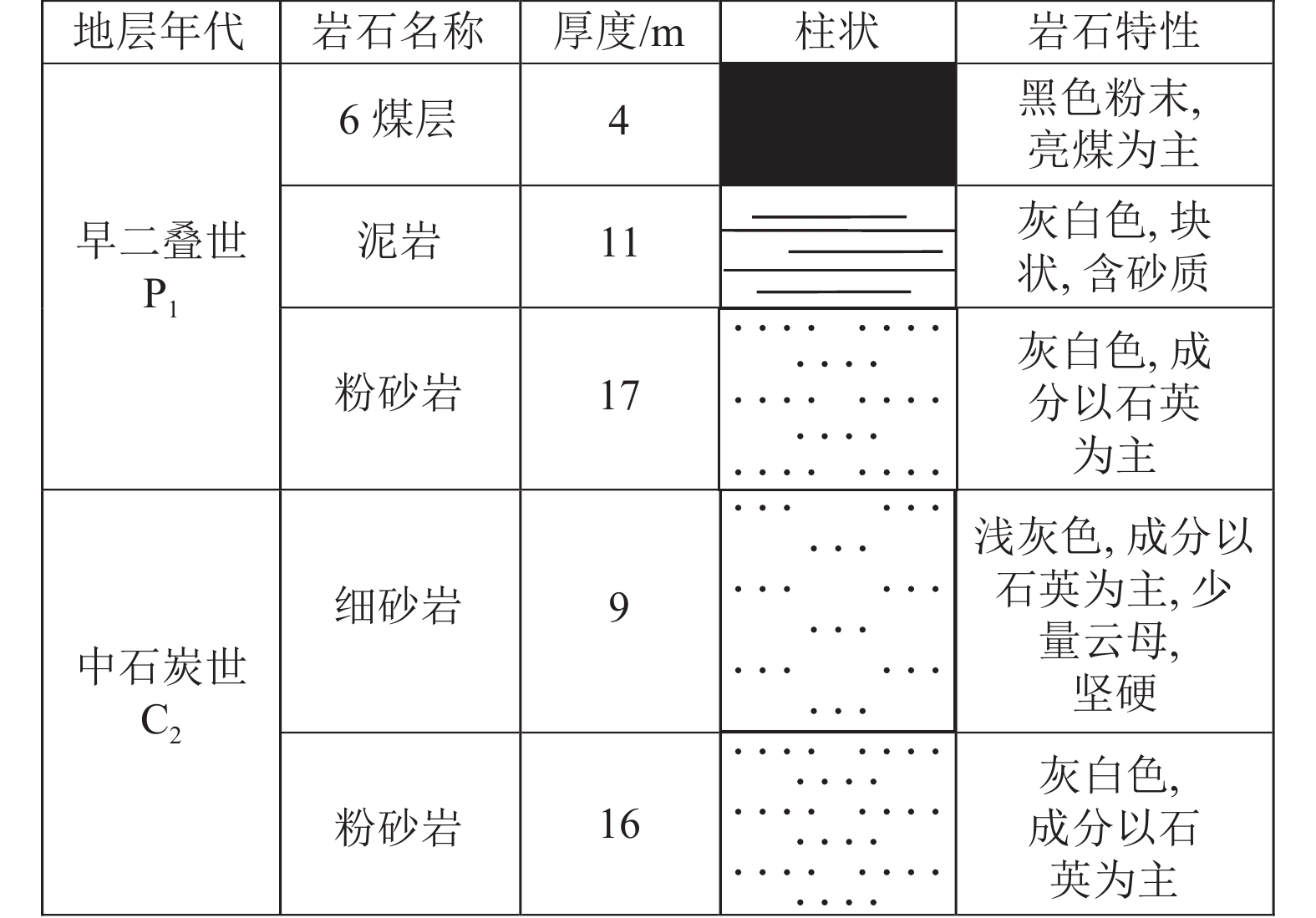
皖北煤电集团某采煤工作面平均埋深850 m，主采6煤层，煤层平均倾角12.5°，视为近水平煤层，6煤层下伏53 m为太原组灰岩含水层，即隔水层总厚为53 m。工作面倾向宽为180 m，走向长722 m，距工作面下部30 m为太原组灰岩含水层，该含水层富水性较强，对工作面的安全回采具有较大影响。由矿压资料可知，底板最大水压p=2.54 MPa。底板采动破坏深度h1=20 m，位于底板细砂岩顶面。工作面初次来压步距为15 m，上覆岩层平均容重γ=27 kN/m3，弹性模量为18 GPa，泊松比为0.25，采用疏水降压及局部注浆方式进行水害治理，隔水底板承受最大水压为6 MPa，根据关键层判别原则[41]，9 m厚的细砂岩可视为底板隔水关键层，岩性柱状如图7所示。
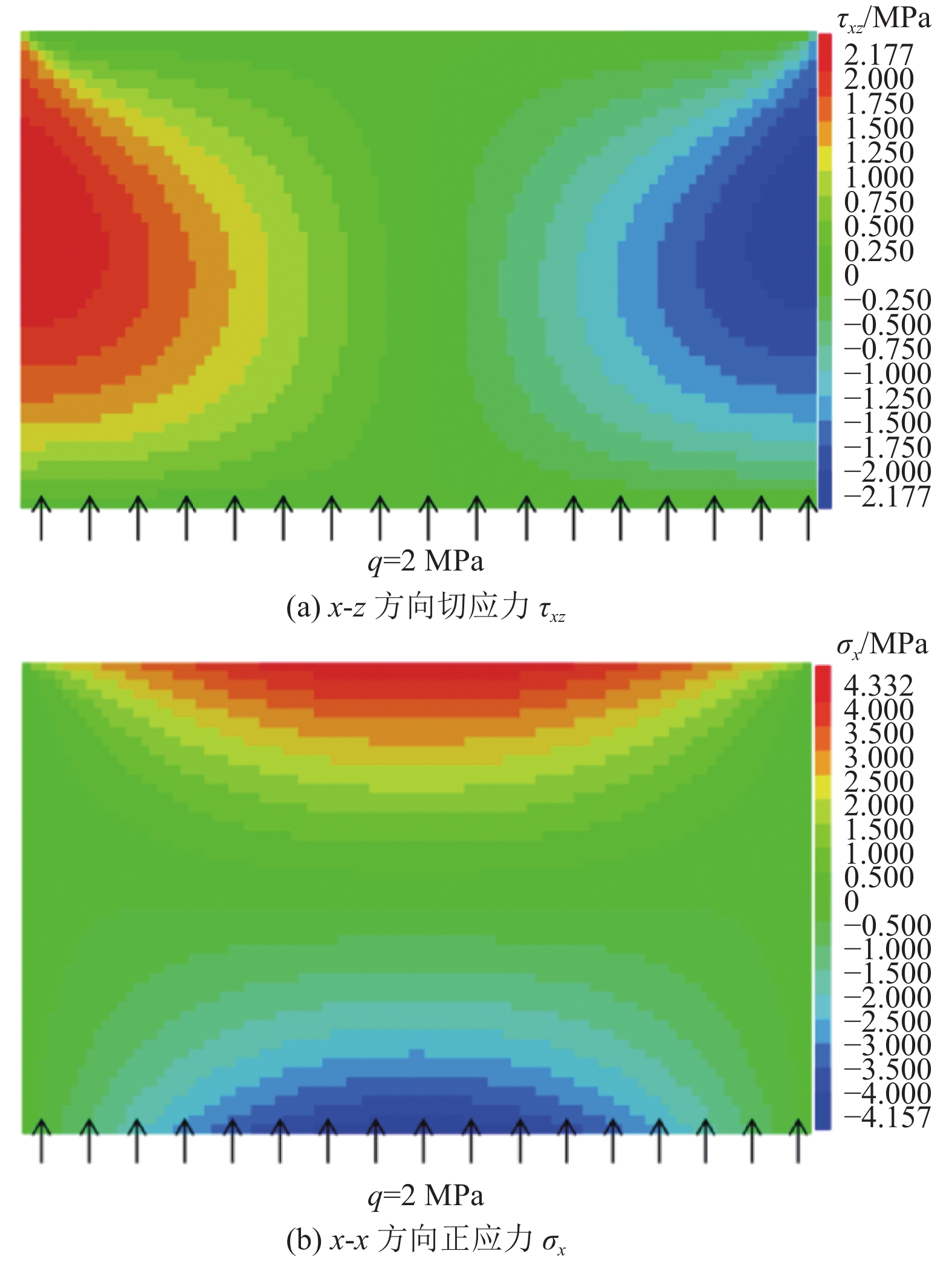
将关键层从红色区域取出，在工作面推进方向取单位宽度简化为平面应变问题，进行如图8所示数值模拟。根据FLAC3D软件坐标特点，设y方向为平面应变方向，z轴为竖直方向，x轴方向为关键层跨度方向，关键层底部施加均布荷载q。根据关键层简支梁特点，y方向位移全约束，端部固定z方向位移，为了减小计算误差，网格划分为100×100。模型中关键层的物理力学参数见表2。
![]()
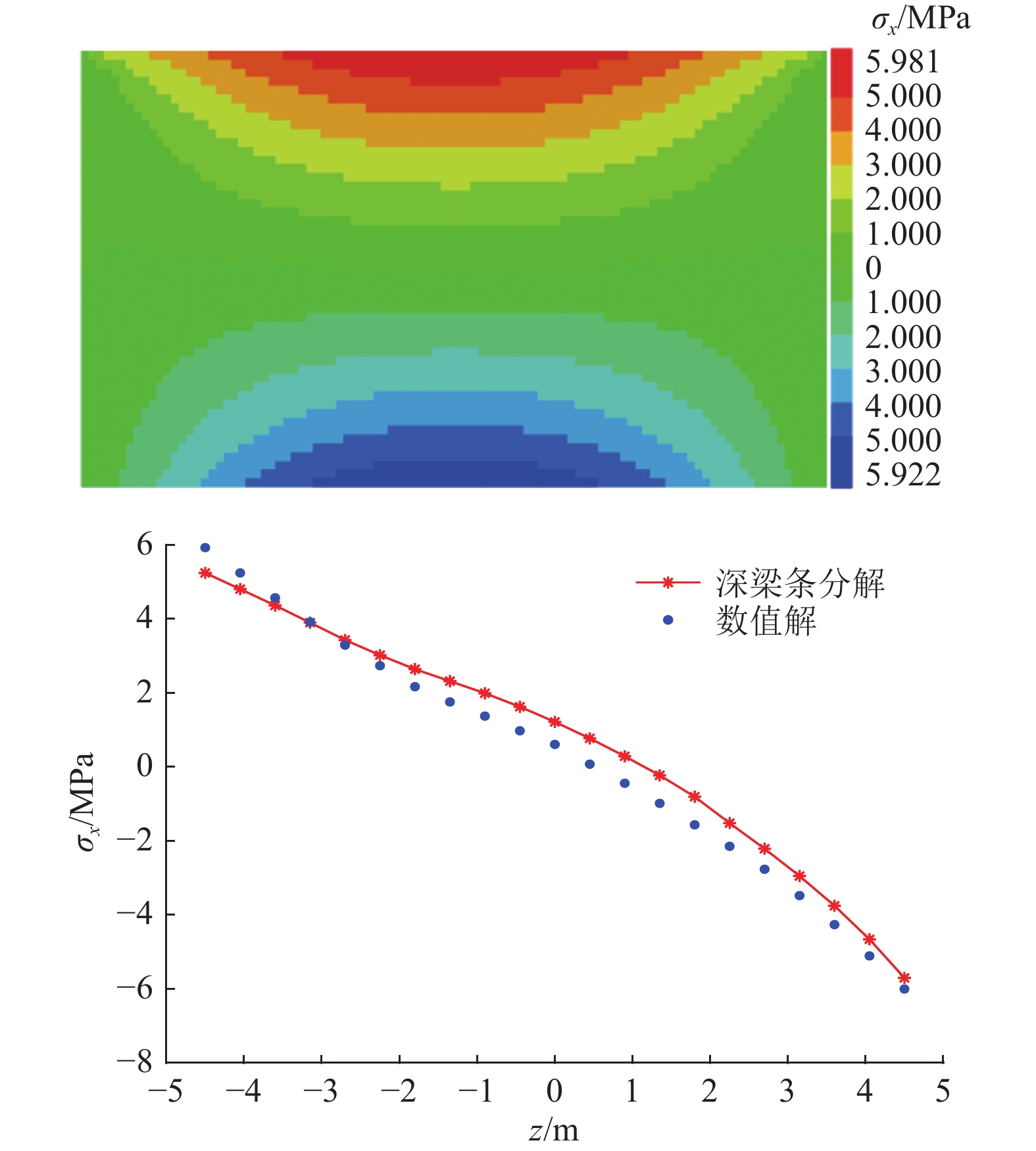
图 8 工作面隔水关键层数值模拟Figure 8. Numerical simulation of a water-resisting key stratum on the mining face表 2 岩层物理力学计算指标Table 2. Physical and mechanical calculation indices of rock layers岩石名称 层厚/m 密度/(kg·m–3) 弹性模量/GPa 泊松比 细砂岩 9 2 600 18 0.25 利用FLAC3D数值软件的模拟，得到隔水关键层应力矢量分布(图9，正值表示拉应力，负值表示压应力，其他同)。图9a可看出关键层切应力τxz左边和右边分别为2.17和−2.09 MPa，应力中间处无太多变化，两端应力向下方逐渐增大；从图9b可看出关键层正应力σx从−4.15 MPa增加到4.33 MPa，呈逐渐增大的趋势，而左右两端应力值未发生太大变化，在水压力作用下，底板关键层产生向上弯曲，上部受拉，下部受压，跨中界面上部处拉应力最大，因此判定底板突水的关键点应该关注拉应力最大处。
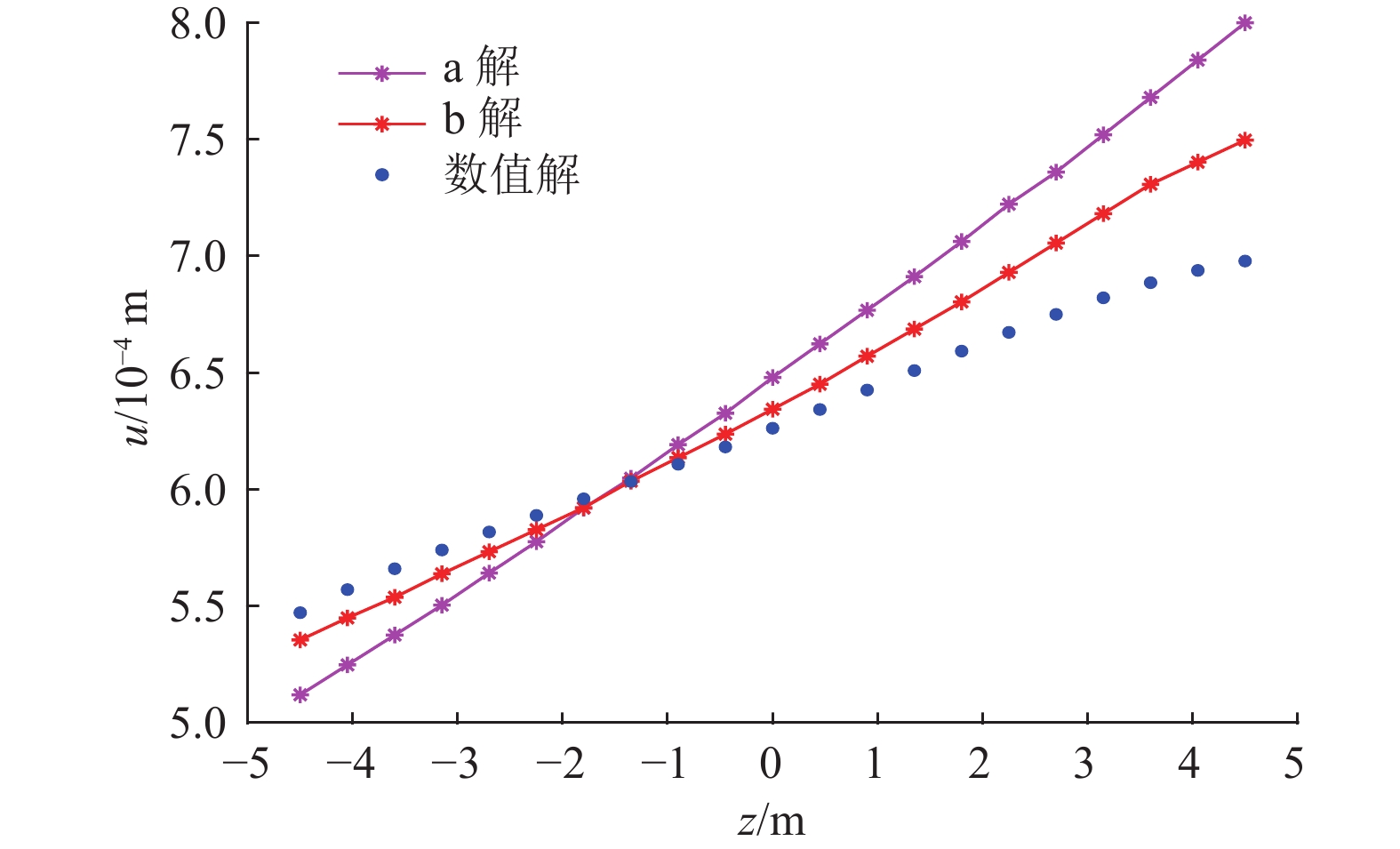
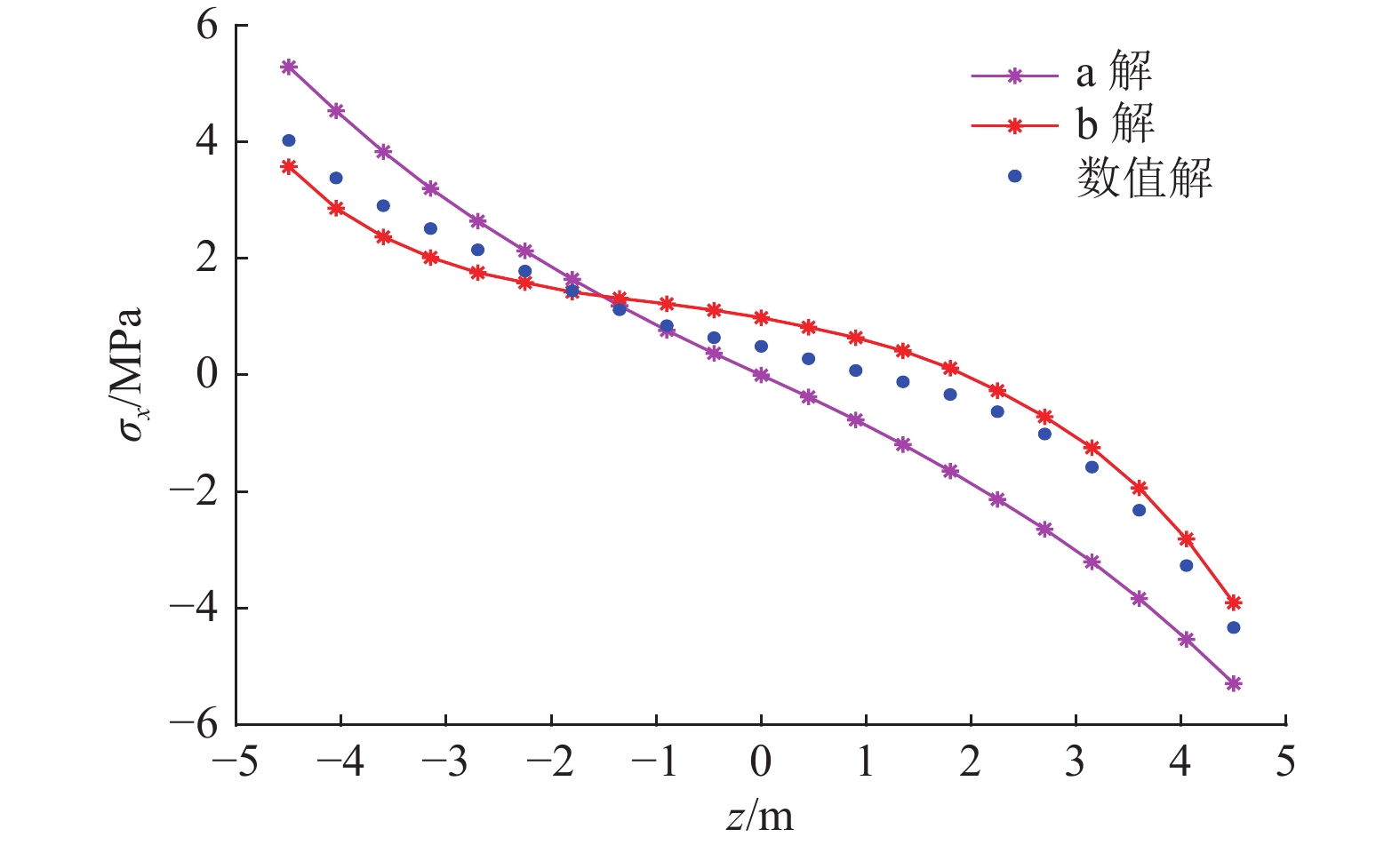
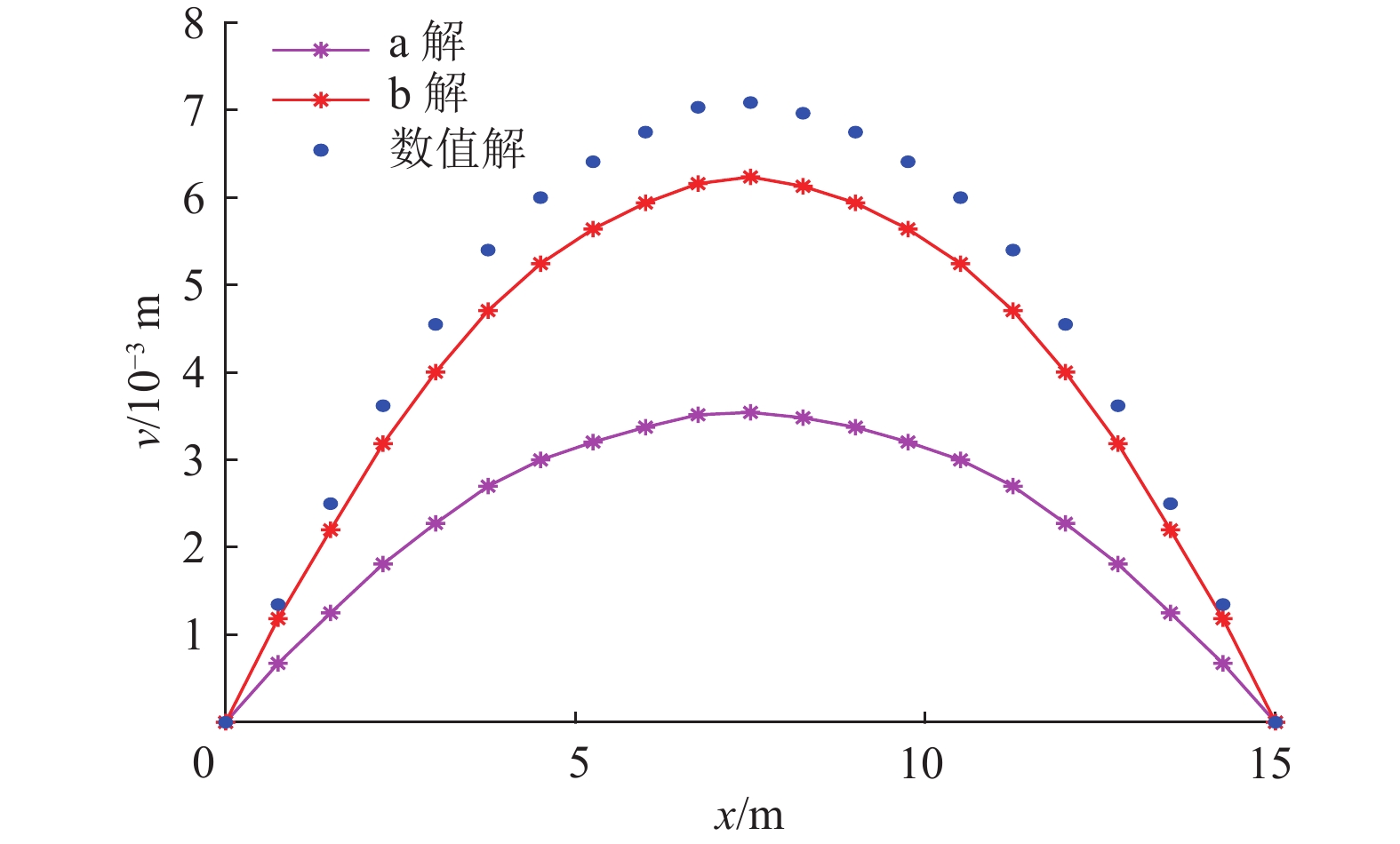
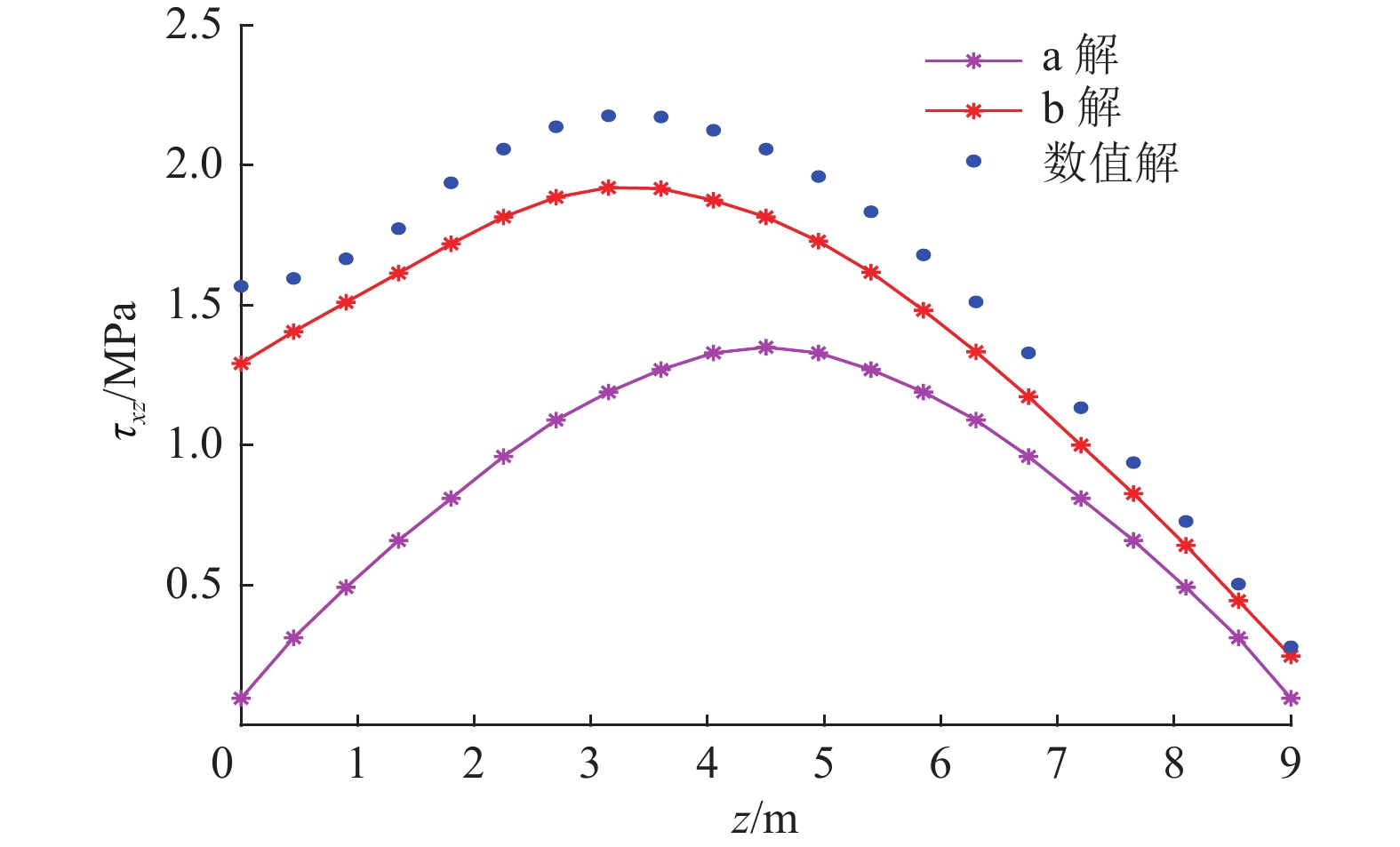
建立如图10所示简支深梁力学模型，由上述工作面资料可得，hk=9 m，l=15 m，高跨比h/l=0.6，为深梁情况。根据煤层数据资料计算可得q=2 MPa。将隔水关键层深梁模型分为20层进行求解，此时分层厚度为0.45 m。为探讨深梁条分解的精确性及有效性，通过Matlab软件对两种解法的应力结果计算成图，与FLAC3D数值解对比成图，其中弹性力学解定为a解，深梁条分解定为b解，如图11—图14所示，并利用深梁条分解对工作面底板突水危险性进行分析。
分析图11，各解析解在跨中x=7.5 m时随着z轴水平位移变化趋势中，条分解与数值解较为接近，数值解、a解和b解的最大水平位移分别为0.068、0.080和0.074 cm，与数值解的相对误差分别为17.60%和8.82%，深梁条分解理论值更为精确。
分析图12，可得到各解析解的垂直位移随着x轴坐标的变化趋势，看出条分解与数值解较为接近；简支梁由于其两端边界条件，垂直方向不发生位移，中间处呈“抛物线”趋势，数值解的最大垂直位移是0.71 cm；a解理论值的最大垂直位移是0.43 cm，相对误差约39.4%；b解理论值的最大垂直位移是0.63 cm，相对误差约10.2%。
分析图13，取模型1/3段即x在0~5 m时，剪应力随着z轴坐标的变化趋势，看出条分解与数值解较为接近，得知弹性力学剪应力最大处在z轴中间即板中间处，即中性轴在中间位置处，呈对称分布；而σy越向下越向支座集中，剪应力也相应地集中，中性轴会发生位移，应力趋势非线性分布；数值解、a解理论值和b解理论值的最大拉应力分别为2.17、1.29和1.94 MPa，后两者与数值解的相对误差分别为40.6%和10.5%。
分析图14，可得出处于模型的跨中位置时，正应力随着z轴坐标的变化呈下移趋势，符合深梁内力特性；数值解、a解理论值和b解理论值的最大拉应力分别为4.33、5.28和3.91 MPa，后两者与数值解的相对误差分别为18.00%和9.69%。
由图15可得，当工作面推进至18 m处，即高跨比为0.5时，数值解的最大拉应力为5.98 MPa，即将达到工作面隔水层底板最大抗拉强度临界值，有发生突水危险可能性，深梁条分解理论值的最大拉应力为5.65 MPa，相对误差为5.51%，在工程误差精度范围内。
![]()
图 15 x=18 m时隔水关键层跨中应力矢量图及对比分析Figure 15. Vector diagram and comparative analysis of mid-span stress in the key aquiclude under x = 18 m通过以上应力及位移数据分析，深梁条分解与数值解趋势更为贴近，相对误差在10%左右，而弹性力学解相对误差最大达到40.6%，对于深梁情况下的力学分析已然不够精确，在实际工程应用深梁情况中，此条分解更为精确，优先采用。根据皖北煤矿工作面开采实例可得，底板隔水关键层最大拉应力为6 MPa，当工作面推荐进18 m时，利用深梁条分解计算达到关键层的抗拉强度临界值，关键层有突水失稳的可能性，会造成关键层拉断引发突水事故，目前采煤工作面正常。
4 结 论
(1)分别通过弹性力学解、深梁条分解两种解析解计算均布荷载水压力下的关键层应力和位移，发现深梁条分解与数值解相差不大，其结果更为精确，表明本方法有效可靠。
(2)随着高跨比增加，条分解解出的深梁中性轴位置与数值解基本吻合，存在着不同程度的偏移，而弹性力学求解出的中性轴维持在中间不变，与深梁实际应力特点不符合，该方法下的弹性力学解适合浅梁。
(3)随着条分层数增加，精度也在增加，但提高幅度逐渐降低，因此，工程应用中针对深部岩梁模型条分到一定程度即可，且随着高跨比不断增加，精度误差也在增加，说明条分层宽度不宜过大，否则造成误差增加。
(4)底板隔水关键层实例表明，当隔水关键层高跨比大于0.2时，为典型的深梁问题，常规弹性力学的最大拉应力求解结果误差较大，给正确判定关键层突水危险性带来不利影响，此时采用深梁条分法求解应力精度较高，可为底板突水的预测情况起到较好的指导作用。
符号注释：
a为表示力分布的常数；b为煤层底板宽度，取单位宽度1；A、B、C、D、H、K为应力函数中待定系数；E为弹性模量，GPa；f2(x)为应力函数中待求函数；∆F为跨中截面处剪切力，kN；∆F01、∆F12分别为深梁分层后(从上往下数)第一层、第二层浅梁截面处的剪切力，kN；h为梁高度，m；h1为采动破坏带最大高度，m；h2为完整隔水层带最大高度，m；h2’为底板采动破坏带高度，m；h3为承压水导升带最大高度，m；hk为关键层厚度，m；i为深梁分层数；I为梁横截面的惯性矩，m4；l为初次来压步距，m；M为弯矩，kN·m；M0为跨中处弯矩，kN·m；Mx为梁任意x截面处弯矩，kN·m；p为底板所受均布水压力，MPa；Qx为梁任意x截面处剪切力，kN；q为简支梁受到均布荷载，kN/m²；S为梁横截面切应力对中性轴的静矩，m3；u、v为位移分量，m；u0、v0为某点在水平方向与竖直的位移，两者均为积分常数，m；
$ w $ ib、$ w $ il、$ w $ iu(i=1，2，3，···)分别为深梁条分i层浅梁时，第i层浅梁(从上往下数)弯曲引起、上表面和下表面的位移，m；$ {w}_{i}^{\mathrm{m}} $ 、$ {w}_{i}^{\mathrm{s}} $ (i=1，2，3，···)分别为深梁条分i层浅梁时，第i层浅梁(从上往下数)跨中处和端部处的位移，m；$ {\alpha }_{i} $ (i=1，2，3，…)为深梁条分i层浅梁时，第i层浅梁弯曲引起位移系数；$\bar \alpha $ 为位移系数平均值；$ \overline{{\alpha }_{i,i+1}} $ 为相邻两层浅梁弯曲引起位移系数的平均值，$ \overline{{\alpha }_{i,i+1}} $ =$ \left({\alpha }_{i}+{\alpha }_{i+1}\right)/2 $ ；γ为底板平均容重，kN/m3；σ0为深梁切开分成浅梁后第一层上表面的正应力，MPa；∆σ0为深梁切开分成浅梁后第一层上表面的正应力差值，MPa；$ {\sigma }_{i} $ (i=1，2，3，···)为第i层浅梁x方向的正应力，MPa；$ {\sigma }_{x} $ 、$ {\sigma }_{y} $ 分别为关键层x方向正应力和y方向层间挤压应力，MPa；∆σy、∆σi分别为支座处$ {\sigma }_{y} $ 和$ {\sigma }_{x} $ 与跨中处差值，MPa；σy1为切开后第一层层间挤压应力，MPa；μ为泊松比；$\xi $ 为积分常数；τ1、τ2分别为切开后第一层、第二层剪应力，MPa；$ {\tau }_{xy}、{\tau }_{x{\textit{z}}}\mathrm{分}\mathrm{别} $ 为xy、xz方向剪应力，MPa；$ \varphi (x,y) $ 为应力函数中待求函数；$ \varPhi $ 为应力函数；$ \omega $ 为梁某点的转动位移，是积分常数；$\nabla $ 为梯度算子。 -
![]()
图 2 2种解法下隔水关键层简支梁力学模型
Fig. 2 Mechanical model of a simply supported beam for a key aquiclude under two solutions
![]()
图 3 浅梁分割应力分布
Fig. 3 Schematic diagrams showing the stress distributions in the slicing of a deep beam into shallow beams
![]()
图 8 工作面隔水关键层数值模拟
Fig. 8 Numerical simulation of a water-resisting key stratum on the mining face
![]()
图 15 x=18 m时隔水关键层跨中应力矢量图及对比分析
Fig. 15 Vector diagram and comparative analysis of mid-span stress in the key aquiclude under x = 18 m
表 1 解析解与数值解正应力对比分析
Table 1 Comparative analysis of normal stress obtained using analytical and numerical methods
h/l 数值法正应力解/MPa 深梁条分解法 弹性力学法 层数 正应力解/MPa 相对误差/% 正应力解/MPa 相对误差/% 0.5 1.58 10 1.470 6.69 1.79 13.3 16 1.491 5.63 20 1.490 5.69 0.6 1.14 10 1.056 7.32 1.35 18.4 16 1.069 6.23 20 1.070 6.14 0.7 0.91 10 0.834 7.98 1.23 35.2 16 0.846 7.13 20 0.849 6.70 0.8 0.75 10 0.687 8.32 1.15 53.3 16 0.691 7.87 20 0.694 7.50 
下载: 导出CSV
表 2 岩层物理力学计算指标
Table 2 Physical and mechanical calculation indices of rock layers
岩石名称 层厚/m 密度/(kg·m–3) 弹性模量/GPa 泊松比 细砂岩 9 2 600 18 0.25
下载: 导出CSV
-
[1] 袁亮. 我国煤炭主体能源安全高质量发展的理论技术思考[J]. 中国科学院院刊,2023,38(1):11−22. YUAN Liang. Theory and technology considerations on high-quality development of coal main energy security in China[J]. Bulletin of Chinese Academy of Sciences,2023,38(1):11−22.
[2] 孙文洁,李文杰,宁殿艳,等. 我国煤矿水害事故现状、预测及防治建议[J]. 煤田地质与勘探,2023,51(12):185−194. DOI: 10.12363/issn.1001-1986.23.05.0273 SUN Wenjie,LI Wenjie,NING Dianyan,et al. Current states,prediction and prevention suggestions for water hazard accidents in China’s coal mines[J]. Coal Geology & Exploration,2023,51(12):185−194. DOI: 10.12363/issn.1001-1986.23.05.0273
[3] 何满潮,谢和平,彭苏萍,等. 深部开采岩体力学研究[J]. 岩石力学与工程学报,2005,24(16):2803−2813. DOI: 10.3321/j.issn:1000-6915.2005.16.001 HE Manchao,XIE Heping,PENG Suping,et al. Study on rock mechanics in deep mining engineering[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2803−2813. DOI: 10.3321/j.issn:1000-6915.2005.16.001
[4] 谢和平. “深部岩体力学与开采理论” 研究构想与预期成果展望[J]. 工程科学与技术,2017,49(2):1−16. XIE Heping. Research framework and anticipated results of deep rock mechanics and mining theory[J]. Advanced Engineering Sciences,2017,49(2):1−16.
[5] 李强. 煤层底板隔水关键层失稳及突水危险性研究[D]. 青岛:山东科技大学,2019. LI Qiang. Study on coal seam floor water resisting key strata instability and water inrush risk[D]. Qingdao:Shandong University of Science and Technology,2019.
[6] 郑士田,马荷雯,姬亚东. 煤层底板水害区域超前治理技术优化及其应用[J]. 煤田地质与勘探,2021,49(5):167−173. ZHENG Shitian,MA Hewen,JI Yadong. Optimization of regional advanced coal floor water hazard prevention and control technology and its application[J]. Coal Geology & Exploration,2021,49(5):167−173.
[7] 王素玲,娄富林. 深部煤层开采数值模拟与底板突水预测[J]. 煤炭技术,2020,39(5):122−125. WANG Suling,LOU Fulin. Numerical simulation of deep coal seam mining and prediction of water inrush from floor[J]. Coal Technology,2020,39(5):122−125.
[8] 尹尚先,王屹,尹慧超,等. 深部底板奥灰薄灰突水机理及全时空防治技术[J]. 煤炭学报,2020,45(5):1855−1864. YIN Shangxian,WANG Yi,YIN Huichao,et al. Mechanism and full-time-space prevention and control technology of water inrush from Ordovician and thin limestone in deep mines[J]. Journal of China Coal Society,2020,45(5):1855−1864.
[9] 范胜洋. 采动底板突水孕灾演化规律研究[D]. 徐州:中国矿业大学,2020. FAN Shengyang. Study on the evolution law of water inrush from mining floor[D]. Xuzhou:China University of Mining and Technology,2020.
[10] 钱鸣高,缪协兴,许家林,等. 岩层控制的关键层理论[M]. 徐州:中国矿业大学出版社,2000:199–218. [11] 孙建,王连国,鲁海峰. 基于隔水关键层理论的倾斜煤层底板突水危险区域分析[J]. 采矿与安全工程学报,2017,34(4):655−662. SUN Jian,WANG Lianguo,LU Haifeng. The analysis of the water-inrush dangerous areas in the inclined coal seam floor based on the theory of water-resisting key strata[J]. Journal of Mining & Safety Engineering,2017,34(4):655−662.
[12] 鲁海峰,孟祥帅,张元,等. 采场底板层状结构关键层隔水性能力学分析[J]. 中国矿业大学学报,2020,49(6):1057−1066. LU Haifeng,MENG Xiangshuai,ZHANG Yuan,et al. Mechanical analysis of water barrier performance of floor layered structure key stratum on coal face[J]. Journal of China University of Mining & Technology,2020,49(6):1057−1066.
[13] 冯梅梅,茅献彪,朱庆华. 底板隔水层岩性组合特征对隔水性能的影响[J]. 采矿与安全工程学报,2010,27(3):404−409. DOI: 10.3969/j.issn.1673-3363.2010.03.021 FENG Meimei,MAO Xianbiao,ZHU Qinghua. Effect of lithologic association of the water-resisting strata in coal seam floor on water insulating[J]. Journal of Mining & Safety Engineering,2010,27(3):404−409. DOI: 10.3969/j.issn.1673-3363.2010.03.021
[14] 孙强,刘恒凤,张吉雄,等. 充填开采隔水关键层渗流稳定性力学模型及分析[J]. 采矿与安全工程学报,2022,39(2):273−281. SUN Qiang,LIU Hengfeng,ZHANG Jixiong,et al. Mechanical model and analysis of seepage stability in key aquiclude strata during backfill mining[J]. Journal of Mining & Safety Engineering,2022,39(2):273−281.
[15] 阮浩. 基于欧拉梁理论的风电叶片疲劳试验弯矩匹配优化方法研究[D]. 重庆:重庆理工大学,2023. RUAN Hao. Research on optimization method of bending moment matching in fatigue test of wind turbine blades based on Euler beam theory[D]. Chongqing:Chongqing University of Technology,2023.
[16] 谢丹,黄勇刚. 大挠度欧拉梁三参数曲率模型及其在平面柔顺机构中的应用[J]. 机械工程学报,2021,57(13):144−152. DOI: 10.3901/JME.2021.13.144 XIE Dan,HUANG Yonggang. Novel model with three curvature variables for Euler beam under large deflection and its application in planar compliant mechanisms[J]. Journal of Mechanical Engineering,2021,57(13):144−152. DOI: 10.3901/JME.2021.13.144
[17] 祝卫亮,葛耀君. 悬索桥桁架加劲梁动力等效成等截面欧拉梁方法[J]. 哈尔滨工业大学学报,2020,52(9):17−24. DOI: 10.11918/201906080 ZHU Weiliang,GE Yaojun. Simplified method for dynamic equivalent Euler beam of truss girder in suspension bridge[J]. Journal of Harbin Institute of Technology,2020,52(9):17−24. DOI: 10.11918/201906080
[18] 余阳,杨洋. 基于非局部应变梯度欧拉梁模型的充流单壁碳纳米管波动分析[J]. 振动与冲击,2017,36(8):1−8. YU Yang,YANG Yang. Wave propagation of fluid-filled single-walled carbon nanotubes based on the nonlocal-strain gradient theory[J]. Journal of Vibration and Shock,2017,36(8):1−8.
[19] 夏桂云,曾庆元. 深梁理论的研究现状与工程应用[J]. 力学与实践,2015,37(3):302−316. DOI: 10.6052/1000-0879-14-080 XIA Guiyun,ZENG Qingyuan. Timoshenko beam theory and its applications[J]. Mechanics in Engineering,2015,37(3):302−316. DOI: 10.6052/1000-0879-14-080
[20] TIMOSHENKO S P. LXVI. On the correction for shear of the differential equation for transverse vibrations of prismatic bars[J]. The Philosophical Magazine:A Journal of Theoretical Experimental and Applied Physics,1921,41(245):744−746.
[21] 王妍,姚多喜,鲁海峰. 高水压作用下煤层底板隔水关键层弹性力学解[J]. 煤田地质与勘探,2019,47(1):127−132. DOI: 10.3969/j.issn.1001-1986.2019.01.019 WANG Yan,YAO Duoxi,LU Haifeng. Elastic mechanics solution of water proof key layer in coal seam floor under high water pressure[J]. Coal Geology & Exploration,2019,47(1):127−132. DOI: 10.3969/j.issn.1001-1986.2019.01.019
[22] 李博,刘子捷. 煤层底板富水承压溶洞突水力学模型构建及突水判据研究[J]. 煤炭科学技术,2022,50(5):232−237. LI Bo,LIU Zijie. Construction of mechanical model of water inrush from water-rich confined karst cave in coal seam floor and study on criterion[J]. Coal Science and Technology,2022,50(5):232−237.
[23] 刘泽威,刘其声,刘洋. 煤层底板隐伏断层分类及突水防治措施[J]. 煤田地质与勘探,2020,48(2):141−146. DOI: 10.3969/j.issn.1001-1986.2020.02.022 LIU Zewei,LIU Qisheng,LIU Yang. Classification of hidden faults in coal seam floor and measures for water inrush prevention[J]. Coal Geology & Exploration,2020,48(2):141−146. DOI: 10.3969/j.issn.1001-1986.2020.02.022
[24] HUANG Pinghua,HU Yongsheng,GAO Hongfei,et al. Dynamic identification and radium–radon response mechanism of floor mixed water source in high ground temperature coal mine[J]. Journal of Hydrology,2021,603(part B):126942.
[25] SUN Ming,GUO Chen,ZHENG Wenxiang,et al. Study on broken floor rock mass by mining underground pressure[J]. Mathematical Problems in Engineering,2021,2021:3797188.
[26] LI Qiang,MENG Xiangxi,LIU Yuben. Sensitivity analysis of water inrush evaluation model based on the theory of water resistant key strata:A case study in a coal mine,China[J]. Earth Science Informatics,2022,15(4):2481−2494. DOI: 10.1007/s12145-022-00851-2
[27] 段建华. 煤层底板突水综合监测技术及其应用[J]. 煤田地质与勘探,2020,48(4):19−28. DOI: 10.3969/j.issn.1001-1986.2020.04.003 DUAN Jianhua. Integrated monitoring technology of water inrush from coal seam floor and its application[J]. Coal Geology & Exploration,2020,48(4):19−28. DOI: 10.3969/j.issn.1001-1986.2020.04.003
[28] 虎维岳,赵春虎,吕汉江. 煤层底板水害区域注浆治理影响因素分析与高效布孔方式[J]. 煤田地质与勘探,2022,50(11):134−143. DOI: 10.12363/issn.1001-1986.22.04.0279 HU Weiyue,ZHAO Chunhu,LYU Hanjiang. Main influencing factors for regional pre-grouting technology of water hazard treatment in coal seam floor and efficient hole arrangement[J]. Coal Geology & Exploration,2022,50(11):134−143. DOI: 10.12363/issn.1001-1986.22.04.0279
[29] 马凯,尹立明,陈军涛,等. 深部开采底板隔水关键层受局部高承压水作用破坏理论分析[J]. 岩土力学,2018,39(9):3213−3222. MA Kai,YIN Liming,CHEN Juntao,et al. Theoretical analysis on failure of water-resisting key strata in the floor by local high confined water in deep mining[J]. Rock and Soil Mechanics,2018,39(9):3213−3222.
[30] 马凯. 受局部高承压水与多含水层影响的深部底板突水危险性理论分析与验证[D]. 青岛:山东科技大学,2019. MA Kai. Theoretical analysis and verification of water inrush danger in deep mining affected by local high confined water and multiple aquifers[D]. Qingdao:Shandong University of Science and Technology,2019.
[31] 姚明豪. 新桥煤矿底板隔水层结构特征与阻隔水能力研究[D]. 徐州:中国矿业大学,2019. YAO Minghao. Study on structural characteristics of the floor aquifuge and water-resisting ability of Xinqiao coalmine[D]. Xuzhou:China University of Mining and Technology,2019.
[32] 张建民,李全生,张勇,等. 煤炭深部开采界定及采动响应分析[J]. 煤炭学报,2019,44(5):1314−1325. ZHANG Jianmin,LI Quansheng,ZHANG Yong,et al. Definition of deep coal mining and response analysis[J]. Journal of China Coal Society,2019,44(5):1314−1325.
[33] 朱庆伟,李航,杨小虎,等. 采动覆岩结构演化特征及对地表沉陷的影响分析[J]. 煤炭学报,2019,44(增刊1):9−17. ZHU Qingwei,LI Hang,YANG Xiaohu,et al. Influence analysis of between subsidence and structure evolution in overburden rock under mining[J]. Journal of China Coal Society,2019,44(Sup.1):9−17.
[34] 吴家龙. 弹性力学[M]. 3版. 北京:高等教育出版社,2016. [35] 刘亮,胡玉茹,张元海. 用材料力学公式计算任意截面短梁正应力时的修正项研究[J]. 计算力学学报,2015,32(3):383−387. DOI: 10.7511/jslx201503014 LIU Liang,HU Yuru,ZHANG Yuanhai. Study on modification term for normal stress of short beam with arbitrary cross section by applying formula in material mechanics[J]. Chinese Journal of Computational Mechanics,2015,32(3):383−387. DOI: 10.7511/jslx201503014
[36] 徐芝纶. 弹性力学-下册[M]. 5版. 北京:高等教育出版社,2016. [37] 高荣誉,范家让. 叠层深梁的精确解[J]. 合肥工业大学学报(自然科学版),2009,32(5):738−741. GAO Rongyu,FAN Jiarang. An exact solution of deep laminated beams[J]. Journal of Hefei University of Technology (Natural Science),2009,32(5):738−741.
[38] 丁大钧,刘伟庆. 深梁杆件力学解[J]. 工程力学,1993,10(1):10−18. DING Dajun,LIU Weiqing. Solution of deep beams based on mechanics of bar system[J]. Engineering Mechanics,1993,10(1):10−18.
[39] 陈林之,李章政. 均布荷载作用下连续深梁问题的级数解答[J]. 机械,2005,32(9):30−32. CHEN Linzhi,LI Zhangzheng. Series solution for continuous deep beam subjected to uniform loads[J]. Machinery,2005,32(9):30−32.
[40] 刘鸿文. 材料力学(第五版)[M]. 北京:高等教育出版社,2014. [41] QIAN Minggao,MIAO Xiexing,Ll Liangjie. Mechanical behaviour of main floor for water inrush in longwall mining[J]. Journal of China University of Mining and Technology,1995(1):9−16.
计量
- 文章访问数: 113
- HTML全文浏览量: 2
- PDF下载量: 27
