Failure depths of stope floors under dynamic loading induced by roof breaking
-
摘要:目的
准确评估采场底板破坏深度对于底板突水危险性评价至关重要。传统理论模型计算时往往仅考虑采场支承压力和承压水压的静载作用,导致计算结果与实际情况存在较大偏差。因此,综合考虑深部底板破坏的多力源耦合作用,构建更加贴近实际的计算模型可为深部煤层底板水害的有效防治提供科学依据。
方法在明确顶板来压期间采场底板承受载荷的基础上,基于弹性动力学理论构建了动静载联合作用下的采场底板力学响应计算模型,得到了动载应力在底板中的传递规律以及底板动力响应特征,分析了顶板断裂动载扰动作用对采场底板破坏深度的影响规律;并以山东肥城某矿8031工作面为例,采用数值模拟和现场钻孔注水试验开展了工作面底板深度研究。
结果和结论结果表明:顶板断裂产生的动载与采场支承压力在底板产生的静载应力叠加,会对底板应力集中区和卸载区造成强烈扰动影响。在动载作用过程中,底板应力场集中程度和区域范围都明显增加;顶板断裂动载扰动会进一步加剧采场底板岩层的破坏,理论计算、模拟分析与现场实测得到初次来压动载扰动造成的采场底板二次破坏深度分别为5.9、6.6、6.3 m,三者结果相近,验证了理论模型的准确性。研究结果能够反映出底板突水发生时间和位置的规律,可为深部底板突水防治提供重要的理论依据和参考价值。
Abstract:ObjectiveAccurately assessing the failure depths of stope floors is crucial for assessing floor water inrush risks. Conventional theoretical models for calculating the failure depths generally merely consider static loads from the support pressure and confined water's pressure in stopes, leading to large deviations between calculation results and actual situations. Therefore, constructing a more practical computational model that comprehensively considers the coupled effects of multiple force sources on the failure of deep floors can provide a scientific basis for the effective prevention and control of water hazards in deep coal seam floors.
MethodsBased on the dynamic elasticity theory and the loads on a stope floor during roof weighting, this study constructed a computational model for the mechanical responses of the stope floor under combined static and dynamic loads. Using this model, this study determined the law of the transfer of dynamic load stress in the floor, as well as the dynamic response characteristics of the floor. Accordingly, this study analyzed the impacts of dynamic load disturbance induced by roof breaking on the failure depth of the stope floor. The constructed model was employed to investigate the floor failure depth of mining face 8031 within a coal mine in Feicheng, Shandong Province using numerical simulations and in-situ water injection tests in boreholes.
Results and ConclusionsThe results indicate that the dynamic loads induced by roof breaking were superimposed with the static load stress in the floor produced by the support pressure of the stope, leading to intense disturbances to the stress concentration and unloading zones of the floor. The degree and range of the stress field concentration on the floor increased significantly during dynamic loading. The dynamic load disturbance induced by roof breaking further intensified the failure of strata in the stope floor. The theoretical calculation, simulation analysis, and field measurement results revealed similar depths of 5.9, 6.6, and 6.3 m for the secondary floor failure caused by initial weighting-induced dynamic load disturbance, verifying the accuracy of the theoretical model. The results can reflect the laws of the time and locations of water inrushes on the floor, providing a significant theoretical basis and reference for the prevention and control of water inrushes from deep floors.
-
随着浅部煤炭资源的日益枯竭和煤矿开采强度的不断加大,我国各矿区都将相继进入深部开采状态[1-2]。深部开采面临的高水压环境导致底板水害威胁愈发严重,稍有疏忽就会出现重大灾害事故,底板突水隐患已成为我国深部煤炭资源开采的重要威胁之一[3-5]。
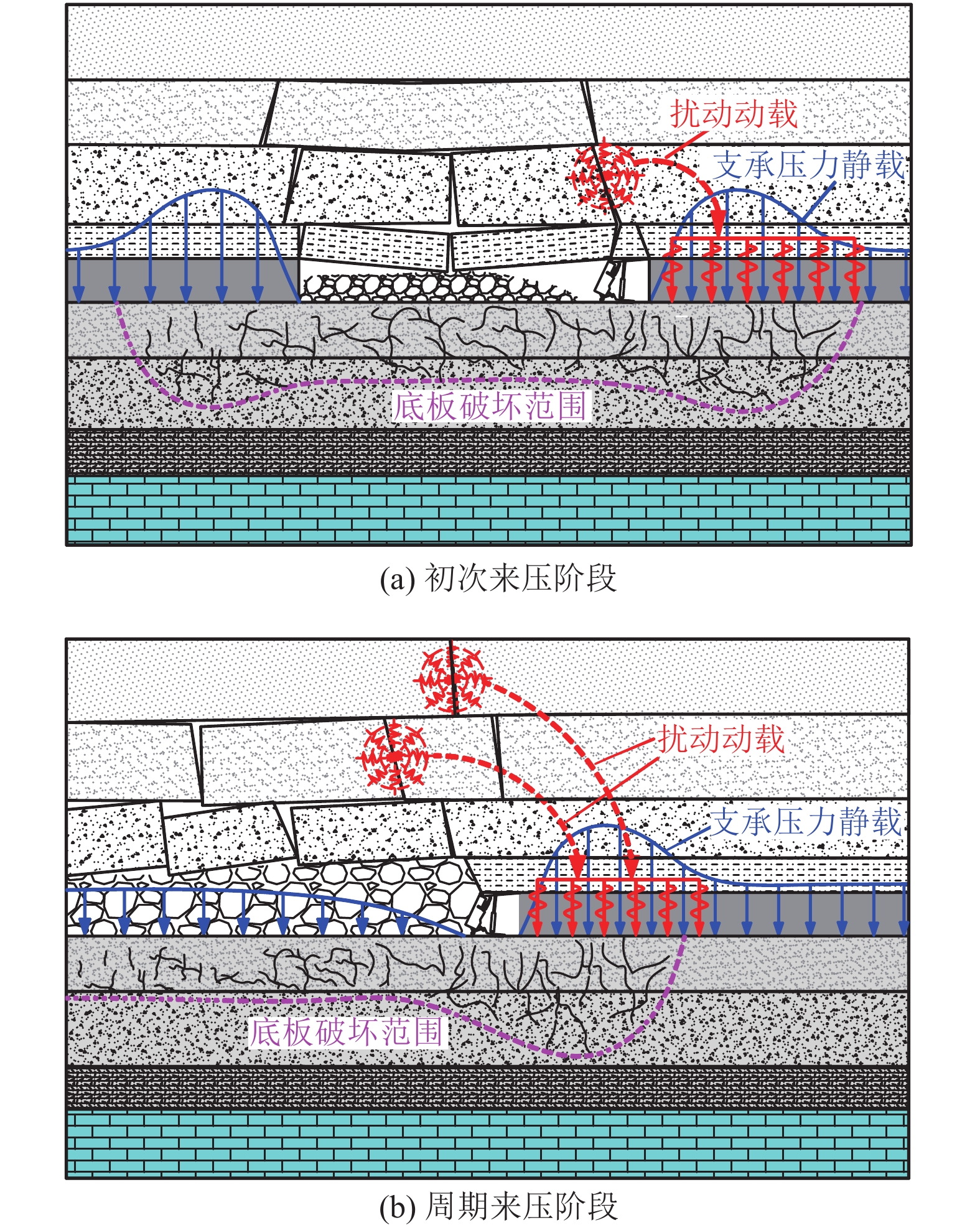
大量矿井突水事故实例表明,大多数的底板突水发生于工作面初次来压和周期来压期间[6-7]。从力学的角度分析,一方面是因为初次来压和周期来压期间,支承压力作用最强,底板破坏深度较大;另一方面是由于初次来压和周期来压时,底板会承受较大的动载荷作用,进一步加剧底板隔水层的破坏和导水裂隙的发育[8]。可见,动载对突水灾害的发生和发展影响较大,特别是对于深部采场底板,原岩应力高,底板岩层的应力集中更加明显,对动载扰动响应更加敏感。动载扰动对深部采场底板破坏突水作用也更加突出,近年来由于顶板断裂动载扰动诱发的底板突水事故屡见不鲜[9-12]。因此,如何研究总结深部采场底板突水灾害的演化规律和形成机理,特别是动载扰动作用对采场底板应力场分布及破坏规律的影响机制,仍是亟待解决的科学难题。
近年来,学者们在动载扰动诱发底板突水方面进行了大量研究探索。在底板突水规律方面,通过对煤开采过程中的采动应力与底板含水层水压、涌水量响应时空关系分析,发现含水层水压、底板出水点涌水量与工作面强烈来压之间表现为含水层滞后突水、降压现象,得到深部底板突水的主要特征是顶板垮落产生的强烈来压动载诱发所致[13-14]。动载扰动导致底板破坏方面,学者应用弹性理论推导出了动载扰动强度与底板破裂深度的关系模型[15];现场实测主要通过地质雷达、注水试验和应变探测等,对工作面底板采动破坏深度开展连续性监测[16-17],发现工作面周期来压产生的动力扰动对底板岩层的二次滞后破坏现象。此外,为了揭示底板破坏突水通道形成过程中的动力扰动效应,学者们还应用理论分析和数值模拟等手段研究了动载作用对深部岩体破坏特征[18]和断层活化规律[19]的影响。
综合分析,国内外学者已考虑到动载在突水灾害发生与演化过程中的诱导和触发作用,并在岩体动载破坏特征[20-22]、突水规律[23-24]和突水预警[25]等方面做了大量有益的探索。然而,由于深部工作面底板受动载作用时,会表现出很强的动态特征,这与静载作用下表现出的力学特性与破坏模式有很大的不同,动载扰动对深部采场底板突水的影响非常复杂[26]。鉴于此,笔者考虑工作面顶板初次来压和周期来压动载扰动对采场底板应力场与破坏深度的影响,建立动静载联合作用下的采场底板应力计算模型,研究动载应力在底板中的传递规律以及底板动力响应特征,并结合数值模拟及现场实测数据分析顶板来压动载扰动对底板破坏规律的影响机制,从而揭示底板突水灾害发生时间和位置的规律,以期为深部底板水害精准防控提供依据。
1 工程概况
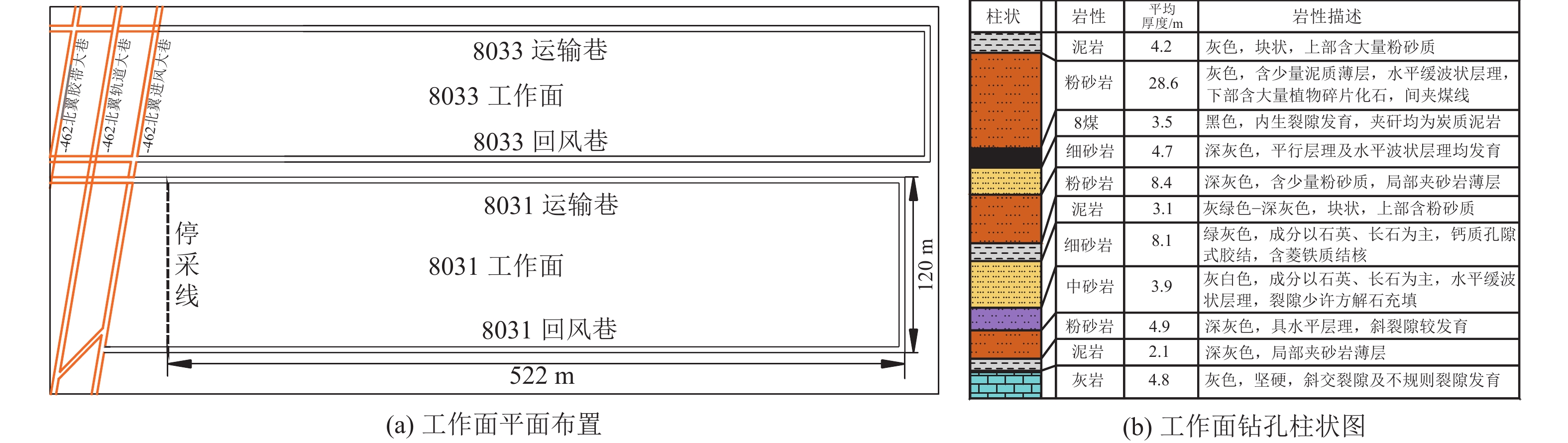
山东肥城某矿8031工作面开采煤层8煤,煤厚2.7~4.3 m,平均厚3.5 m;该煤层属于稳定−较稳定的近水平煤层,平均倾角为3°;工作面走向约522 m,斜长约120 m;工作面高程为−465~−495 m,平均采深约520 m。8031工作面为该采区的首采工作面,北侧为8033接续工作面,区段煤柱宽度为6 m(图1a)。工作面煤层直接顶为坚硬的厚层粉砂岩,厚度19.5~36.8 m,平均28.6 m,质较纯,厚层块状结构,局部裂隙较发育,属非常稳定顶板,大面积悬露不易垮落,初次来压步距L=36 m,周期垮落步距20~30 m。对工作面回采产生直接影响的底板含水层为石炭系本溪组徐家庄灰岩承压含水层,距离煤层底板约35.2 m。该含水层厚度一般为3.2~5.5 m,平均4.8 m(图1b),灰岩岩溶裂隙较发育,连通性较好,水压3.0 MPa左右,弱富水性。
8031工作面所在采区的各工作面均不同程度受到底板突水威胁,采区内多个工作面在回采初期底板无突水,但多次在顶板初次来压和周期来压期间发生底板突水事故。由此可见,工作面底板突水与顶板来压之间极具相关性,根据前人研究成果可推断其主要原因是由于开采深度大,底板岩层应力高度集中,加上顶板管理采用全部垮落法,上覆厚层坚硬顶板突然断裂时产生较强动载扰动作用,造成频繁剧烈来压影响,矿井底板出水呈动态变化。
2 采场底板动静载应力响应计算模型
2.1 动静载力学模型
根据矿山压力理论,煤层开采后,由于覆岩运动的影响,采场底板支承压力会发生变化,顶板来压期间采场底板承受的载荷如图2所示。工作面顶板初次来压和周期来压时,会伴随明显的动载扰动。因此,采场底板所承受的载荷主要包括:底板承压含水层产生的水压;采煤工作面采动后,采场上部未垮落岩层以“顶压”形式通过采场围岩向煤层底板传递支承压力静载;以及顶板周期来压期间由于顶板岩层断裂产生动载扰动作用,动载应力可表示为[27]:
$$ q\left( t \right) = \left\{\begin{aligned} & {\sigma _0}\sin \left( {2\pi \omega t} \right)\quad 0 \leqslant t \leqslant {t_1} \\ & 0\quad\qquad\qquad\;\;\; t \gt {t_1}\end{aligned} \right. $$ (1) 根据矿井微震监测[28],矿井动载强度一般为1.5~15.0 MPa,频率一般为几十到100 Hz,持续时间一般为0.01~0.10 s。
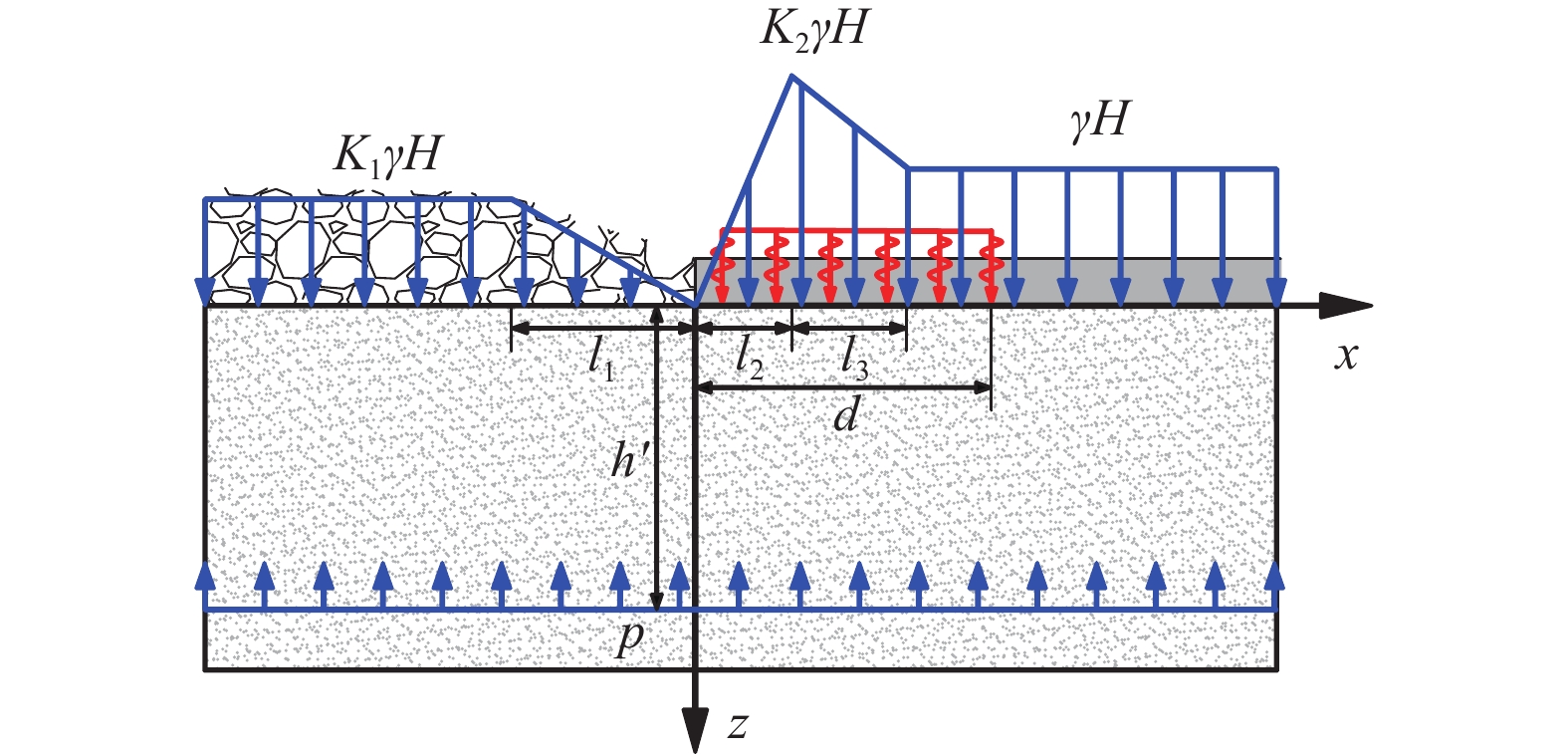
根据支承压力的分布特点,为了简化计算,对支承压力线性化处理,并以工作面位置为原点建立坐标系,工作面走向为x轴方向,z轴方向垂直向下,简化后的采场支承压力分布模型如图3所示。$ {K_1}\gamma H $为采空区内垮落带的载荷,对于初次来压,K1=0;$ {K_2}\gamma H $为工作面超前支承压力。此外,还考虑底板承压水压的影响。
基于上述底板受力模型,利用应力叠加原理求出动静载联合作用下底板任一点的垂直应力、水平应力和剪应力,从而分析顶板断裂动载对采场底板应力分布的影响规律。
2.2 理论计算方法
1)静载应力计算模型[29]
由支承压力$ q\left( x \right) $产生的静载应力场可根据半平面体受垂直分布力时任一点处的应力解求出,取微小长度dε,则底板静载应力场的求解公式为:
$$ \left\{ \begin{aligned} & {\sigma _{\textit{z}}} = \frac{2}{\pi }\int_{ - \infty }^{ + \infty } {\frac{{{{\textit{z}}^3}q\left( \varepsilon \right)}}{{{{\left[ {{{\left( {x - \varepsilon } \right)}^2} + {{\textit{z}}^2}} \right]}^2}}}} {\text{d}}\varepsilon \\ & {\sigma _x} = \frac{2}{\pi }\int_{ - \infty }^{ + \infty } {\frac{{{\textit{z}}{{\left( {x - \varepsilon } \right)}^2}q\left( \varepsilon \right)}}{{{{\left[ {{{\left( {x - \varepsilon } \right)}^2} + {{\textit{z}}^2}} \right]}^2}}}} {\text{d}}\varepsilon \\ & {\tau _{x{\textit{z}}}} = \frac{2}{\pi }\int_{ - \infty }^{ + \infty } {\frac{{{{\textit{z}}^2}\left( {x - \varepsilon } \right)q\left( \varepsilon \right)}}{{{{\left[ {{{\left( {x - \varepsilon } \right)}^2} + {{\textit{z}}^2}} \right]}^2}}}} {\text{d}}\varepsilon \end{aligned} \right. $$ (2) 2)动载应力场计算模型
根据弹性动力学基本原理,不计体力时,弹性介质的运动方程和物理方程可分别表示为:
$$ \left\{ \begin{aligned} & \frac{{\partial {\sigma _{\textit{z}}}}}{{\partial {\textit{z}}}} + \frac{{\partial {\tau _{x{\textit{z}}}}}}{{\partial x}} = \rho \frac{{{\partial ^2}w}}{{\partial {t^2}}} \\ & \frac{{\partial {\sigma _x}}}{{\partial x}} + \frac{{\partial {\tau _{x{\textit{z}}}}}}{{\partial {\textit{z}}}} = \rho \frac{{{\partial ^2}u}}{{\partial {t^2}}} \end{aligned} \right. $$ (3) $$ \left\{ \begin{aligned} & {\sigma _x} = \left( {\lambda + 2G} \right)\frac{{\partial u}}{{\partial x}} + \lambda \frac{{\partial w}}{{\partial {\textit{z}}}} \\ & {\sigma _{\textit{z}}} = \left( {\lambda + 2G} \right)\frac{{\partial w}}{{\partial {\textit{z}}}} + \lambda \frac{{\partial u}}{{\partial x}} \\ & {\tau _{x{\textit{z}}}} = G\left( {\frac{{\partial u}}{{\partial {\textit{z}}}} + \frac{{\partial w}}{{\partial x}}} \right) \end{aligned} \right. $$ (4) 其中,$\lambda = {{\mu E} \mathord{\left/ {\vphantom {{\mu E} {\left[ {\left( {1 + \mu } \right)\left( {1 - 2\mu } \right)} \right]}}} \right. } {\left[ {\left( {1 + \mu } \right)\left( {1 - 2\mu } \right)} \right]}}$,$G = {E \mathord{\left/ {\vphantom {E {2\left( {1 + \mu } \right)}}} \right. } {2\left( {1 + \mu } \right)}}$。
结合式(3)和式(4)可得:
$$ \left\{ \begin{aligned} & \frac{{\partial {\sigma _{\textit{z}}}}}{{\partial {\textit{z}}}} = \rho \frac{{{\partial ^2}w}}{{\partial {t^2}}} - \frac{{\partial {\tau _{x{\textit{z}}}}}}{{\partial x}} \\ & \frac{{\partial {\tau _{x{\textit{z}}}}}}{{\partial {\textit{z}}}} = \rho \frac{{{\partial ^2}u}}{{\partial {t^2}}} - \frac{\lambda }{{\lambda + 2G}}\frac{{\partial {\sigma _{\textit{z}}}}}{{\partial x}} - \frac{{4G\left( {\lambda + G} \right)}}{{\left( {\lambda + 2G} \right)}}\frac{{{\partial ^2}u}}{{\partial {x^2}}} \\ & \frac{{\partial u}}{{\partial {\textit{z}}}} = \frac{{{\tau _{x{\textit{z}}}}}}{G} - \frac{{\partial w}}{{\partial x}} \\ & \frac{{\partial w}}{{\partial {\textit{z}}}} = \frac{{{\sigma _{\textit{z}}}}}{{\lambda + 2G}} - \frac{\lambda }{{\lambda + 2G}}\frac{{\partial u}}{{\partial x}} \end{aligned} \right. $$ (5) 对式(5)的时间t进行Laplace变换,Laplace变换及其逆变换的定义为:
$$ \left\{ \begin{aligned} & \tilde f\left( {x,{\textit{z}},s} \right) = \int_0^{ + \infty } {f\left( {x,{\textit{z}},t} \right){{\mathrm{exp}}({ - st})}{\mathrm{d}}t} \\ & f\left( {x,{\textit{z}},t} \right) = \frac{1}{{2\pi {\mathrm{i}}}}\int_{\beta - {\mathrm{i}}\infty }^{\beta + {\mathrm{i}}\infty } {\tilde f\left( {x,{\textit{z}},s} \right){{\mathrm{exp}}({st})}{\mathrm{d}}s} \end{aligned} \right. $$ (6) 同时,由动载应力传递到采场底板时,底板的初始状态为静止,即有:
$$ \left\{ \begin{aligned} & {\left. {w\left( {x,{\textit{z}},t} \right)} \right|_{t = 0}} = 0\quad {\left. {w'\left( {x,{\textit{z}},t} \right)} \right|_{t = 0}} = 0 \\ & {\left. {u\left( {x,{\textit{z}},t} \right)} \right|_{t = 0}} = 0\quad {\left. { u'\left( {x,{\textit{z}},t} \right)} \right|_{t = 0}} = 0 \end{aligned} \right. $$ (7) 因此,式(5)经Laplace变换,可变为:
$$ \left\{ \begin{aligned} & \frac{{\partial {{\tilde \sigma }_{\textit{z}}}\left( {x,{\textit{z}},s} \right)}}{{\partial {\textit{z}}}} = \rho {s^2}\tilde w\left( {x,{\textit{z}},s} \right) - \frac{{\partial {{\tilde \tau }_{x{\textit{z}}}}\left( {x,{\textit{z}},s} \right)}}{{\partial x}} \\ & \frac{{\partial {{\tilde \tau }_{x{\textit{z}}}}\left( {x,{\textit{z}},s} \right)}}{{\partial {\textit{z}}}} = \rho {s^2}\tilde u\left( {x,{\textit{z}},s} \right) - \frac{\mu }{{1 - \mu }}\frac{{\partial {{\tilde \sigma }_{\textit{z}}}\left( {x,{\textit{z}},s} \right)}}{{\partial x}} - \\ &\qquad \frac{E}{{1 - {\mu ^2}}}\frac{{{\partial ^2}\tilde u\left( {x,{\textit{z}},s} \right)}}{{\partial {x^2}}} \\ & \frac{{\partial \tilde u\left( {x,{\textit{z}},s} \right)}}{{\partial {\textit{z}}}} = \frac{{2\left( {1 + \mu } \right)}}{E}{{\tilde \tau }_{x{\textit{z}}}}\left( {x,{\textit{z}},s} \right) - \frac{{\partial \tilde w\left( {x,{\textit{z}},s} \right)}}{{\partial x}} \\ & \frac{{\partial w\left( {x,{\textit{z}},s} \right)}}{{\partial {\textit{z}}}} = \frac{{\left( {1 + \mu } \right)\left( {1 - 2\mu } \right)}}{{E\left( {1 - \mu } \right)}}{{\tilde \sigma }_{\textit{z}}}\left( {x,{\textit{z}},s} \right) - \frac{\mu }{{1 - \mu }}\frac{{\partial \tilde u\left( {x,{\textit{z}},s} \right)}}{{\partial x}} \end{aligned} \right. $$ (8) 为求解式(8),对x进行Fourier变换,Fourier变换及其逆变换的定义为:
$$ \left\{ \begin{aligned} & \left( {\bar u,{{\bar \sigma }_{\textit{z}}},{{\bar \tau }_{x{\textit{z}}}},\bar w} \right) = \int_{ - \infty }^\infty {\left( {u,{\sigma _{\textit{z}}},{\tau _{x{\textit{z}}}},w} \right){{\mathrm{exp}}({{\mathrm{i}}\xi x})}{\text{d}}x} \\ & \left( {u,{\sigma _{\textit{z}}},{\tau _{x{\textit{z}}}},w} \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {\left( {\bar u,{{\bar \sigma }_{\textit{z}}},{{\bar \tau }_{x{\textit{z}}}},\bar w} \right){{\mathrm{exp}}({ - {\mathrm{i}}\xi x})}{\text{d}}\xi } \end{aligned} \right. $$ (9) 则式(8)经Fourier变换,并写成矩阵形式为:
$$ \dfrac{\partial }{{\partial {\textit{z}}}}\left[ {\begin{array}{*{20}{c}} {{\mathrm{i}}{{\bar {\tilde \sigma} }_{\textit{z}}}\left( {\xi ,{\textit{z}},s} \right)} \\ {{{\bar {\tilde \tau} }_{x{\textit{z}}}}\left( {\xi ,{\textit{z}},s} \right)} \\ {\bar {\tilde u}\left( {\xi ,{\textit{z}},s} \right)} \\ {{\mathrm{i}}\bar {\tilde w}\left( {\xi ,{\textit{z}},s} \right)} \end{array}} \right] =\\ \left[ {\begin{array}{*{20}{c}} 0&\xi &0&{\rho {s^2}} \\ { - \dfrac{\mu }{{1 - \mu }}\xi }&0&{\rho {s^2} + \dfrac{E}{{1 - {\mu ^2}}}{\xi ^2}}&0 \\ 0&{\dfrac{{2\left( {1 + \mu } \right)}}{E}}&0&{ - \xi } \\ {\dfrac{{\left( {1 + \mu } \right)\left( {1 - 2\mu } \right)}}{{E\left( {1 - \mu } \right)}}}&0&{\dfrac{\mu }{{1 - \mu }}\xi }&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathrm{i}}{{\bar {\tilde \sigma} }_{\textit{z}}}\left( {\xi ,{\textit{z}},s} \right)} \\ {{{\bar {\tilde \tau} }_{x{\textit{z}}}}\left( {\xi ,{\textit{z}},s} \right)} \\ {\bar {\tilde u}\left( {\xi ,{\textit{z}},s} \right)} \\ {{\mathrm{i}}\bar {\tilde w}\left( {\xi ,{\textit{z}},s} \right)} \end{array}} \right] $$ (10) 令状态分量$ \bar {\tilde {\boldsymbol{\varPsi}}} = {\left[ {\begin{array}{*{20}{c}} {{\mathrm{i}}{{\bar {\tilde \sigma} }_{\textit{z}}}}&{{{\bar {\tilde \tau} }_{x{\textit{z}}}}}&{\bar {\tilde u}}&{{\mathrm{i}}\bar {\tilde w}} \end{array}} \right]^{\mathrm{T}}} $,则公式(10)可转变为如下的微分方程组:
$$ \frac{{\partial \bar {\tilde {\boldsymbol{\varPsi}}} \left( {\xi ,{\textit{z}},s} \right)}}{{\partial {\textit{z}}}} = {\boldsymbol{A}}\left( {\rho ,E,\mu ,\xi ,s} \right)\bar {\tilde {\boldsymbol{\varPsi}}} \left( {\xi ,{\textit{z}},s} \right) $$ (11) 据矩阵微积分计算,式(9)的解可表示为:
$$ \bar {\tilde {\boldsymbol{\varPsi}}} \left( {\xi ,{\textit{z}},s} \right) = \exp \left[ {{\textit{z}}{\boldsymbol{A}}\left( {\rho ,E,\mu ,s,\xi } \right)} \right]\bar {\tilde {\boldsymbol{\varPsi}}} \left( {\xi ,0,s} \right) $$ (12) 令$ {\boldsymbol{G}}\left( {\rho ,E,\mu ,\xi ,{\textit{z}},s} \right) = \exp \left[ {{\textit{z}}{\boldsymbol{A}}\left( {\rho ,E,\mu ,\xi ,s} \right)} \right] $,式(12)矩阵形式为:
$$ \left[ {\begin{array}{*{20}{c}} {\text{i}{{\bar {\tilde \sigma} }_{\textit{z}}}\left( {\xi ,{\textit{z}},s} \right)} \\ {{{\bar {\tilde \tau} }_{x{\textit{z}}}}\left( {\xi ,{\textit{z}},s} \right)} \\ {\bar {\tilde u}\left( {\xi ,{\textit{z}},s} \right)} \\ {\text{i}\bar {\tilde w}\left( {\xi ,{\textit{z}},s} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{G_{11}}}&{{G_{12}}}&{{G_{13}}}&{{G_{14}}} \\ {{G_{21}}}&{{G_{22}}}&{{G_{23}}}&{{G_{24}}} \\ {{G_{31}}}&{{G_{32}}}&{{G_{33}}}&{{G_{34}}} \\ {{G_{41}}}&{{G_{42}}}&{{G_{43}}}&{{G_{44}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\text{i}{{\bar {\tilde \sigma} }_{\textit{z}}}\left( {\xi ,0,s} \right)} \\ {{{\bar {\tilde \tau} }_{x{\textit{z}}}}\left( {\xi ,0,s} \right)} \\ {\bar {\tilde u}\left( {\xi ,0,s} \right)} \\ {\text{i}\bar {\tilde w}\left( {\xi ,0,s} \right)} \end{array}} \right] $$ (13) 其中:
$$ {G_{11}} = {G_{44}} = \left( {1 + B\xi } \right){{\mathrm{cosh}}} \left( {M{\textit{z}}} \right) - B\xi {{\mathrm{cosh}}} \left( {N{\textit{z}}} \right) \text{,} $$ $$ {G_{12}} = BN{{\mathrm{sinh}}} \left( {N{\textit{z}}} \right) - \frac{{\xi \left( {1 + B\xi } \right)}}{M}{{\mathrm{sinh}}} \left( {M{\textit{z}}} \right) \text{,} $$ $$ {G_{13}} = - {G_{24}} = \rho {s^2}B\left( {1 + B\xi } \right)\left[ {{{\mathrm{cosh}}} \left( {N{\textit{z}}} \right) - {{\mathrm{cosh}}} \left( {M{\textit{z}}} \right)} \right] \text{,} $$ $$ {G_{14}} = \frac{{\rho {s^2}{{\left( {1 + B\xi } \right)}^2}}}{M}{{\mathrm{sinh}}} \left( {M{\textit{z}}} \right) - \rho {s^2}{B^2}N{{\mathrm{sinh}}} \left( {N{\textit{z}}} \right) \text{,} $$ $$ {G_{21}} = - {G_{43}} = BM{{\mathrm{sinh}}} \left( {M{\textit{z}}} \right) - \frac{{\xi \left( {1 + B\xi } \right)}}{N}{{\mathrm{sinh}}} \left( {N{\textit{z}}} \right) \text{,} $$ $$ {G_{22}} = {G_{33}} = \left( {1 + B\xi } \right){{\mathrm{cosh}}} \left( {N{\textit{z}}} \right) - B\xi {{\mathrm{cosh}}} \left( {M{\textit{z}}} \right) \text{,} $$ $$ {G_{23}} = \frac{{\rho {s^2}{{\left( {1 + B\xi } \right)}^2}}}{N}{{\mathrm{sinh}}} \left( {N{\textit{z}}} \right) - \rho {s^2}{B^2}M{{\mathrm{sinh}}} \left( {M{\textit{z}}} \right) \text{,} $$ $$ {G_{31}} = - {G_{42}} = \frac{{\xi \left[ {{{\mathrm{cosh}}} \left( {M{\textit{z}}} \right) - {{\mathrm{cosh}}} \left( {N{\textit{z}}} \right)} \right]}}{{\rho {s^2}}} \text{,} $$ $$ {G_{32}} = \frac{1}{{\rho {s^2}}}\left[ {N{{\mathrm{sinh}}} \left( {N{\textit{z}}} \right) - \frac{{{\xi ^2}}}{M}{{\mathrm{sinh}}} \left( {M{\textit{z}}} \right)} \right] \text{,} $$ $$ {G_{34}} = \frac{{\left( {1 + B\xi } \right)\xi }}{M}{{\mathrm{sinh}}} \left( {M{\textit{z}}} \right) - BN{{\mathrm{sinh}}} \left( {N{\textit{z}}} \right) \text{,} $$ $$ {G_{41}} = \frac{1}{{\rho {s^2}}}\left[ {M{{\mathrm{sinh}}} \left( {M{\textit{z}}} \right) - \frac{{{\xi ^2}}}{N}{{\mathrm{sinh}}} \left( {N{\textit{{\textit{z}}}}} \right)} \right] \text{,} $$ $$ B = \frac{{E\xi }}{{\rho {s^2}\left( {1 + \mu } \right)}} \text{,} M = \sqrt {\frac{{\rho {s^2}\left( {1 - 2\mu } \right)\left( {\mu + 1} \right)}}{{E\left( {1 - \mu } \right)}} + {\xi ^2}} \text{,} $$ $$ N = \sqrt {\frac{{2\rho {s^2}\left( {\mu + 1} \right)}}{E} + {\xi ^2}} 。 $$ 对于采场底板任意深度h与表面状态向量的关系为:
$$ \bar {\tilde {\boldsymbol{\varPsi}}} \left( {\xi ,{\textit{z}},s} \right) = {\boldsymbol{G}}\left( {\rho ,E,\mu ,\xi ,h,s} \right) \cdot \bar {\tilde {\boldsymbol{\varPsi}}} \left( {\xi ,0,s} \right) $$ (14) 在底板顶部($ {\textit{z}} = 0 $)和无穷深处($ {\textit{z}} = \infty $)的边界条件可表示为:
$$ \left\{\begin{aligned} & {\left. {{\sigma _{\textit{z}}}\left( {x,{\textit{z}},t} \right)} \right|_{{\textit{z}} = 0}} = q\left( t \right) \\ & {\left. {{\tau _{x{\textit{z}}}}\left( {x,{\textit{z}},t} \right)} \right|_{{\textit{z}} = 0}} = 0 \\ & {\left. {u\left( {x,{\textit{z}},t} \right)} \right|_{{\textit{z}} = \infty }} = {\left. {w\left( {x,{\textit{z}},t} \right)} \right|_{{\textit{z}} = \infty }} = 0 \end{aligned} \right. $$ (15) 将式(15)进行对t的Laplace变换和x的Fourier变换后,代入式(14),即可求得工作面底板动力学响应解。
利用Matlab编程分别求解采场底板受静载和动载作用时的垂直应力、水平应力和剪应力,并利用矢量叠加,得到采场底板各位置的3个应力分量随动力加载时间的变化,从而分析顶板断裂产生的动载在底板岩层中的传播规律,及其对采场底板应力场分布的影响,并在此基础上揭示动静载联合作用下采场底板应力响应特征。
2.3 底板动应力响应特征
根据工作面实际开采资料和现场观测结果:底板岩层参数取平均值,弹性模量E=16.6 GPa,泊松比μ=0.25,密度ρ=2 650 kg/m3。初次来压时超前支承压力应力增高区长度l2= 10 m、l3= 25 m,γH=10 MPa,应力集中系数K2=2.1,底板含水层承压水压p=3 MPa。
根据工作面回采时的微震监测结果,初次来压时深入煤壁的上边缘处顶板断裂释放大量弹性能,顶板关键层断裂产生的附加动载应力可表示为[30]:
$$ {\sigma _0} = \rho '\zeta {v_{\mathrm{f}}} $$ (16) $$ {v_{\mathrm{f}}} = {\left( {{{2K\eta U{l^{ - \lambda }}} / {\rho '}}} \right)^{{1 / 2}}} $$ (17) 其中顶板初次破坏前聚集的弹性能U[31]可表示为:
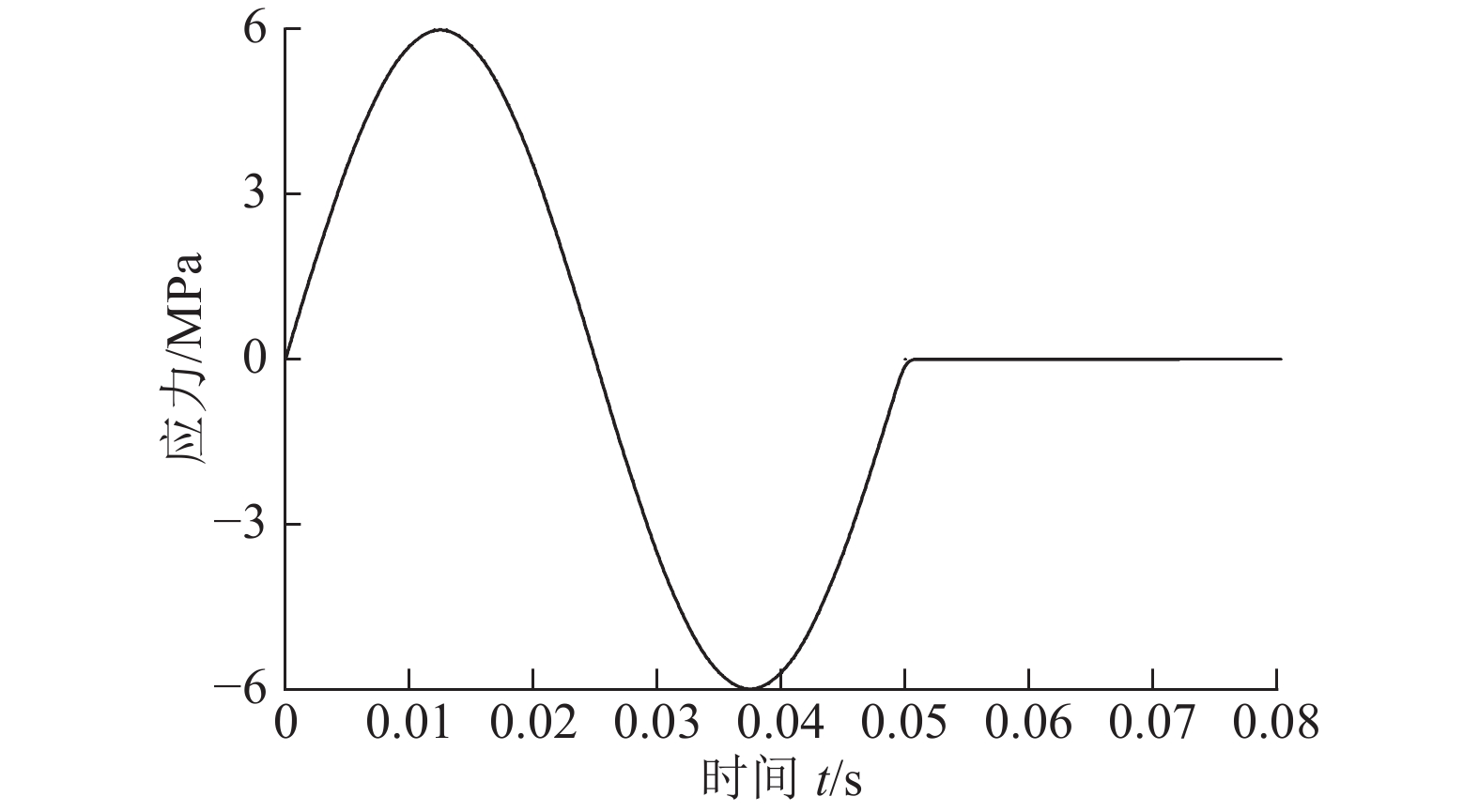
$$ U = {{{q^2}{L^5}{d_1}} \mathord{\left/ {\vphantom {{{q^2}{L^5}{d_1}} {\left( {48{E_1}{h_1}^3} \right)}}} \right. } {\left( {48{E_1}{h_1}^3} \right)}}$$ (18) 结合工作面实际开采参数,并取矿震能量作用系数K=0.03,岩层介质密度$ \rho ' $=2 600 kg/m3,动载传播速度ζ=3 000 m/s,震源到底板最近距离s=25 m,衰减系数λ=1.5,地震效应η=0.9%,将以上参数代入式(16)和式(17)中,可得到顶板对底板施加的动应力$ {\sigma _0} $=6.0 MPa。另根据微震监测数据$ \omega $=20 Hz,t1=0.05 s,同时考虑动力计算效率,动载作用计算时间设为0.1 s,作用范围d=20 m,简化动载应力时程曲线如图4所示。
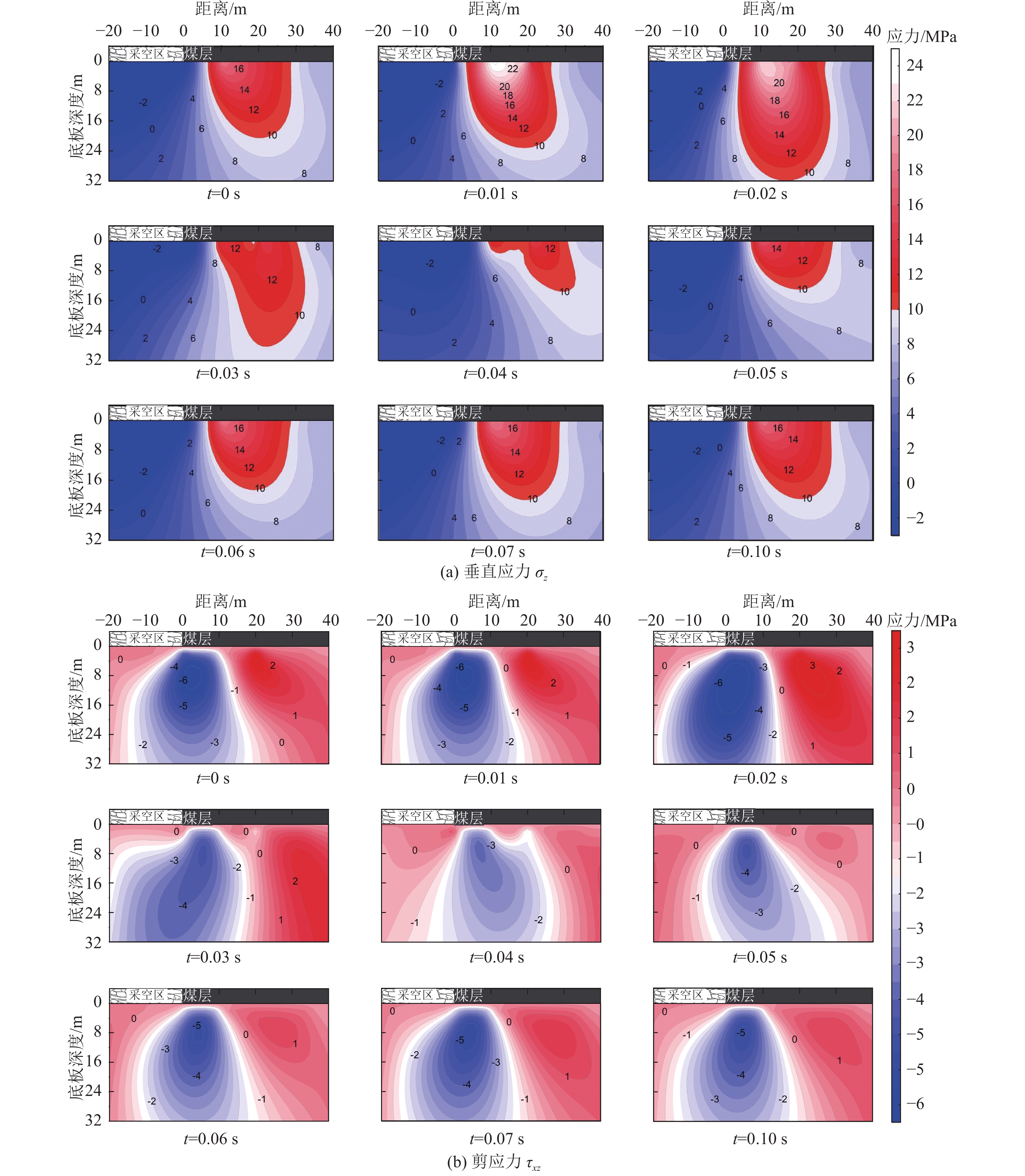
将以上参数代入理论计算模型,即可得到动载作用过程中的采场底板垂直应力和剪应力的响应过程(图5)。
由图5a可知,动载作用前(t=0 s),工作面底板仅受到采场支承压力和承压水压静载的作用。由于支承压力作用,底板垂直应力场呈非均匀分布,采空区下底板处于卸压区,未采区下底板处于应力集中区,最大垂直应力σz达到17.7 MPa,位于离工作面约10 m处的未采区底板,垂直应力集中区的影响深度约为20 m。t=0.01~0.05 s时,动载应力向底板深处传递,与支承压力产生的静载应力叠加,对采场底板应力场分布产生较大影响,底板应力场非均匀性进一步加剧,动载作用范围内的底板整体应力水平明显提高,未采区底板所形成的应力集中程度和应力集中区范围不断扩大,其中垂直应力σz峰值达到24.4 MPa,较静载作用时增加约37.9%;垂直应力最大影响深度达32 m,增加约60%。t=0.06 s时,动载应力作用已完成,但动载产生的应力持续影响底板,使得底板应力场一直处于动态变化状态,底板的应力集中和卸压程度也处于动态变化状态;t=0.10 s时,由于衰减作用,采场底板的动力响应基本完成,此时的底板应力场与动载作用前基本一致。
同理,从图5b可以得到,在支承压力和承压水压静载作用下(t=0 s),在未采区底板内形成剪应力集中区,最大剪应力达6.4 MPa,正负剪应力呈反对称分布形式,由此可推断剪应力较大位置的底板容易发生剪切破坏,形成底板导水通道;动载应力传递到底板,对底板剪应力分布产生较大影响,最大剪应力增加到7.0 MPa,较静载作用时增加约12.5%,水平和深度影响范围都进一步扩大。
2.4 底板破坏深度分析
根据前述分析可知,动载作用会造成底板岩层的应力分布发生调整,必然会对采场底板破坏的范围产生直接的影响。底板最大破坏深度一般为剪切破坏,故根据Mohr-Coulomb屈服破坏准则,采场底板岩层发生剪切破坏时的应力状态满足[32]:
$$ F\left( {x,{\textit{z}}} \right) = \left[ {\frac{{{\sigma _x} + {\sigma _{\textit{z}}}}}{2} + \frac{c}{{\tan \varphi }}} \right]\sin \varphi - \sqrt {{{\left( {\frac{{{\sigma _x} - {\sigma _{\textit{z}}}}}{2}} \right)}^2} + {\tau _{x{\textit{z}}}}^2} \gt 0 $$ (19) 其中:$ \varphi $和$ c $取底板岩层参数的平均值:$ \varphi $=34°,c = 2.4 MPa。并将相关参数代入,计算得到动载作用下底板累积破坏深度演化规律,如图6所示。
由图6可以得出:t=0 s时为支承压力静载造成的底板最大破坏深度为12.6 m;随着动载应力在底板中的传递,底板累积破坏深度逐渐增加,0.025 s之前,动载为压应力阶段,底板应力集中水平增加,底板累积破坏深度快速增加;0.025 s以后,动载应力转为拉应力,但由于动载应力的传递效应,累积破坏深度仍持续增大;0.05 s时动载作用完成,底板最大破坏深度达17.9 m;最终底板最大破坏深度达到18.5 m,较支承压力静载作用增加了5.9 m,增幅达46.8%。
3 数值模拟分析
3.1 模型构建与模拟方案
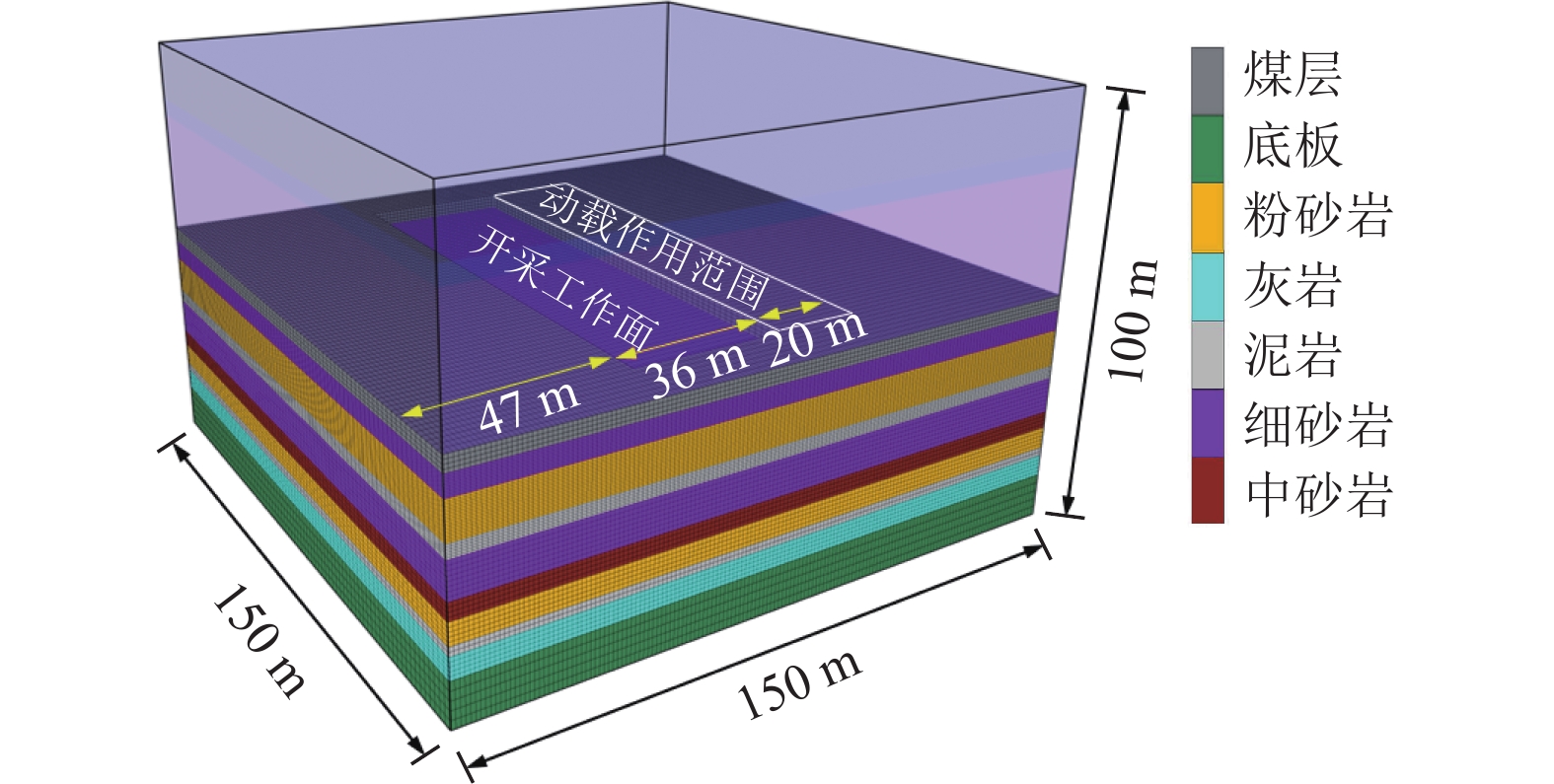
根据工作面的主要地质条件和开采参数,数值模型长150 m,宽150 m,高100 m,具体如图7所示。模型上部施加均布载荷9 MPa以代替500 m埋深时的上部岩体自重,底板灰岩含水层承压水压为3 MPa,计算采用Mohr-Coulomb本构模型。在室内岩石力学实验数据的基础上,按照一定的折减系数,得到与现场较为相符的数值模型力学参数见表1。
表 1 各岩层物理力学参数Table 1. Physical and mechanical parameters for various rock layers岩层名称 弹性模量/
GPa泊松比 内摩擦
角/(°)黏聚力/
MPa抗拉强度/
MPa密度/
(kg·m−3)上覆岩层 30.79 0.27 35 2.6 2.8 2 500 泥岩1 23.50 0.28 33 2.2 1.8 2 570 粉砂岩1 18.01 0.25 26 2.8 1.7 2 650 8煤 13.08 0.23 23 1.2 0.8 1 620 细砂岩1 29.18 0.26 34 3.1 2.4 2 630 粉砂岩2 21.80 0.25 32 4.8 3.2 2 350 泥岩2 10.62 0.31 28 2.2 1.0 2 400 细砂岩2 21.75 0.29 32 2.6 1.3 2 380 中砂岩 18.50 0.25 34 4.5 2.8 2 700 粉砂岩3 20.33 0.21 31 3.8 2.5 2 680 泥岩3 8.21 0.35 35 2.1 2.9 2 650 灰岩 35.74 0.23 37 4.5 2.6 2 450 底部岩层 44.21 0.20 39 5.6 2.8 2 760 模拟时先进行开挖后的静力分析,在静力平衡基础上进行工作面开挖,工作面斜长为120 m,工作面从x=47 m处开挖,推进长度为初次来压步距36 m。开挖静力平衡后,进行动力分析,利用内置的Fish语言编译动载应力时程函数,动载曲线如图4所示。将动载荷以均布的形式施加到邻近工作面20 m范围内的煤层顶板。本次模拟中最小临界阻尼比取0.02;最小中心频率通过对模型在重力作用下的无阻尼计算得到的自振频率来确定,计算结果为10 Hz。
3.2 模拟结果分析
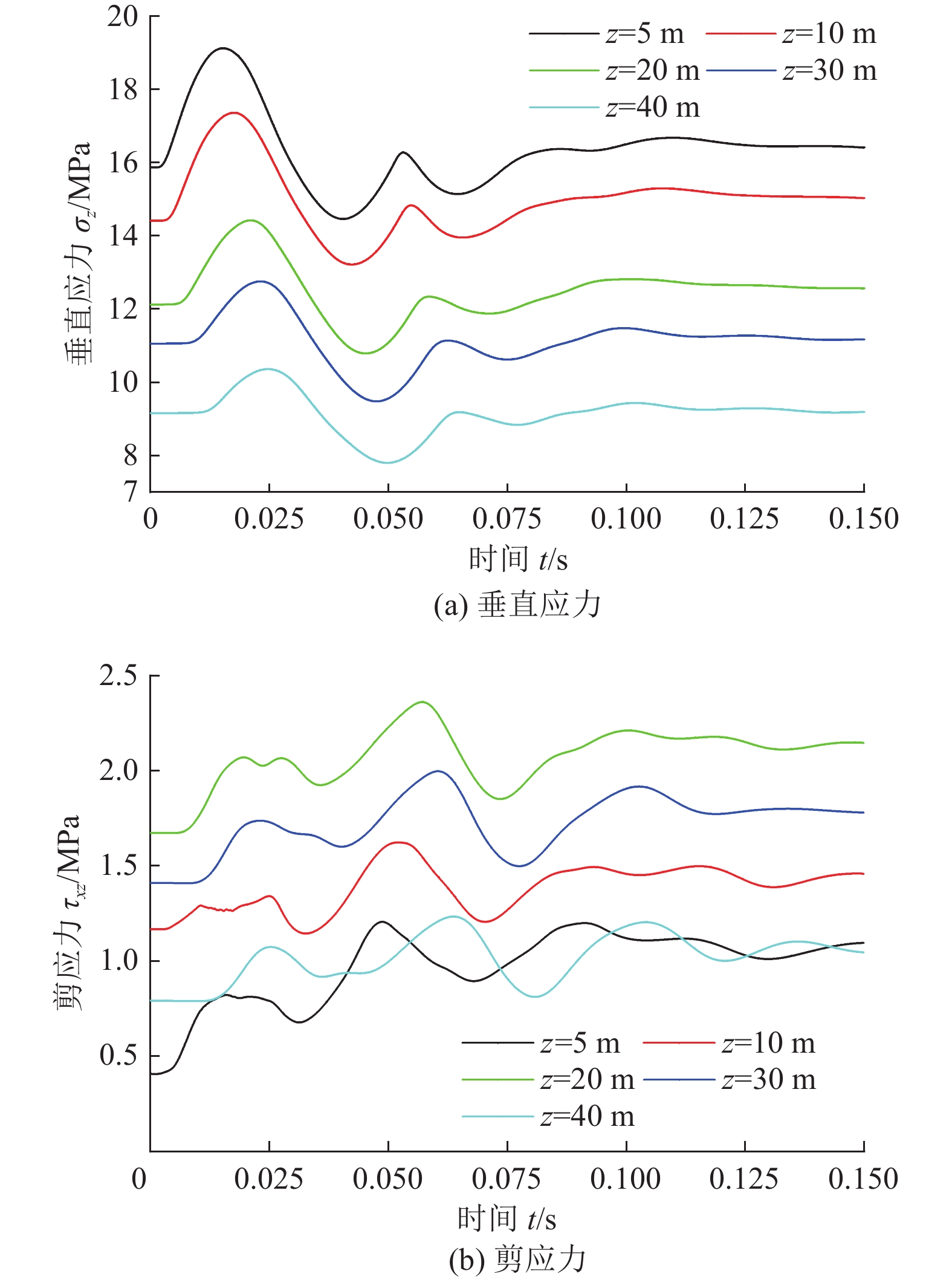
为得到动载扰动作用下底板应力响应规律,在动载作用中心位置的底板不同深度处布置应力监测点,各测点的垂直应力和剪应力变化曲线如图8所示。
由图8可知,动载作用引起底板不同深度处的垂直应力和剪应力都发生明显变化,随着时间变化应力呈现波动特征,各监测点的应力响应均与时间呈正弦函数关系,与动载应力呈相同的波动特征;且不同深度处底板应力响应存在差异性,随着底板深度的增加,应力响应时刻出现越晚,具有明显的动载传递特征。
图8a中各监测点的垂直应力增量随底板深度的增加而减小,距离底板5、10、20、30、40 m,动载引起底板最大垂直应力增量分别为3.25、2.95、2.31、1.70、1.21 MPa,表明动载应力呈现明显的衰减特征,底板动力响应随着深度的增加而降低。图8b中动载作用引起的底板不同深度处的最大剪应力都较动载作用前更大,表明动载作用会导致底板剪应力集中程度增大,造成底板剪切破坏深度进一步增加。此外,动载作用前,随着深度增加,底板剪应力先增大后减小,最大剪应力位于底板20 m处。动载作用后底板剪应力整体升高,距离底板20 m处的剪应力由动载作用前的1.67 MPa增加为2.36 MPa,增加约41.3%。综上分析,顶板断裂动载应力传递到底板,与静载应力场叠加,底板应力场出现明显波动,造成底板的应力状态呈现出动态集中现象,底板卸压区和应力集中区的动态变化会打破平衡状态,必然会加剧底板的破坏。
动载扰动作用下,底板破坏情况可通过塑性区分布变化直接反映,动载作用前后模型中部处的底板塑性区分布如图9所示。工作面初次来压前,在采场支承压力静载的作用下,底板破坏区形状类似于倒置马鞍状(图9a),在采空区下底板处于卸荷拉破坏区,底板最大破坏深度位于切眼和工作面处,达到11.6 m。顶板初次来压动载作用后底板区呈非均匀状(图9b),动载直接作用的工作面处底板最大破坏深度18.2 m,增加6.6 m,增加幅值约56.9%;切眼处底板也受到了动载作用的影响,最大破坏深度达13.6 m,增加了2.0 m。同时,对比数值模拟所得的动载作用前后底板最大破坏深度与理论计算结果非常相似,一定程度上证明了理论求解的正确性。
综上所述,顶板初次来压时产生的动载应力传递到煤壁附近的底板岩层内,与采场支承压力静载叠加,使原本处于极限状态下的底板岩层达到或超过强度极限发生失稳破坏,从而进一步加剧底板隔水层的破坏和导水裂隙的发育。因此,工作面初次来压和周期来压期间,容易在切眼和终采线附近底板产生突水点,当工作面在构造破坏带附近来压时,突水的可能性更大[33]。
4 底板破坏深度实测
4.1 探测方法与方案
钻孔注水试验是直观反映底板岩体裂隙发育特征的方法,也是目前已成熟、被广泛应用于煤矿底板破坏深度的探测方法[34-35]。根据工作面地质条件,采用“双端封堵测漏装置”对煤层底板不同深度的注水量进行探测分析。如图10所示,利用8033工作面回风巷作为观测巷道,在离切眼35 m处向工作面底板施工3个观测钻孔,钻孔水平间距3 m,钻孔钻至工作面垂深约30 m位置。在煤层开采前,以及工作面推进30、35和40 m时进行了4次井下注水试验,观测钻孔注水漏失量的变化,通过钻孔注水量变化分析底板破坏深度,相关钻孔参数见表2。
表 2 底板注水观测钻孔参数Table 2. Parameters for observation boreholes in the floor钻孔号 方位角/(°) 倾角/(°) 孔长/m 垂深/m 孔径/mm 1号 197 40 48 30 89 2号 197 51 38 30 89 3号 197 65 33 30 89 4.2 实测结果分析
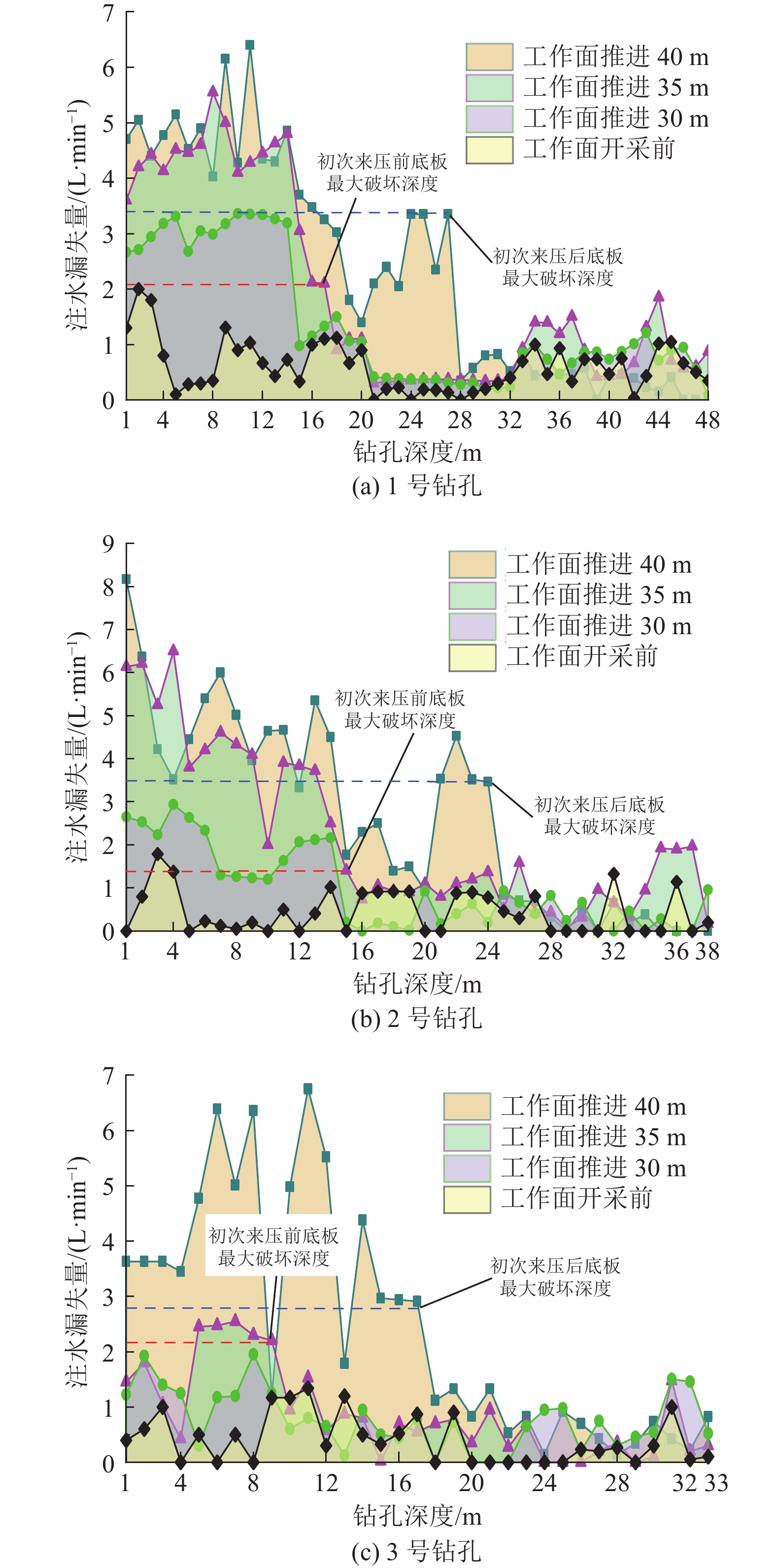
通过对各钻孔进行分段压水试验,记录钻孔不同深度流量稳定后的漏失量数据,绘制钻孔的漏失量曲线,从而得到不同观测阶段各钻孔的注水漏失量变化,如图11所示。
由图11a可知,工作面开采之前,底板岩体未受到开采扰动,1号钻孔注水漏失量范围在0~2 L/min。工作面推进30 m处,此时工作面距1号钻孔5 m,底板岩体受采动影响,钻孔14 m深度范围内的注水漏失量显著增加,达到2.6~3.5 L/min,平均3.1 L/min,明显高于采前注水漏失量,说明此区域各孔段围岩裂隙较发育,且在一定范围内裂隙相互贯通,计算可得此时的底板破坏深度为9 m。工作面推进35 m处,此时钻孔位于工作面正下方,钻孔18 m深度范围内注水漏失量变化明显,表明底板破坏深度增加至11.6 m。工作面推进至36 m处,工作面初次来压,继续推进至40 m处,测得资料显示1号钻孔27 m深度范围内的注水漏失量达到1.4~6.4 L/min,相对工作面采动前和初次来压前变化较大,计算可确定此时的底板最大破坏位置位于钻孔27 m深度处,即底板最大破坏深度达到17.4 m。
同理,根据图11b中2号钻孔不同时期的注水漏失量变化分析可得,工作面推进到35 m时,钻孔15 m深度范围内的围岩裂隙较发育,计算可得此时底板最大破坏深度为11.7 m。工作面推进至40 m时,经历顶板初次来压,2号钻孔24 m深度范围内注水漏失量变化明显,说明此时底板最大破坏深度达到18.7 m。由图11c可知,3号钻孔也表现出相似的规律,工作面推进35 m时,钻孔内9 m深度范围内漏失量变化明显,对应的底板最大破坏深度为8.2 m;工作面推进到40 m时,由于顶板初次来压动载的影响,底板最大破坏深度增加到15.4 m。
综合分析可知,工作面初次来压前,由于采动支承压力的影响,底板破坏深度为8.2~11.7 m;工作面初次来压后,3个钻孔不同深度均出现了注水漏矢量增加,即初次来压导致底板破坏深度加深现象,最大破坏深度增加了5.8~7.2 m,平均6.3 m。表明由于顶板初次来压的动载扰动作用,造成了底板二次破坏。同时可得到现场实测底板最大破坏深度为18.7 m,与理论分析和数值模拟计算结果基本一致,从而验证了理论模型的准确性。
5 结 论
(1)考虑到顶板初次来压和周期来压期间产生的动载对工作面底板应力场和破坏深度的影响,基于弹性动力学理论建立了动静载联合作用下的深部采场底板力学响应计算模型,并通过理论求解分析了顶板断裂动载与采场支承压力静载联合作用下的底板应力场响应规律。
(2)顶板岩体断裂产生的动载扰动使得采场底板应力场变化相对于单独的支承压力静载作用更为复杂,底板的各类应力都呈现出明显的动态特征。随着动载应力向底板深部传递,会对底板应力集中区和卸荷区造成强烈扰动影响,动载作用过程中的底板应力场集中程度和区域范围都明显增加。
(3)通过数值模拟和现场实测研究了初次来压动载扰动对底板破坏深度的影响,发现动载作用会进一步加剧采场底板岩层的破坏和导水裂隙的发育。理论计算、模拟分析与现场实测得到初次来压动载扰动造成的采场底板二次破坏深度分别为5.9、6.6和6.3 m,三者结果比较吻合,验证了理论模型的正确性和可行性,研究成果为我国深部开采条件下的底板突水防治提供一定理论依据和参考价值。
(4)由于工作面底板地层分层分布特征,以及顶板断裂动载量化的差异性和动载作用的复杂性,导致理论模型计算结果与实际观测值存在一定的误差,今后的研究会进一步分析动载对承压含水层的影响,揭示底板承压水导升高度对动载扰动响应机制。
符号注释:
A为包括参数ρ、E、μ、ζ、s的矩阵;B、M、N为相关物理参数的集合运算;$ c $为黏聚力,MPa;d为动载作用范围,m;d1为工作面宽度,m;E为底板岩层弹性模量,MPa;E1为顶板弹性模量,MPa;f为任意函数;F为岩体破坏判断参数;G为剪切模量,Pa;$G = {E \mathord{\left/ {\vphantom {E {2\left( {1 + \mu } \right)}}} \right. } {2\left( {1 + \mu } \right)}}$;H为煤层底板埋深,m;h为底板深度(以工作面底界面为基准),m;h'为工作面底板到含水层距离,m;h1为破断岩层厚度,m;i为虚数单位;K为能量作用系数;K1、K2为支承压力应力集中系数;l为震源到采掘空间的距离。m;l1为支承压力降低区范围,m;l2、l3为支承压力增高区范围,m;L为初次垮落步距,m;p为承压含水层水压,MPa;q(t)为动载应力,MPa;q'为岩层自重和上覆岩层附加载荷的单位长度折算载荷,MPa;s为Laplace参数;t为时间,s;$ {t_1} $为动载作用时间,s;$u$为$x$方向位移,m;vf为围岩质点的峰值震动速度,m/s;$w$为${\textit{z}}$方向位移,m;x和z分别为水平和垂直方向;β为常数;$ \gamma $为底板上覆岩层容重,N/m3;$ {\sigma _0} $为动载幅值,MPa;$ {\sigma _x} $为水平应力,MPa;$ {\sigma _{\textit{z}}} $为垂直应力,MPa;$ {\tilde \sigma _{\textit{z}}} $为$ {\sigma _{\textit{z}}} $的Laplace变换结果,$ {\tilde \tau _{x{\textit{z}}}} $、$ \tilde u $、$ \tilde w $等类似;${\bar \sigma _{\textit{z}}} $为${\sigma _{\textit{z}}} $的Fourier变换结果,其他同;$ \varepsilon $为微元长度,m;ζ为动载传播速度,m/s;η为岩层破断时的地震效应;λ为动载衰减系数;$\mu $为泊松比;$\rho $为底板岩层密度,kg/m3;$\rho '$为煤岩介质密度,kg/m3;$ {\tau _{x{\textit{z}}}} $为剪应力,MPa;$ \varphi $为内摩擦角,(°);$ \omega $为动载频率,Hz。
-
表 1 各岩层物理力学参数
Table 1 Physical and mechanical parameters for various rock layers
岩层名称 弹性模量/
GPa泊松比 内摩擦
角/(°)黏聚力/
MPa抗拉强度/
MPa密度/
(kg·m−3)上覆岩层 30.79 0.27 35 2.6 2.8 2 500 泥岩1 23.50 0.28 33 2.2 1.8 2 570 粉砂岩1 18.01 0.25 26 2.8 1.7 2 650 8煤 13.08 0.23 23 1.2 0.8 1 620 细砂岩1 29.18 0.26 34 3.1 2.4 2 630 粉砂岩2 21.80 0.25 32 4.8 3.2 2 350 泥岩2 10.62 0.31 28 2.2 1.0 2 400 细砂岩2 21.75 0.29 32 2.6 1.3 2 380 中砂岩 18.50 0.25 34 4.5 2.8 2 700 粉砂岩3 20.33 0.21 31 3.8 2.5 2 680 泥岩3 8.21 0.35 35 2.1 2.9 2 650 灰岩 35.74 0.23 37 4.5 2.6 2 450 底部岩层 44.21 0.20 39 5.6 2.8 2 760 表 2 底板注水观测钻孔参数
Table 2 Parameters for observation boreholes in the floor
钻孔号 方位角/(°) 倾角/(°) 孔长/m 垂深/m 孔径/mm 1号 197 40 48 30 89 2号 197 51 38 30 89 3号 197 65 33 30 89 -
[1] 孙文洁,李文杰,宁殿艳,等. 我国煤矿水害事故现状、预测及防治建议[J]. 煤田地质与勘探,2023,51(12):185−194. SUN Wenjie,LI Wenjie,NING Dianyan,et al. Current states,prediction and prevention suggestions for water hazard accidents in China’s coal mines[J]. Coal Geology & Exploration,2023,51(12):185−194.
[2] 谢和平. “深部岩体力学与开采理论” 研究构想与预期成果展望[J]. 工程科学与技术,2017,49(2):1−16. XIE Heping. Research framework and anticipated results of deep rock mechanics and mining theory[J]. Advanced Engineering Sciences,2017,49(2):1−16.
[3] 董书宁,刘其声,王皓,等. 煤层底板水害超前区域治理理论框架与关键技术[J]. 煤田地质与勘探,2023,51(1):185−195. DONG Shuning,LIU Qisheng,WANG Hao,et al. Theoretical framework and key technology of advance regional control of water inrush in coal seam floor[J]. Coal Geology & Exploration,2023,51(1):185−195.
[4] 李昂,纪丙楠,牟谦,等. 深部煤岩层复合结构底板破坏机制及应用研究[J]. 岩石力学与工程学报,2022,41(3):559−572. LI Ang,JI Bingnan,MU Qian,et al. Failure mechanism of composite structure floors of deep coal and rock strata and its application[J]. Chinese Journal of Rock Mechanics and Engineering,2022,41(3):559−572.
[5] 曾一凡,武强,赵苏启,等. 我国煤矿水害事故特征、致因与防治对策[J]. 煤炭科学技术,2023,51(7):1−14. ZENG Yifan,WU Qiang,ZHAO Suqi,et al. Characteristics,causes,and prevention measures of coal mine water hazard accidents in China[J]. Coal Science and Technology,2023,51(7):1−14.
[6] 尹尚先,王屹,尹慧超,等. 深部底板奥灰薄灰突水机理及全时空防治技术[J]. 煤炭学报,2020,45(5):1855−1864. YIN Shangxian,WANG Yi,YIN Huichao,et al. Mechanism and full-time-space prevention and control technology of water inrush from Ordovician and thin limestone in deep mines[J]. Journal of China Coal Society,2020,45(5):1855−1864.
[7] 贾明魁. 坚硬顶板预裂对底板突水的影响[J]. 辽宁工程技术大学学报(自然科学版),2011,30(5):689−692. JIA Mingkui. Relationship between pre-cracking hard main roof and underground water ingress from floor at longwall face[J]. Journal of Liaoning Technical University (Natural Science),2011,30(5):689−692.
[8] 张西民,王秀辉. 顶板周期来压和底板突水的关系研究[J]. 煤田地质与勘探,1997,25(增刊1):51−53. ZHANG Ximin,WANG Xiuhui. The relationship of coal roof pressure and water-irruption from floor[J]. Coal Geology & Exploration,1997,25(Sup.1):51−53.
[9] 赵庆彪,蒋勤明,高春芳. 邯邢矿区深部煤层底板突水机理研究[J]. 煤炭科学技术,2016,44(3):117−121. ZHAO Qingbiao,JIANG Qinming,GAO Chunfang. Study on floor water inrush mechanism of deep seam in Hanxing Mining Area[J]. Coal Science and Technology,2016,44(3):117−121.
[10] LI Hailong,BAI Haibo. Simulation research on the mechanism of water inrush from fractured floor under the dynamic load induced by roof caving:Taking the Xinji second coal mine as an example[J]. Arabian Journal of Geosciences,2019,12(15):466. DOI: 10.1007/s12517-019-4621-8
[11] LI Chunyuan,ZUO Jianping,HUANG Xuanhao,et al. Water inrush modes through a thick aquifuge floor in a deep coal mine and appropriate control technology:A case study from Hebei,China[J]. Mine Water and the Environment,2022,41(4):954−969. DOI: 10.1007/s10230-022-00891-6
[12] 尹希文,于秋鸽,张玉军,等. 坚硬顶板厚隔水层条件下底板突水致灾机理及全周期治理技术[J]. 煤炭科学技术,2023,51(增刊1):318−327. YIN Xiwen,YU Qiuge,ZHANG Yujun,et al. Mechanism and whole cycle control technology of water inrush from coal seam floor on condition of hard roof and thick waterproof layer[J]. Coal Science and Technology,2023,51(Sup.1):318−327.
[13] 王朋朋. 深部高承压水上采动底板损伤破裂突水机理及控制研究[D]. 北京:中国矿业大学(北京),2022. WANG Pengpeng. Study on mechanism and control of water inrush from damaged and ruptured floor induced by mining disturbance and high water pressure in deep coal mining[D]. Beijing:China University of Mining and Technology (Beijing),2022.
[14] 李春元,张勇,张国军,等. 深部开采动力扰动下底板应力演化及裂隙扩展机制[J]. 岩土工程学报,2018,40(11):2031−2040. LI Chunyuan,ZHANG Yong,ZHANG Guojun,et al. Crack propagation mechanisms and stress evolution of floor under dynamic disturbance in deep coal mining[J]. Chinese Journal of Geotechnical Engineering,2018,40(11):2031−2040.
[15] 李春元,张勇,彭帅,等. 深部开采底板岩体卸荷损伤的强扰动危险性分析[J]. 岩土力学,2018,39(11):3957−3968. LI Chunyuan,ZHANG Yong,PENG Shuai,et al. Strong disturbance hazard analysis of unloading damage for floor rock mass in deep coal mining[J]. Rock and Soil Mechanics,2018,39(11):3957−3968.
[16] 李海龙,白海波,马丹,等. 采动底板导水破坏深度滞后煤壁二次加深规律探测[J]. 采矿与安全工程学报,2016,33(2):318−323. LI Hailong,BAI Haibo,MA Dan,et al. Experimental study on mining-induced failure depth lagging coal wall secondary deepening rule[J]. Journal of Mining & Safety Engineering,2016,33(2):318−323.
[17] 李春元,左建平,张勇. 深部开采底板破坏与基本顶岩梁初次垮断的联动效应[J]. 岩土力学,2021,42(12):3301−3314. LI Chunyuan,ZUO Jianping,ZHANG Yong. The linkage effect between floor failure and first weighting of the main roof in deep longwall mining[J]. Rock and Soil Mechanics,2021,42(12):3301−3314.
[18] 黄琪嵩,程久龙,丁厚成,等. 大范围顶板岩体垮落冲击动载对采场底板破坏的影响研究[J]. 采矿与安全工程学报,2019,36(6):1228−1233. HUANG Qisong,CHENG Jiulong,DING Houcheng,et al. Influence of impact load induced by large-scale roof caving on the failure characteristics of mining floor[J]. Journal of Mining & Safety Engineering,2019,36(6):1228−1233.
[19] ZHAO Xianwei,YANG Dengfeng,ZHU Yanyan,et al. Analysis on numerical simulation and fracture mechanics model of water inrush of floor with hidden faults under dynamic and static loads[J]. Frontiers in Earth Science,2024,12:1352992. DOI: 10.3389/feart.2024.1352992
[20] WANG Pengpeng,JIANG Yaodong,REN Qingshan. Roof hydraulic fracturing for preventing floor water inrush under multi aquifers and mining disturbance:A case study[J]. Energies,2022,15(3):1187. DOI: 10.3390/en15031187
[21] MU Zonglong,LIU Guangjian,YANG Jing,et al. Theoretical and numerical investigations of floor dynamic rupture:A case study in Zhaolou Coal Mine,China[J]. Safety Science,2019,114:1−11. DOI: 10.1016/j.ssci.2018.12.016
[22] 李浩,唐世斌,康志勤,等. 特厚煤层底板断层破坏与顶板垮断联动效应的CFDEM模拟研究[J]. 煤炭学报,2024,49(6):2615−2629. LI Hao,TANG Shibin,KANG Zhiqin,et al. CFDEM simulation on the linkage effect between floor faults failure and roof collapse in ultra-thick coal seam[J]. Journal of China Coal Society,2024,49(6):2615−2629.
[23] ZHAO Yanlin,LUO Shilin,WANG Yixian,et al. Numerical analysis of karst water inrush and a criterion for establishing the width of water-resistant rock pillars[J]. Mine Water and the Environment,2017,36(4):508−519. DOI: 10.1007/s10230-017-0438-4
[24] LI Chunyuan,ZUO Jianping,SHI Yue,et al. Deformation and fracture at floor area and the correlation with main roof breakage in deep longwall mining[J]. Natural Hazards,2021,107(2):1731−1755. DOI: 10.1007/s11069-021-04656-2
[25] 郝宪杰,李航,赵毅鑫,等. 基于日累积微震指标与水位关联效应的底板突水预警方法与应用[J]. 岩石力学与工程学报,2024,43(9):2125−2139. HAO Xianjie,LI Hang,ZHAO Yixin,et al. An early warning method and application of water inrush from coal mining floor based on the correlation effect between daily cumulative micro-seismic indicators and water level[J]. Chinese Journal of Rock Mechanics and Engineering,2024,43(9):2125−2139.
[26] 左宇军,李术才,秦泗凤,等. 动力扰动诱发承压水底板关键层失稳的突变理论研究[J]. 岩土力学,2010,31(8):2361−2366. ZUO Yujun,LI Shucai,QIN Sifeng,et al. A catastrophe model for floor water-resisting key stratum instability induced by dynamic disturbance[J]. Rock and Soil Mechanics,2010,31(8):2361−2366.
[27] 蔡武,窦林名,王桂峰,等. 煤层采掘活动引起断层活化的力学机制及其诱冲机理[J]. 采矿与安全工程学报,2019,36(6):1193−1202. CAI Wu,DOU Linming,WANG Guifeng,et al. Mechanism of fault reactivation and its induced coal burst caused by coal mining activities[J]. Journal of Mining & Safety Engineering,2019,36(6):1193−1202.
[28] 窦林名,何江,曹安业,等. 煤矿冲击矿压动静载叠加原理及其防治[J]. 煤炭学报,2015,40(7):1469−1476. DOU Linming,HE Jiang,CAO Anye,et al. Rock burst prevention methods based on theory of dynamic and static combined load induced in coal mine[J]. Journal of China Coal Society,2015,40(7):1469−1476.
[29] 赵洪宝,刘一洪,刘瑞,等. 卸荷扰动下窄煤柱巷道底板破坏力学行为分析[J]. 华中科技大学学报(自然科学版),2022,50(1):105−112. ZHAO Hongbao,LIU Yihong,LIU Rui,et al. Mechanical behavior analysis of floor failure of narrow coal pillar roadway under unloading disturbance[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition),2022,50(1):105−112.
[30] 朱斯陶,刘金海,姜福兴,等. 我国煤矿顶板运动型矿震及诱发灾害分类、预测与防控[J]. 煤炭学报,2022,47(2):807−816. ZHU Sitao,LIU Jinhai,JIANG Fuxing,et al. Classification,prediction,prevention and control of roof movement-type mine earthquakes and induced disasters in China’s coal mines[J]. Journal of China Coal Society,2022,47(2):807−816.
[31] 李文龙,屠世浩,郝定溢,等. 推采速度和充实率对深井充填面厚硬顶板聚能与释能的影响[J]. 中国矿业大学学报,2021,50(3):498−506. LI Wenlong,TU Shihao,HAO Dingyi,et al. Influence of mining speed and filling ratio on energy accumulation and release of thick and hard roof in deep backfilling working face[J]. Journal of China University of Mining & Technology,2021,50(3):498−506.
[32] 程辉,赵洪宝,张欢,等. 近距离煤层回采巷道底臌机理与防治技术研究[J]. 中南大学学报(自然科学版),2022,53(4):1392−1405. CHENG Hui,ZHAO Hongbao,ZHANG Huan,et al. Study on mechanism and prevention technology of floor heave of mining roadway in close distance coal seam[J]. Journal of Central South University (Science and Technology),2022,53(4):1392−1405.
[33] 张士川,郭惟嘉,孙文斌,等. 深部开采隐伏构造扩展活化及突水试验研究[J]. 岩土力学,2015,36(11):3111−3120. ZHANG Shichuan,GUO Weijia,SUN Wenbin,et al. Experimental research on extended activation and water inrush of concealed structure in deep mining[J]. Rock and Soil Mechanics,2015,36(11):3111−3120.
[34] 刘伟韬,宋文成,穆殿瑞,等. 底板采动破坏带分段观测系统与应用[J]. 中南大学学报(自然科学版),2017,48(10):2808−2816. LIU Weitao,SONG Wencheng,MU Dianrui,et al. Section observation system on floor mining damage zone and its application[J]. Journal of Central South University (Science and Technology),2017,48(10):2808−2816.
[35] YU Xiaoge,LIU Yifei,FAN Haibin. Influence of coal seam floor damage on floor damage depth[J]. Environmental Earth Sciences,2022,81(6):182. DOI: 10.1007/s12665-022-10315-x







 下载:
下载: