Rock bursts induced by thick-hard roof with compound key strata: Mechanisms and technical modes for prevention
-
摘要:目的
厚硬顶板是诱发煤矿冲击地压、矿震等灾害的关键因素，其中煤层顶板发育有复合关键层厚硬顶板条件下灾害更为严重，揭示复合关键层厚硬顶板诱冲机制，构建防治技术模式迫在眉睫。
方法运用物理相似模拟和力学分析等方法，建立复合关键层硬顶板和其非协同破断判识方法，揭示复合关键层厚硬顶板诱冲机制，优选防冲技术模式。
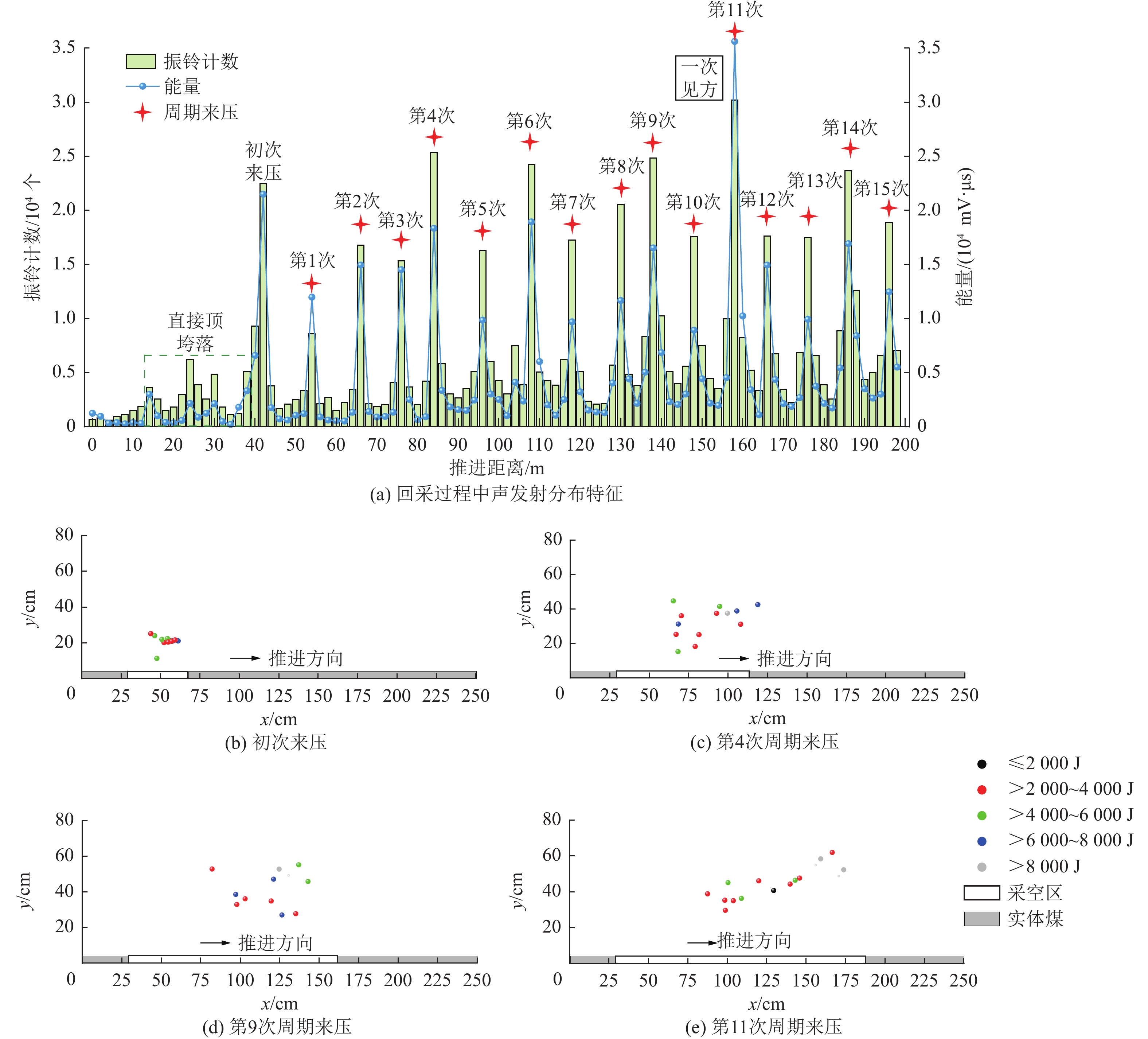
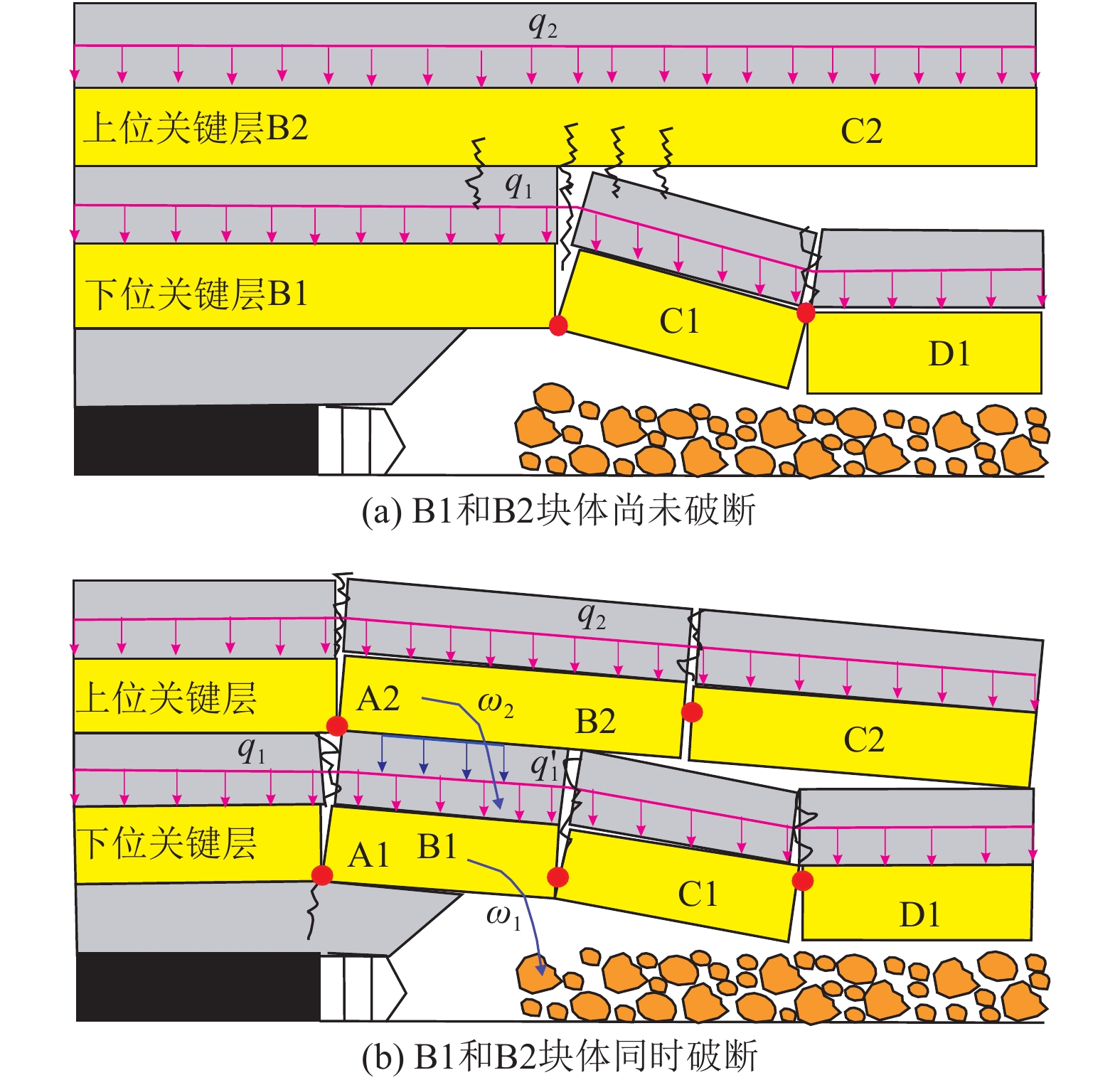
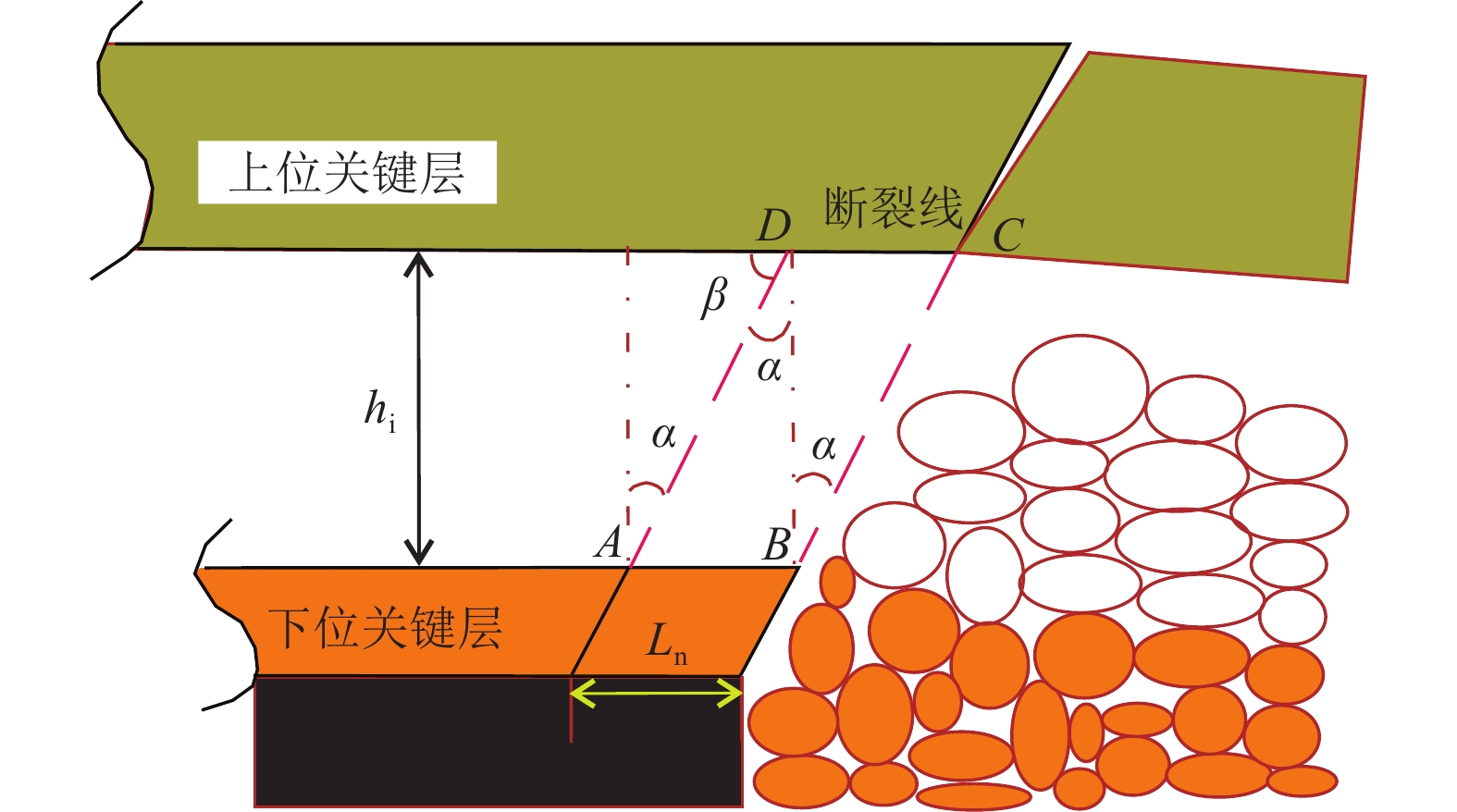
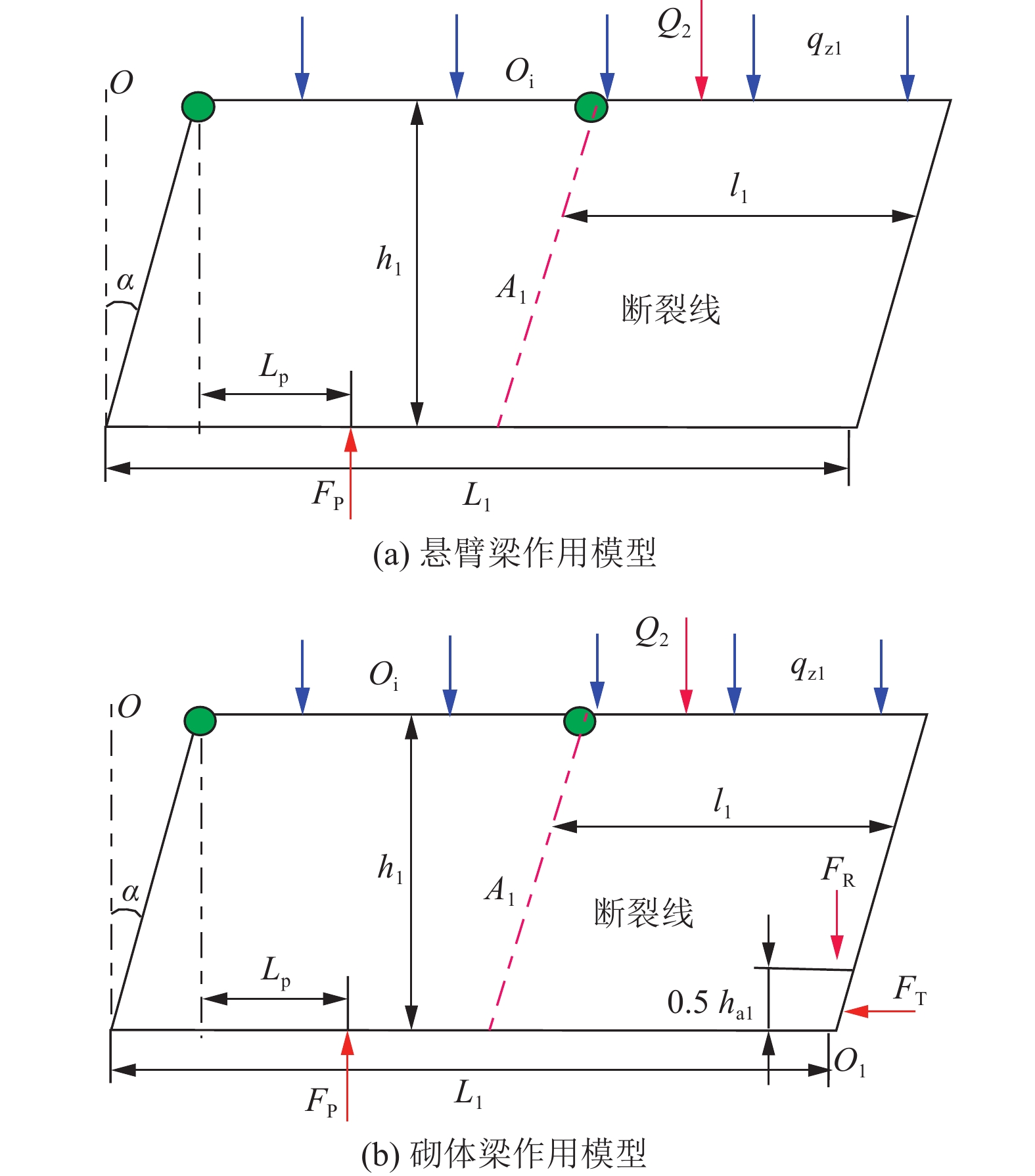
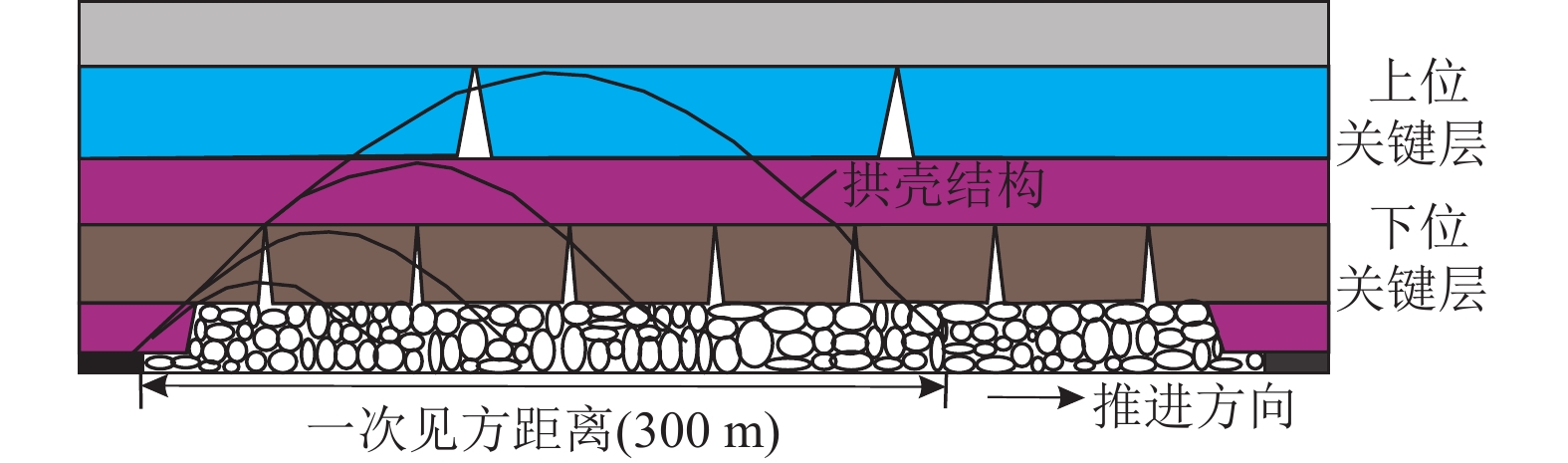
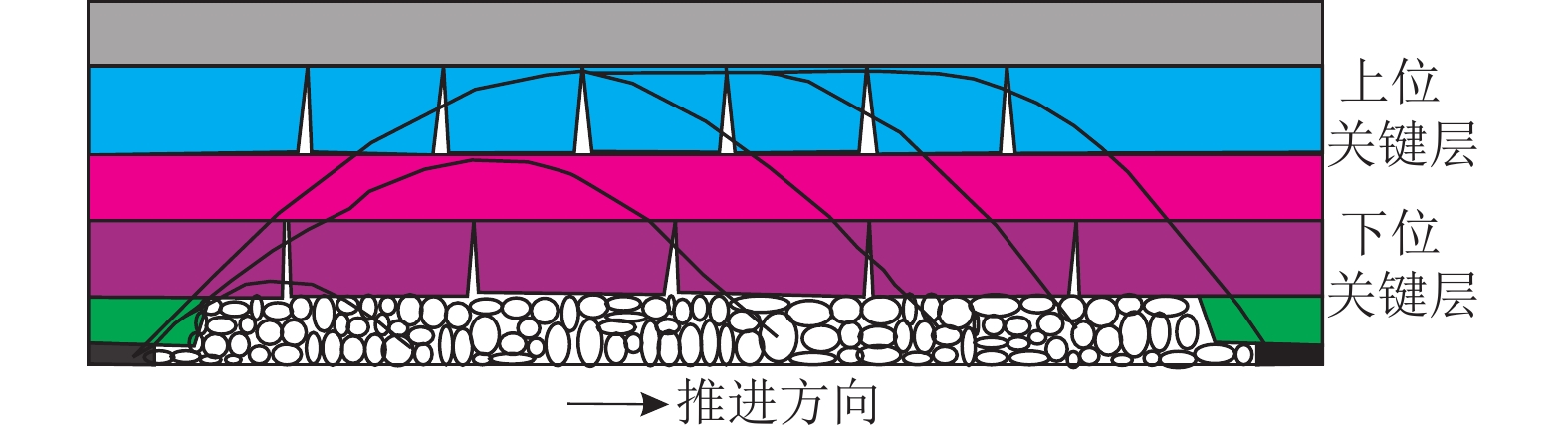
结果和结论结果表明：(1) 复合关键层厚硬顶板呈现“大−小”周期来压规律，来压期间声发射频次和微震能量分别为非来压的5.3倍与7.3倍；上、下位关键层厚硬顶板同步破断扰动叠加，叠合“周期”和“见方”来压效应诱发大型冲击地压灾害。(2) 建立了以中性轴线为基础的复合关键层判识模型，两层及以上关键层厚硬顶板形成复合关键层前提是梁模型横截面上剪切应力不超过对应的抗剪强度。(3) 形成了“悬臂梁”和“砌体梁”两种模式下合理破断线距离定量判识方法，提出了复合关键层厚硬顶板上、下单层和双层协同3种水力压裂卸压技术模式。(4) 分析显示下位关键层压裂主要改变了厚硬顶板关键层完整性和强度，缩短了来压步距，无法控制上位关键层“拱壳”结构大能量冲击地压；上位关键层压裂控制“大周期”破断扰动载荷，减弱了复合关键层耦合效应，大幅降低冲击地压危险性，是冲击地压主控层位，“上−下位”关键层协同压裂为最优卸压防冲模式。该研究成果将为复合厚硬顶板冲击地压地压、矿震灾害区域的精准防治提供重要依据。
Abstract:ObjectiveThick-hard roofs serve as the key factor inducing disasters such as rock bursts and mining-induced earthquakes in coal mines. These disasters are especially serious in the case of coal seam roofs with compound key strata. Hence, there is an urgent need to reveal the mechanisms behind the rock bursts induced by thick-hard roofs with compound key strata and to develop technical modes for the prevention and control of these rock bursts.
MethodsUsing methods including physical simulation experiments on similar materials and mechanical analysis, this study developed methods for identifying roofs with compound key strata and for non-synergistic breaking of the compound key strata. Furthermore, this study revealed the mechanism behind the rock bursts induced by the roof and selected the optimal technical mode for prevention. [Results and Conclusions] Key findings are as follows: (1) Thick-hard roof with compound key strata exhibited large and small periodic weighting, with acoustic emission frequency and microseismic energy during weighting being 5.3 and 7.3 times those in the absence of weighting. The synergistic breaking of the upper and lower compound key strata led to disturbance superimposition, with superimposed periodic effects and weighing effects at square locations inducting large-scale rock bursts. (2) An identification model of compound key strata based the neutral axis was established, revealing that the prerequisite for the phenomenon that two or more key strata in the thick-hard roof form compound key strata is that the shear stress on the cross-section does not exceed the corresponding shear strength in the beam model. (3) A method for quantitatively determining the distances of the breaking lines under the cantilever-beam and masonry-beam models was developed. Furthermore, three hydraulic fracturing and pressure relief technical modes were proposed: the fracturing of the upper key stratum, the fracturing of the lower key stratum, and the synergistic fracturing of both strata. (4) The results indicate that the fracturing of the lower key stratum primary, despite changing the integrity and strength of the lower key stratum and shortening the step distance in periodic weighting, failed to control the energetic rock bursts caused by the arched shells of the upper key stratum. The fracturing of the upper key stratum, the predominant layer influenced by rock bursts, controlled the loads induced by breaking disturbance in large weighing cycles, weakened the coupling effects between the compound key strata, and greatly reduced the dangerousness of rock bursts. In contrast, the synergistic fracturing of both strata was identified as the optimal mode for pressure relief and rock burst prevention. The results of this study will provide an important basis for the precise prevention and control of areas potentially struck by disasters such as rock bursts induced by thick-hard roofs with compound key strata and mining-induced earthquakes.
-
Keywords:
- thick-hard rock layer /
- rock burst /
- composite key layer /
- synergy /
- staged hydraulic fracturing
-
随着我国煤炭资源开采不断趋向深部，巷道掘进过程中频繁遭遇断层、破碎带等含水地质构造，对煤矿安全高效生产构成严峻的挑战[1]。矿井电法在巷道掘进水害超前探测中发挥着至关重要的作用，数十年来先后发展了巷道直流电超前探测[2]和聚焦扫描激电超前探测[3]等分支方法。两者在观测方法和原理方面存在显著差异，其中前者是在巷道掘进工作面后方沿轴向布置多个点电源和接收电极，观测岩层视电阻率的分布特征，据此评价巷道掘进前方岩层的富水性[4-5]；后者是在地表隧道聚焦电流方法[6]的基础上，由时域直流供电改为频域交流供电变换而来，主要是在掘进工作面以特定形式布置发射电极组，实现电流聚焦发射，以此观测掘进前方岩层的视频散率等激电参数分布特征来预测预报岩层富水性[7-10]。与后者相比，前者在探测理论[11-22]、观测与解释方法[23-31]等方面发展较为成熟，取得了大量的研究成果，具有探测距离远、可操作性强等技术优势，仍是目前实际巷道超前探测广泛采用的工作方法。但大量实践表明，巷道直流电超前探测方法现阶段仍存在两个方面的不足。其一是该方法以视电阻率低值异常作为岩层富水评价的依据，而视电阻率低值异常的致因复杂，多解性强，实际探测易出现误报和多报等问题；其二是该方法数据采集主要沿巷道掘进后方轴向布置，所获得的探测结果缺乏对含水体方位的判识能力，导致实际探测精度偏低。
为弥补上述不足，鉴于频率域激电可获取视复电阻率和视频散率等激电视参数，综合解释能有效降低电性异常多解性[32]，笔者拟提出巷道三方向激电视参数观测方法，并以板状含水体为研究对象，采用公式推导、数值计算及理论分析等方法探究巷道内激电视参数的响应特征及其各向异性，掌握三方向激电视参数与板体产状参数之间的敏感特性，为更好判识巷道掘进前方含水体方位提供依据。
1 三方向激电视参数观测方法
鉴于常规电法超前观测方式因沿巷道掘进后方轴向(图1中x轴负方向)布置电极而导致对前方含水体的响应信息捕捉能力不足，提出三方向激电视参数观测方法，该方法主要通过观测巷道掘进前方岩层视复电阻率和视频散率来探测巷道掘进前方含水异常分布情况。具体观测步骤如下所述。
![]()
图 1 三方向观测系统1—巷道掘进前方；2—巷道掘进工作面；3—巷道底板；4—供电电缆；5—电法仪；6—供电正极；7—供电点切换开关；8—巷道掘进后方；9—接收电缆；10—测量点；11—三方向测量电极组；12—供电负极；13—巷道侧帮Figure 1. Triaxial observation system(1)如图1所示，在巷道侧帮与底板交线上沿掘进后方(x轴负方向)布置电法测线，以坐标系原点O作为测线起点A1，向掘进后方依次布置w个供电点和n个测量点，每个测量点布置1个三方向测量电极组，每个电极组由M、Nx、Ny和Nz共4个电极组成，实际中应尽量保证MNx、MNy、MNz相互正交且间距相等。第二个测量点的M电极是第一个测量点的Nx电极，依此类推。同时在巷道掘进后方布置无穷远电极B，通过仪器与供电电缆将所有电极连成完整供电测量回路。
(2)依次在每个供电点分别供入低频fd和高频fg电流，并记录供电电流I；供电同时，同步测量每个测点的MNx、MNy和MNz共3个方向的交流电位差$ \Delta {U_{{{MN}}}}({f_{\text{d}}}) $和$ \Delta {U_{{{MN}}}}({f_{\text{g}}}) $。然后根据下式计算所有测点的三方向视复电阻率$ {\rho _{\text{s}}}(f) $和视频散率$ {\mathrm{PFE}}({f_{\text{d}}},{f_{\mathrm{g}}}) $，据此分析地电异常体的分布特征。
$$ \left\{ \begin{aligned} & {{\rho _{\text{s}}}(f) = \frac{{4{\text{π }} \cdot AM \cdot AN}}{{AN - AM}}\cdot \frac{{\Delta {U_{{{MN}}}}(f)}}{I}} \\ & {{\mathrm{PFE}}({f_{\text{d}}},{f_{\mathrm{g}}}) = \frac{{{\rho _{\text{s}}}({f_{\text{d}}}) - {\rho _{\text{s}}}({f_{\text{g}}})}}{{{\rho _{\text{s}}}({f_{\text{g}}})}} \times 100\text{%} } \end{aligned}\right. $$ (1) 2 板状体三方向激电视参数公式
针对断层等含水异常体，此处以无限大板状良导体为模型。如图2所示，假设电阻率ρ1的全空间均匀介质中有一厚度a、电阻率ρ2的无限大板状体。若空间中任意点A供交流电，且A点至板体的垂直距离为d，则可知全空间可划分为板体ρ2介质区、有源ρ1介质区和无源ρ1介质区。由于观测点位于有源ρ1介质区中，为便于推导任意点P的电位表达式，首先讨论板状体直立情况(图2a)。以A为坐标原点，则P点电位分布关于x轴对称，选取柱坐标系，电位函数方程可简化为：
![]()
图 2 全空间中大板状体观测系统Figure 2. Observation system for an infinitely large tabular body in the whole space$$ \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial U}}{{\partial r}}} \right) + \frac{\partial }{{\partial x}}\left( {r\frac{{\partial U}}{{\partial x}}} \right) = 0 $$ (2) 此式的一般解为：
$$ U = \int\limits_0^\infty {\left[ {A\left( m \right){{\mathrm{exp}}({ - mx})} + B\left( m \right){{\mathrm{exp}}({mx})}} \right]} \times {J_0}\left( {mr} \right){\text{d}}m $$ (3) 结合介质分界面处电位和电流密度的法向分量连续边界条件，可推导点P的电位表达式为：
$$ \begin{aligned} &{U_{{P}}} = \frac{{I{\rho _1}}}{{4\pi }} \times \left\{ \frac{1}{{{R_{{P}}}}} - \left[ \sum\limits_{n = 1}^\infty \frac{{{{[({\rho _2} - {\rho _1})/({\rho _2} + {\rho _1})]}^{2n - 1}}}}{{\sqrt {{r^2} + {{\left( {2na + 2d - x} \right)}^2}} }} -\right.\right.\\ &\qquad \left.\left.\sum\limits_{n = 1}^\infty {\frac{{{{[({\rho _2} - {\rho _1})/({\rho _2} + {\rho _1})]}^{2n - 1}}}}{{\sqrt {{r^2} + {{\left( {2na + 2d - 2a - x} \right)}^2}} }}} \right] \right\}\end{aligned} $$ (4) 其次，在板体存在倾角θ和方位角φ时(图2b)，可对原坐标系进行坐标变换，再考虑电流的交变性，可进一步获得任意点M、Nx、Ny、Nz的复电位表达式，具体见下式：
$$ \left\{ \begin{aligned} & {U_{{M}}}({\text{i}}\omega ) = \frac{{I{\rho _1}({\text{i}}\omega )}}{{4\pi }} \times \\ &\qquad \left\{ {\frac{1}{{{R_{{M}}}}} - \left[ {\sum\limits_{{{n}} = 1}^\infty {\frac{{{{\left\{ {{{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} \mathord{\left/ {\vphantom {{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right. } {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right\}}^{2{{n}} - 1}}}}{{\sqrt {{X_0} + {{\left( {2{\text{n}}a + 2d - {x_{{M}}}\sin \theta \cos \varphi } \right)}^2}} }}} - \sum\limits_{{{n}} = 1}^\infty {\frac{{{{\left\{ {{{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} \mathord{\left/ {\vphantom {{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right. } {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right\}}^{2{{n}} - 1}}}}{{\sqrt {{X_0} + {{\left( {2{{n}}a + 2d - 2a - {x_{{M}}}\sin \theta \cos \varphi } \right)}^2}} }}} } \right]} \right\} \\ & {U_{{{Nx}}}}({\text{i}}\omega ) = \frac{{I{\rho _1}({\text{i}}\omega )}}{{4\pi }} \times \\ &\qquad \left\{ {\frac{1}{{{R_{{{Nx}}}}}} - \left[ {\sum\limits_{{{n}} = 1}^\infty {\frac{{{{\left\{ {{{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} \mathord{\left/ {\vphantom {{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right. } {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right\}}^{2{{n}} - 1}}}}{{\sqrt {{Y_0} + {{\left[ {2{{n}}a + 2d - \left( {{x_{{M}}} - s} \right)\sin \theta \cos \varphi } \right]}^2}} }}} - \sum\limits_{{{n}} = 1}^\infty {\frac{{{{\left\{ {{{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} \mathord{\left/ {\vphantom {{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right. } {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right\}}^{2{{n}} - 1}}}}{{\sqrt {{Y_0} + {{\left[ {2{{n}}a + 2d + 2a - \left( {{x_{{M}}} - s} \right)\sin \theta \cos \varphi } \right]}^2}} }}} } \right]} \right\} \\ & {U_{{{Ny}}}}({\text{i}}\omega ) = \frac{{I{\rho _1}({\text{i}}\omega )}}{{4\pi }} \times \\ &\qquad \left\{ {\frac{1}{{{R_{{{Ny}}}}}} - \left[ {\sum\limits_{{{n}} = 1}^\infty {\frac{{{{\left\{ {{{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} \mathord{\left/ {\vphantom {{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right. } {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right\}}^{2{{n}} - 1}}}}{{\sqrt {{Z_0} + {{\left[ {2{{n}}a + 2d - \left( {{x_{{M}}}\sin \theta \cos \varphi + s\sin \theta \sin \varphi } \right)} \right]}^2}} }}} - \sum\limits_{{{n}} = 1}^\infty {\frac{{{{\left\{ {{{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} \mathord{\left/ {\vphantom {{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right. } {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right\}}^{2{{n}} - 1}}}}{{\sqrt {{Z_0} + {{\left[ {2{{n}}a + 2d + 2a - \left( {{x_{{M}}}\sin \theta \cos \varphi + s\sin \theta \sin \varphi } \right)} \right]}^2}} }}} } \right]} \right\} \\ & {U_{{{N{\textit{z}}}}}}({\text{i}}\omega ) = \frac{{I{\rho _1}({\text{i}}\omega )}}{{4\pi }} \times \\ &\qquad \left\{ {\frac{1}{{{R_{{{N{\textit{z}}}}}}}} - \left[ {\sum\limits_{{{n}} = 1}^\infty {\frac{{{{\left\{ {{{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} \mathord{\left/ {\vphantom {{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right. } {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right\}}^{2{{n}} - 1}}}}{{\sqrt {{W_0} + {{\left[ {2{{n}}a + 2d - \left( {{x_{{M}}}\sin \theta \cos \varphi + s\cos \theta } \right)} \right]}^2}} }}} - \sum\limits_{{{n}} = 1}^\infty {\frac{{{{\left\{ {{{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} \mathord{\left/ {\vphantom {{\left[ {{\rho _2}({\text{i}}\omega ) - {\rho _1}({\text{i}}\omega )} \right]} {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right. } {\left[ {{\rho _2}({\text{i}}\omega ) + {\rho _1}({\text{i}}\omega )} \right]}}} \right\}}^{2{{n}} - 1}}}}{{\sqrt {{W_0} + {{\left[ {2{{n}}a + 2d + 2a - \left( {{x_{{M}}}\sin \theta \cos \varphi + s\cos \theta } \right)} \right]}^2}} }}} } \right]} \right\} \end{aligned} \right. $$ (5) 其中，$ {W_0} = {\left( {{x_{{M}}}\sin \varphi } \right)^2} + {\left( {{x_{{M}}}\cos \theta \cos \varphi - s\sin \theta } \right)^2} $，$ {X_0} = x_{{M}}^2\left( {{{\sin }^2}\varphi + {{\cos }^2}\theta {{\cos }^2}\varphi } \right) $，$ {Y_0} = {\left( {{x_{{M}}} - s} \right)^2}\left( {{{\sin }^2}\varphi + {{\cos }^2}\theta {{\cos }^2}\varphi } \right) $，$ {Z_0} = {\left( { - {x_{{M}}}\sin \varphi + s\cos \varphi } \right)^2} + {\left( {{x_{{M}}}\cos \theta \cos \varphi + s\cos \theta \sin \varphi } \right)^2} $。
目前，常用Cole-Cole模型来描述岩石的激电效应，则交流电场作用下岩石的复电阻率$ {\rho _{\text{s}}}(f) $可写为：
$$ {\rho _{\text{s}}}(f) = {\rho _0}\left\{ {1 - m\left[ {1 - \frac{1}{{1 + {{({\text{i}}\omega \tau )}^c}}}} \right]} \right\} $$ (6) 因此，在求解式(5)时，其中ρ1(iω)和ρ2(iω)可依据式(6)求得，再结合式(1)分别计算出高频和低频电流作用下的三方向激电视参数，包括MNx、MNy和MNz 3个方向的视频散率PFE(x)、PFE(y)和PFE(z)以及不同频率电流供电下的视复电阻率值ρs(x)、ρs(y)和ρs(z)。
3 三方向激电视参数响应特征
3.1 模型参数设置
矿井电法超前探测的对象主要是含水体，结合实际观测条件，此处令ρ1=100 Ω·m、c1=0.3，τ1=0.1 s、m1=0.015、ρ2=10 Ω·m、c2=0.3、τ2=0.5 s、m2=0.3，a=5 m，s=2 m，fd=8 Hz，fg=128 Hz，并从供电点沿巷道后方依次布置64个三方向测量电极组，相邻电极组间距设为2 m，控制测量长度为126 m。通过设置不同板状体模型参数(表1)，分析三方向激电视参数随方位角φ、倾角θ及板体至场源距离d的变化规律。
表 1 不同产状的板状体地电模型Table 1. Geoelectric models of tabular bodies with different attitudes模型编号 倾角θ/(°) 方位角φ/(°) 距离d/m Model1 30 −90~90 10 Model2 60 −90~90 10 Model3 90 −90~90 10 Model4 120 −90~90 10 Model5 150 −90~90 10 Model6 30~150 0 10 Model7 30~150 30 10 Model8 30~150 60 10 Model9 30~150 90 10 Model10 30 0 5~30 Model11 60 30 5~30 Model12 90 30 5~30 3.2 激电视参数随方位角变化的响应特征
巷道掘进前方的断层等近似板状体，在方位上可能位于巷道左前方(0°<φ≤90°)、正前方(φ=0°)和右前方(−90°≤φ<0°)，在倾向上可能有沿巷道掘进前方(0°≤θ<90°)、处于直立状态(θ=90°)和沿巷道掘进后方(90°<θ≤180°)3种情况；在分析激电视参数随φ变化的响应特征时，需同时考虑θ的影响，故此处设置5种不同模型(表1中Model1—Model5)在不同φ情况下的三方向视频散率曲线，如图3所示。
![]()
图 3 不同φ对应的三方向视频散率曲线注：30°与−30°，60与−60°，90°与−90°时曲线重合。Figure 3. Triaxial frequency dispersivity curves under different φ values由图3可知：(1)当0°<φ≤90°和−90°≤φ<0°时，在$ \left| \varphi \right| $相同情况下，PFE(x)、PFE(y)和PFE(z)曲线重叠。(2)各模型对应的PFE(x)均为K型曲线(低−高−低)，随模型从巷道正前方偏向巷道左前方(0°<φ≤90°)或右前方(−90°≤φ<0°)，PFE(x)曲线极大值异常幅度增大，极值点位置向场源A靠近，即探测极距$ \left| {AM} \right| $逐渐减小；如当θ=30°(图3a)、60°(图3b)、90°(图3c)时，随φ从0°增大至90°或从0°减小至−90°，PFE(x)曲线极大值分别从1.390 2%、1.206 4%、1.161 4%增大至1.968 2%，对应的AM分别从−78、−96、−104 m偏移至−58 m。(3)各模型对应的PFE(y)曲线随φ发生变化。当φ≠0°时，PFE(y)曲线呈现反比例函数型特征，存在阶跃点，且随模型不断偏向巷道左帮(φ→90°)或右帮(φ→−90°)，阶跃点位置不断向场源靠近；如当θ=30°、60°、90°时，随φ从0°增大至90°或从0°减小至−90°，阶跃点对应的AM位置分别从−58、−66、−68偏移至−50 m。当φ=0°时，PFE(y)曲线幅值均较小且表现出K型变化规律。(4)在θ≠90°情况下，各模型对应的PFE(z)曲线同样表现为反比例函数型特征，存在阶跃点，PFE(z)曲线随φ变化的规律与PFE(y)曲线一致；而当θ=90°时，PFE(z)曲线表现为K型，随φ变化的规律与PFE(x)曲线相似。
图4为Model1在供电流8 Hz时的三方向视复电阻率响应曲线。由图4可知：(1)在0°<φ≤90°和−90°≤φ<0°时，在$ \left| \varphi \right| $相同情况下，ρs(x)和ρs(z)曲线重叠，而ρs(y) 曲线则表现对称性，这与PFE(y)曲线表现特征不同。(2) ρs(x)曲线表现为H型(即高−低−高)，随模型从巷道正前方偏向巷道两帮，曲线极小值异常幅度增大，极小值点位置逐渐靠近场源，如φ=0°、30°、60°、90°时，AM分别为−52、−50、−46和−40 m；与图3a中PFE(x)曲线极值位置(φ=0°、30°、60°、90°时，AM分别为−78、−74、−66和−58 m)相比，ρs(x)曲线极小值更接近场源，且随模型从正前方偏向两帮，极值位置的变化相对较小。(3) ρs(y)曲线在(0°<φ≤90°)时表现出K型变化规律，随模型越趋向巷道左前方，曲线极大值逐渐增大，对应的AM位置总体位于−28 m附近；在(−90°≤φ≤0°)时表现出H型变化规律，随断层越偏向巷道右前方，曲线极小值逐渐减小，对应的AM位置约位于−30 m处；可见，与PFE(y)相比，ρs(y)曲线极值的AM位置随方位变化较小。(4)随模型从巷道正前方偏向巷道两帮，ρs(z)曲线极大值异常幅度增大且其位置向场源靠近，曲线极大值对应的AM位置总体位于−28 m附近；与PFE(z)相比，ρs(z)曲线极值位置随方位变化同样较小。其他模型的三方向视复电阻率曲线与Model1类似，限于篇幅，此处不再赘述。
![]()
图 4 Model1的8 Hz三方向视复电阻率曲线Figure 4. Triaxial apparent complex resistivity curves of Model1 under 8 Hz以上分析表明，三方向激电视参数曲线的异常极值及其探测极距随模型方位的变化而变化，其中x方向始终表现“低阻高频散”异常，y和z方向则存在极值和阶跃异常两种情况。但PFE(x)、PFE(z)、ρs(x)、ρs(z)曲线的形态不变，难以分辨模型方位。依据PFE(y)曲线形态特征可确定模型是否处于巷道正前方，ρs(y)曲线形态可辨别模型是位于巷道左前方或右前方，但前者极值位置随方位变化的幅度更大，对模型方位更为敏感。
3.3 激电视参数随倾角变化的响应特征
依据上文分析，异常体模型方位在巷道左前方或右前方时，三方向视频散率曲线在$ \left| \varphi \right| $相同情况下重叠，故此处设置模型位于巷道左前方(0°<φ≤90°)或正前方(φ=0°)两种场景，共4种不同地电模型(表1中Model6—Model9)，在不同倾角情况下的三方向视频散率曲线，如图5所示。
![]()
图 5 不同θ对应的三方向视频散率曲线Figure 5. Triaxial apparent frequency dispersivity curves under different θ values由图5可知：(1)在0°≤θ<90°和90°<θ≤180°情况下，PFE(x)、PFE(y)和PFE(z)曲线在$ \left| \theta \right| $相同情况下重叠，尤其是当模型位于巷道两帮(φ→90°或φ→−90°)时，所有倾角情况下的PFE(x)、PFE(y)曲线均重叠，不再随θ变化而变化(图5d)。(2)各模型对应的PFE(x)曲线均表现为K型，随模型从直立倾向巷道前方(0°≤θ<90°)或后方(90°<θ≤180°)，PFE(x)曲线极大值异常幅度增大且极值位置向场源A靠近；如当φ=0°(图5a)、30°(图5b)、60°(图5c)时，随θ从90°变化至30°(即模型倾向从直立变化至巷道掘进前方)，PFE(x)曲线极大值分别从1.161 4%、1.206 4%、1.390 2%增大至1.390 2%、1.437 9%、1.603 4%，对应的AM分别从−106、−96、−78 m偏移至−78、−74、−66 m。(3)各模型的PFE(y)曲线随θ变化而变化，受方位角φ影响，变化规律不一致。如当φ≠0°时，PFE(y)曲线呈现反比例函数分布特征，存在阶跃点，且随模型不断趋于平缓(θ→0°或θ→180°)，阶跃点位置越趋向于场源(φ=90°除外，图5d)；而当φ=0°时，PFE(y)曲线表现为K型(图5a)，随θ的变化特征与PFE(x)类似。(4)在θ≠90°情况下，各模型对应的PFE(z)曲线同样表现为反比例函数型特征，PFE(z)曲线随θ变化的规律与PFE(y)曲线一致；而当θ=90°时，PFE(z)曲线表现为K型。
图6给出了Model7模型在供8 Hz电流时的三方向视复电阻率响应曲线。由图6可知：(1)在0°≤θ<90°和90°<θ≤180°情况下，$ \left| \theta \right| $相同的ρs(x)、ρs(y)曲线重叠，而ρs(z)曲线则表现对称性。这与PFE(z)曲线特征不同。(2) ρs(x)曲线表现为H型，随模型从直立倾向巷道前方或后方，曲线极小值异常幅度增大，对应的AM位置逐渐靠近场源，如θ=90°、120°、150°时，AM分别为−64、−60、和−50 m；与图5b中PFE(x)曲线极值位置(θ=90°、120°、150°时，AM分别为−96、−90和−74 m)相比，ρs(x)曲线极小值更接近场源，且随模型从直立倾向巷道前方或后方，极值位置的变化相对较小。(3)随模型从直立倾向巷道前方或后方，ρs(y)曲线极大值异常幅度减小且其位置向场源靠近，曲线极大值对应的AM位置总体位于−28 m附近；与PFE(y)相比，ρs(y)曲线极值位置随倾角变化较小。(4) ρs(z)曲线在(0°≤θ<90°)时表现出K型变化规律，随模型倾向巷道前方，曲线极大值逐渐增大，对应的AM位置总体位于−28 m附近；在(90°<θ≤180°)时表现出H型变化规律，随模型倾向巷道后方，曲线极小值逐渐减小，对应的AM总体位于−32 m处。与PFE(z)相比，ρs(z)曲线极值位置随倾角变化同样较小。其他模型的三方向视复电阻率曲线与Model7类似，此处不再赘述。
![]()
图 6 Model7的8 Hz三方向视复电阻率曲线Figure 6. Triaxial apparent complex resistivity curves of Model7 under 8 Hz以上分析表明，三方向激电视参数的异常极值及其AM位置随模型倾角的变化而变化，其中x方向始终表现“低阻高频散”异常，y和z方向存在极值和阶跃异常两种情况。但PFE(x)、PFE(y)、ρs(x)、ρs(y)曲线的形态不变，无法据此分辨模型倾向。依据PFE(z)曲线形态特征可确定模型是否处于直立状态，ρs(z)曲线形态可辨别模型是前倾还是后倾，但前者极值位置随倾角变化的幅度更大，对模型倾角更为敏感。
3.4 激电视参数随距离变化的响应特征
图7给出了Model10—Model12在不同d时的三方向视频散率曲线。由图7可知：(1)三方向视频散率曲线形态不随模型距离d的变化而变化。(2)在模型处于不同方位和倾角时，随距离d增大，PFE(x)曲线极大值减小且对应的AM位置逐渐远离场源。如Model10随d从5 m增大至20 m，PFE(x)极大值分别从1.783%减小至
1.0432 %，对应的AM从−52 m偏移至−118 m；d≥25 m时，极值点对应的AM超过巷道后方观测范围；Model11和Model12随d增大，PFE(x)的极值异常及其AM位置变化情况与Model10类似。(3)由于方位角的差异，PFE(y)曲线形态存在K型(φ=0°)和反比例函数型(φ≠0°)两种情况，前者存在极值点，后者存在阶跃点。随d增大，极值点和阶跃点的位置均不断远离场源。如Model10随d从5 m增大至20 m，极值点对应的AM位置从−68 m偏移至−126 m；Model11和Model12随d从5 m增大至20 m，阶跃点AM位置分别从−40、−42 m偏移至−110、−114 m。(4)由于倾角的差异，PFE(z)曲线形态同样有K型(θ=90°)和反比例函数型(θ≠90°)两种变化规律，极值点和阶跃点随距离d的变化特征与PFE(y)变化特征基本一致。![]()
图 7 不同d对应的三方向视频散率曲线Figure 7. Triaxial apparent frequency dispersivity curves under different d values图8为Model11在8 Hz电流供电时的三方向视复电阻率响应曲线。由图8可知：(1)随d增大，ρs(x)曲线表现为H型，ρs(y)和ρs(z)曲线表现K型，各曲线形态不随d变化而变化。(2)随d增大，ρs(x)曲线极小值增大(即异常幅度减小)，对应的AM位置逐渐远离场源，如d从5 m增大至20 m，AM从−44 m偏移至−114 m；当d≥25 m时，探测极距|AM|>128 m；与之不同，ρs(y)和ρs(z)曲线极值异常幅度随d增加而增大，但对应的AM位置逐渐远离场源，如d从5 m增大至20 m，ρs(y)曲线的极大值对应的AM从−20 m偏移至−80 m，ρs(z)极大值对应的AM位置从−20 m偏移至−82 m。其他模型与Model11情况类似，不再赘述。
![]()
图 8 Model11的8 Hz三方向视复电阻率曲线Figure 8. Triaxial apparent complex resistivity curves of Model11 under 8 Hz以上分析表明，模型距离不改变三方向激电视参数曲线的形态特征，但对异常幅度及探测极距有较大影响。其中x方向仍为“低阻高频散”异常，异常幅度总体随距离增大而减小；y和z方向存在极值和阶跃异常两种情况，极值点或阶跃点对应的AM位置随距离增大逐渐远离场源。可见，模型距离的变化对辨识异常体的方位影响较小。
4 结 论
(1) 基于频域率电法建立了巷道掘进三方向激电视参数超前观测方法，该方法能有效捕捉巷道前方的地电信息，提高对含水异常体方位的判识精度。
(2) 通过理论推导和数值计算，分析了激电视参数随模型方位角、倾角及距离的响应特征：巷道轴向的激电视参数对模型产状的敏感性较差，而垂直巷道两帮的激电视参数对模型方位敏感，垂直巷道顶底板方向的激电视参数对模型倾向敏感。
(3) 三方向激电视参数的异常幅值及其探测极距显著受到模型参数的影响，尤其是异常极值点或阶跃点对应的探测极距，随模型至场源距离的变化而发生显著变化。
(4) 本次构建的含水体模型简单，对三方向激电视参数响应特征认知存在一定局限，需结合多种地电条件深入研究。同时，巷道掘进地质条件复杂，需发展综合超前探测，并进一步研究联合反演与解释。
符号注释：
a为板状体模型厚度，m；AM为场源与M点的间距，即探测极距，m；AN为场源与N点的间距，m；A(m)、B(m)为过程函数；c为频率相关因数，c1和c2分别为均匀介质和板状体模型的频率相关因数；d为板状体模型与供电场源的垂直距离，m；f为供电电流频率、fd和fg分别为低频和高频电流的频率，Hz；I为供电电流大小，A；J0为零阶贝塞尔函数；m为充电率，m1和m2分别为均匀介质和板状体模型的充电率；PFE为视频散率，%；r为图2a中M点与任意点P点间的距离，m；RM、RNx、RNy、RNz和RP分别为图2中A至M、Nx、Ny、Nz和任意点P的距离，m；s为测量点间距，m；U为电位值、UP为任意点P的电位值，V；$ {U_{{M}}}({\text{i}}\omega ) $、$ {U_{{{Nx}}}}({\text{i}}\omega ) $、$ {U_{{{Ny}}}}({\text{i}}\omega ) $和$ {U_{{{N{\textit{z}}}}}}({\text{i}}\omega ) $分别为M、Nx、Ny、Nz点的复电位值，V；$ \Delta {{{U}}_{{{MN}}}}({f_{\text{g}}}) $，$ \Delta {{{U}}_{{{MN}}}}({f_{\text{d}}}) $分别为点M、N间的高频电位差和低频电位差，V；xM为图2中M点的x坐标；W0、X0、Y0、Z0为用于简化公式表达的引入符号；θ为板状体模型倾角，(°)；τ为时间常数、τ1和τ2分别为均匀介质和板状体模型的时间常数，s；φ为板状体模型方位角，(°)；ρ0、ρ1、ρ2分别为零频电阻率、全空间均匀介质电阻率和板状体模型电阻率，Ω·m；ρs(f)为视复电阻率，Ω·m；ρ1(iω)和ρ2(iω)分别为全空间均匀介质和板状体模型的复电阻率，Ω·m；ω=2πf为角频率，Hz。
-
![]()
图 1 复合关键层厚硬顶板分析模型
Fig. 1 Model for the analysis of a thick-hard roof with composite key strata
![]()
图 3 复合关键层覆岩运移物理模型
Fig. 3 Physical model illustrating the migration of overlying compound key strata
![]()
图 4 复合关键层厚硬顶板破断特征
Fig. 4 Breaking characteristics of the roof with compound key strata
![]()
图 5 模型回采过程中声发射及微震能量变化
Fig. 5 Changes in acoustic emission frequency and microseismic energy during the mining of model
![]()
图 6 复合关键层厚硬顶板同时破断
Fig. 6 Concurrent breaking of composite key strata in the thick-hard roof
![]()
图 7 “上−下”位复合关键层无相互扰动模型
Fig. 7 Model illustrating the absence of mutual disturbance between the upper and lower compound key strata
![]()
图 8 “上−下”位复合关键层无相互扰动模型
Fig. 8 Models illustrating the absence of mutual disturbance between the upper and lower compound key strata
![]()
图 9 复合关键层井下分段压裂弱化模式
Fig. 9 Downhole staged fracturing mode of composite key strata for weakening breaking
![]()
图 10 下位关键层压裂后顶板“拱壳”结构
Fig. 10 Arched shells of the roof formed after the fracturing of the lower key stratum
![]()
图 11 上位关键层压裂后顶板“拱壳”结构
Fig. 11 Arched shells of the roof formed after the fracturing of the upper key stratum
![]()
图 12 复合关键层协同压裂破断结构
Fig. 12 Breaking structures caused by synergistic fracturing of compound key strata
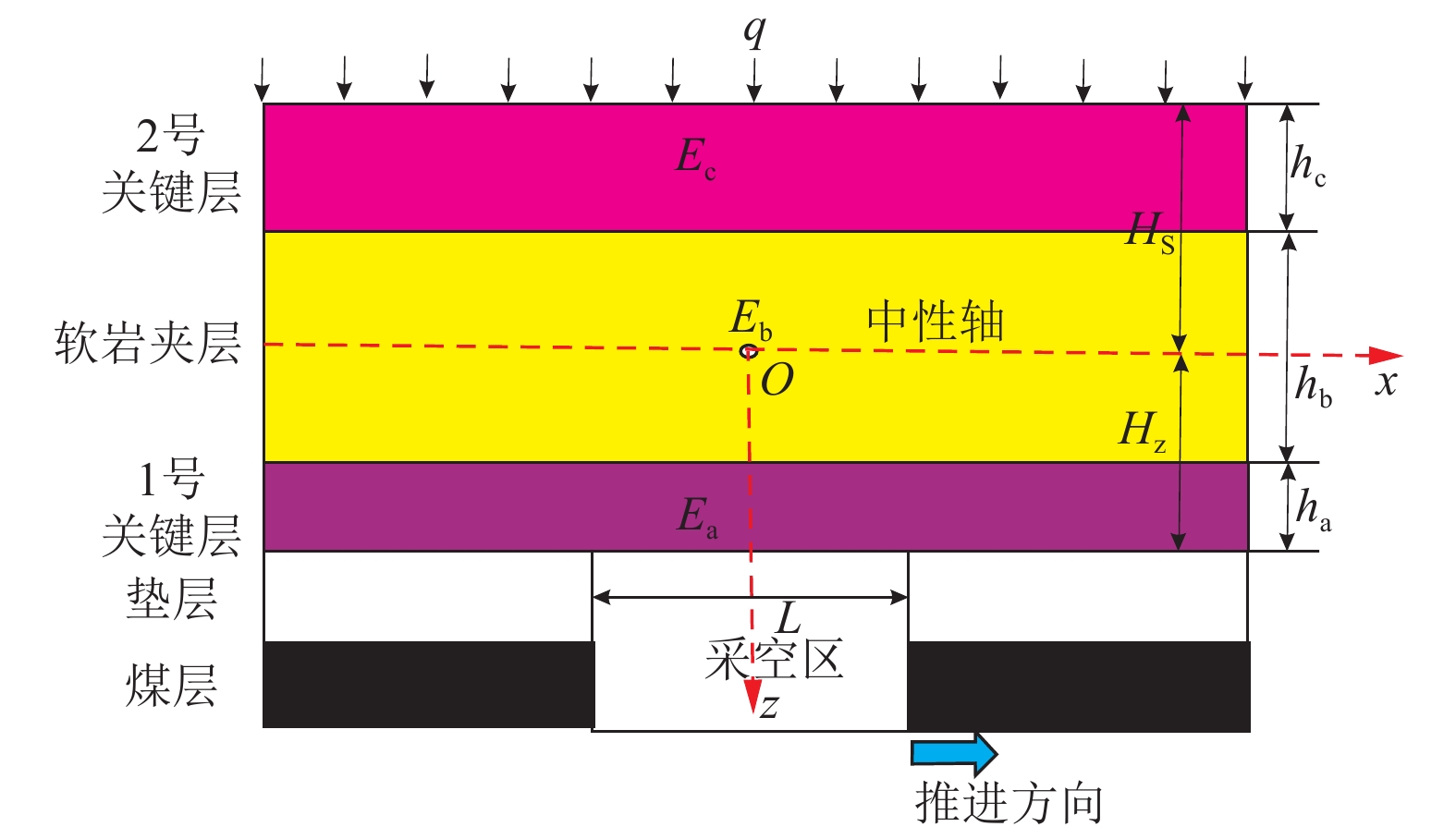
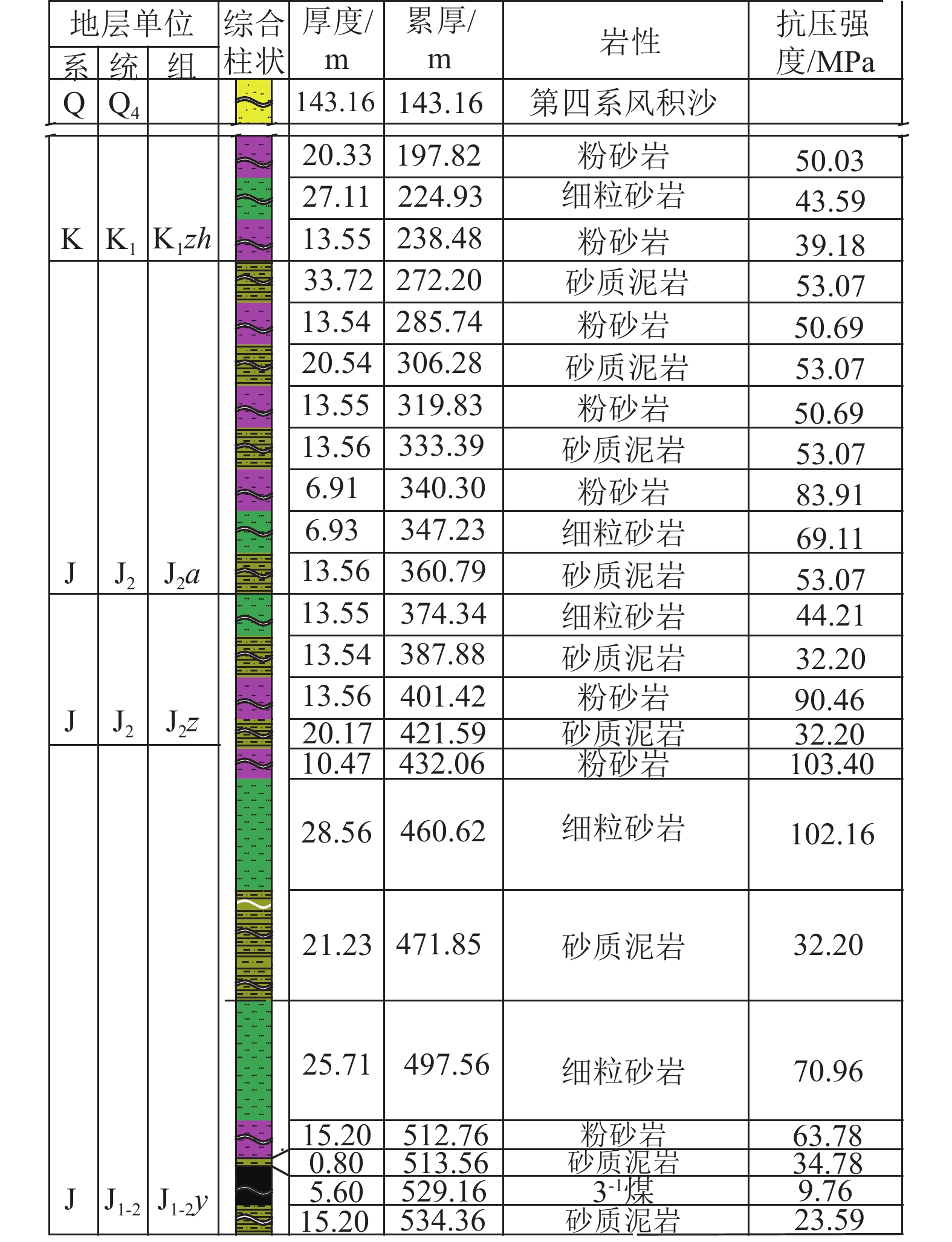
表 1 模型岩层力学参数
Table 1 Mechanical parameters of rock layers in the model
岩性 编号 层位 正应力/MPa 内摩擦角/(°) 黏聚力/MPa 计算剪切强度/MPa 泊松比 抗拉强度/MPa 弹性模量/GPa 砂岩 1-1 下位关键层顶板 14.28 30.50 5.40 13.81 0.26 5.62 7.38 1-2 下位关键层顶板 14.28 32.00 6.10 15.02 0.25 5.74 9.26 1-3 下位关键层顶板 14.28 30.87 5.70 14.24 0.23 6.02 8.58 平均 14.28 31.12 5.73 14.35 0.25 5.79 8.41 泥岩 2-1 软岩夹层 14.05 24.96 3.78 10.32 0.28 2.85 2.82 2-2 软岩夹层 14.05 28.26 2.95 10.50 0.32 2.71 2.65 2-3 软岩夹层 14.05 24.60 3.25 9.68 0.31 1.98 2.78 平均 14.05 25.94 3.33 10.16 0.30 2.51 2.75 砂岩 3-1 上位关键层顶板 13.38 32.20 6.16 14.59 0.24 6.34 11.02 3-2 上位关键层顶板 13.38 36.26 5.98 15.79 0.21 5.89 10.58 3-3 上位关键层顶板 13.38 36.11 7.34 17.10 0.25 7.02 10.23 平均 13.38 34.85 6.49 15.81 0.23 6.42 10.61 
下载: 导出CSV
表 2 模型相似材料配比
Table 2 Ratios of similar materials in the model
序号 岩石
名称密度/
(kg·m−3)体积
模量/GPa剪切模量/
GPa抗拉
强度/MPa黏聚力/
MPa1 砂质泥岩 2 400 15.3 10.5 2.0 1.20 2 3-1煤层 1 400 5.4 3.6 0.3 0.78 3 粉砂岩 2 400 18.5 10.2 2.2 1.55 4 细粒砂岩 2 500 17.0 9.5 2.3 1.32 5 砂质泥岩 2 400 15.3 10.5 2.0 1.20 6 粉砂岩 2 400 18.5 10.2 2.2 1.55 7 细粒砂岩 2 500 17.0 9.5 2.3 1.32 8 粉砂岩 2 400 18.5 10.2 2.2 1.55 9 砂质泥岩 2 400 15.3 10.5 2.0 1.20 10 粉砂岩 2 400 18.5 10.2 2.2 1.55 11 砂质泥岩 2400 15.3 10.5 2.0 1.20 12 细粒砂岩 2500 17.0 9.5 2.3 1.32 13 砂质泥岩 2400 15.3 10.5 2.0 1.20 14 细粒砂岩 2500 17.0 9.5 2.3 1.32 15 粉砂岩 2400 18.5 10.2 2.2 1.55 16 砂质泥岩 2400 15.3 10.5 2.0 1.20 17 粉砂岩 2400 18.5 10.2 2.2 1.55
下载: 导出CSV
-
[1] 王家臣. 基于采动岩层控制的煤炭科学开采[J]. 采矿与岩层控制工程学报,2019,24(2):34−41. WANG Jiachen. Sustainable coal mining based on mining ground control[J]. Journal of Mining and Strata Control Engineering,2019,24(2):34−41.
[2] 王兆会,唐岳松,李猛,等. 深埋薄基岩采场覆岩冒落拱与拱脚高耸岩梁复合承载结构形成机理与应用[J]. 煤炭学报,2023,48(2):563−575. WANG Zhaohui,TANG Yuesong,LI Meng,et al. Development and application of overburden structure composed of caving arch and towering roof beam in deep longwall panel with thin bedrock[J]. Journal of China Coal Society,2023,48(2):563−575.
[3] 钱鸣高,许家林. 煤炭开采与岩层运动[J]. 煤炭学报,2019,44(4):973−984. QIAN Minggao,XU Jialin. Behaviors of strata movement in coal mining[J]. Journal of China Coal Society,2019,44(4):973−984.
[4] 柴敬,雷武林,杜文刚,等. 分布式光纤监测的采场巨厚复合关键层变形试验研究[J]. 煤炭学报,2020,45(1):44−53. CHAI Jing,LEI Wulin,DU Wengang,et al. Deformation of huge thick compound key layer in stope based on distributed optical fiber sensing monitoring[J]. Journal of China Coal Society,2020,45(1):44−53.
[5] DU Wenfeng,PENG Suping,ZHU Guowei,et al. Time-lapse geophysical technology-based study on overburden strata changes induced by modern coal mining[J]. International Journal of Coal Science & Technology,2014,1(2):184−191.
[6] 茅献彪,缪协兴,钱鸣高. 采动覆岩中复合关键层的断裂跨距计算[J]. 岩土力学,1999,20(2):1−4. DOI: 10.3969/j.issn.1000-7598.1999.02.001 MAO Xianbiao,MIAO Xiexing,QIAN Minggao. Calculation for fracture span of conpound key strata in mining rocks[J]. Rock and Soil Mechanics,1999,20(2):1−4. DOI: 10.3969/j.issn.1000-7598.1999.02.001
[7] 缪协兴,茅献彪,孙振武,等. 采场覆岩中复合关键层的形成条件与判别方法[J]. 中国矿业大学学报,2005,34(5):547−550. DOI: 10.3321/j.issn:1000-1964.2005.05.002 MIAO Xiexing,MAO Xianbiao,SUN Zhenwu,et al. Formation conditions of compound key strata in mining overlayer strata and its discriminance[J]. Journal of China University of Mining & Technology,2005,34(5):547−550. DOI: 10.3321/j.issn:1000-1964.2005.05.002
[8] 许家林,鞠金峰. 特大采高综采面关键层结构形态及其对矿压显现的影响[J]. 岩石力学与工程学报,2011,30(8):1547−1556. XU Jialin,JU Jinfeng. Structural morphology of key stratum and its influence on strata behaviors in fully-mechanized face with super-large mining height[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(8):1547−1556.
[9] 闫少宏,尹希文,许红杰,等. 大采高综采顶板短悬臂梁−铰接岩梁结构与支架工作阻力的确定[J]. 煤炭学报,2011,36(11):1816−1820. YAN Shaohong,YIN Xiwen,XU Hongjie,et al. Roof structure of short cantilever-articulated rock beam and calculation of support resistance in full-mechanized face with large mining height[J]. Journal of China Coal Society,2011,36(11):1816−1820.
[10] 张培鹏,蒋力帅,刘绪峰,等. 高位硬厚岩层采动覆岩结构演化特征及致灾规律[J]. 采矿与安全工程学报,2017,34(5):852−860. ZHANG Peipeng,JIANG Lishuai,LIU Xufeng,et al. Mining-induced overlying strata structure evolution characteristics and disaster-triggering under high level hard thick strata[J]. Journal of Mining & Safety Engineering,2017,34(5):852−860.
[11] 潘红宇,李树刚,张涛伟,等. Winkler地基上复合关键层模型及其力学特性[J]. 中南大学学报(自然科学版),2012,43(10):4050−4056. PAN Hongyu,LI Shugang,ZHANG Taowei,et al. Composite key stratum module of Winkler foundation and its mechanical properties[J]. Journal of Central South University (Science and Technology),2012,43(10):4050−4056.
[12] ZHU Cheng,YUAN Yong,YUAN Chaofeng,et al. Study on the structural forms of the key strata in the overburden of a stope during periodic weighting and the reasonable working resistance of the support[J]. Energy Science & Engineering,2020,8(7):2599−2620.
[13] 于斌,杨敬轩,刘长友,等. 大空间采场覆岩结构特征及其矿压作用机理[J]. 煤炭学报,2019,44(11):3295−3307. YU Bin,YANG Jingxuan,LIU Changyou,et al. Overburden structure and mechanism of rock pressure in large space stope[J]. Journal of China Coal Society,2019,44(11):3295−3307.
[14] 王海洋. 复合坚硬顶板变形破断特征及对矿压显现的影响规律[D]. 重庆:重庆大学,2017. WANG Haiyang. Deformation and breaking characteristics of compound hard roof and its influence on pressure behavior[D]. Chongqing:Chongqing University,2017.
[15] 杨俊哲,郑凯歌,王振荣,等. 坚硬顶板动力灾害超前弱化治理技术[J]. 煤炭学报,2020,45(10):3371−3379. YANG Junzhe,ZHENG Kaige,WANG Zhenrong,et al. Technology of weakening and danger-breaking dynamic disasters by hard roof[J]. Journal of China Coal Society,2020,45(10):3371−3379.
[16] 郑凯歌,杨俊哲,李彬刚,等. 基于垮落充填的坚硬顶板分段压裂弱化解危技术[J]. 煤田地质与勘探,2021,49(5):77−87. ZHENG Kaige,YANG Junzhe,LI Bingang,et al. Collapse filling-based technology of weakening and danger-solving by staged fracturing in hard roof[J]. Coal Geology & Exploration,2021,49(5):77−87.
[17] 高瑞. 远场坚硬岩层破断失稳的矿压作用机理及地面压裂控制研究[D]. 徐州:中国矿业大学,2018. GAO Rui. The mechanism of ground pressure induced by the breakage of far-field hard strata and the control technology of ground fracturing[D]. Xuzhou:China University of Mining and Technology,2018.
[18] 郑凯歌,袁亮,杨森,等. 基于分区弱化的复合坚硬顶板冲击地压分段压裂区域防治研究[J]. 采矿与安全工程学报,2023,40(2):322−333. ZHENG Kaige,YUAN Liang,YANG Sen,et al. Study on prevention and control of rock burst staged fracturing area of composite hard roof based on zoning weakening[J]. Journal of Mining & Safety Engineering,2023,40(2):322−333.
[19] 吴学明,马小辉,吕大钊,等. 彬长矿区“井上下” 立体防治冲击地压新模式[J]. 煤田地质与勘探,2023,51(3):19−26. WU Xueming,MA Xiaohui,LYU Dazhao,et al. A new model of surface and underground integrated three-dimensional prevention and control of rock burst in Binchang Mining Area[J]. Coal Geology & Exploration,2023,51(3):19−26.
[20] 张有乾. 考虑层间剪切特性复合顶板失稳机理及控制[D]. 徐州:中国矿业大学,2015. ZHANG Youqian. Instability and control mechanism of layered compound roof in consideration of shear behavior of bedding plane[D]. Xuzhou:China University of Mining and Technology,2015.
[21] LI Zhu,XU Jialin,YU Shengchao,et al. Mechanism and prevention of a chock support failure in the longwall top-coal caving faces:A case study in Datong Coalfield,China[J]. Energies,2018,11(2):288. DOI: 10.3390/en11020288
[22] WANG Feng,XU Jialin,XIE Jianlin,et al. Mechanisms influencing the lateral roof roadway deformation by mining-induced fault population activation:A case study[J]. International Journal of Oil,Gas and Coal Technology,2016,11(4):411. DOI: 10.1504/IJOGCT.2016.075115
计量
- 文章访问数: 166
- HTML全文浏览量: 27
- PDF下载量: 48
