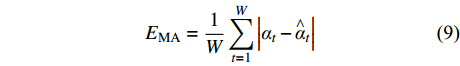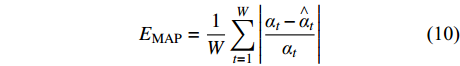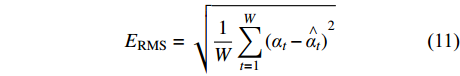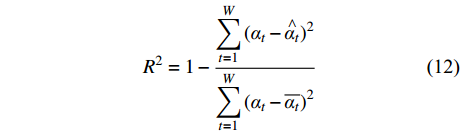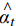Prediction method and application of gas emission from mining workface based on STL-EEMD-GA-SVR
-
摘要:
瓦斯涌出量准确预测可为矿井通风及瓦斯灾害防治措施提供重要依据。为提高采煤工作面瓦斯涌出量预测精度，根据陕西黄陵某矿采煤工作面绝对瓦斯涌出量监测数据，应用基于局部加权回归的周期趋势分解(Seasonal-Trend decomposition procedure based on Loess, STL)，将监测数据分解成趋势项、周期项和不规则波动项；利用集成经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)，将不规则波动项分解得到不同特征尺度的IMFs(Intrinsic Mode Functions, IMFs)分量以及残差余量；通过遗传算法(Genetic Algorithms, GA)参数寻优后的支持向量回归机(Support Vector Regression, SVR)，对各项分解数据进行预测；叠加各分量模型预测结果，得到最终瓦斯涌出量预测结果。结果表明：在预测集为247、147和70组3种情景下，对比分析了STL-EEMD-GA-SVR模型(简称SEGS)、EEMD-GA-SVR模型、GA-SVR模型和高斯过程回归(Gaussian Process Regression, GPR)模型的评价指标精度，其中，SEGS模型最优，拟合度R2分别为0.81、0.92、0.99，峰值点平均相对误差最低，分别为3.15%、2.33%、1.04%。所构建的SEGS模型可以准确预测采煤工作面的瓦斯涌出量。
Abstract:Accurate prediction of gas emission can provide important basis for mine ventilation and the prevention and measures of gas disasters. In order to improve the prediction accuracy of gas emission in the mining workface, the monitoring data of gas emission were decomposed into the trend term, periodic term and irregular fluctuation term by the Seasonal-Trend decomposition procedure based on Loess (STL) based on the monitoring data of gas emission from the mining workface of Huangling Mine in Shaanxi. Besides, the irregular fluctuation term was further broken down into the Intrinsic Mode Functions (IMFs) components with different characteristics and the residual margins by the Ensemble Empirical Mode Decomposition (EEMD). Then, each decomposed data was predicted by the Support Vector Regression (SVR) through parameter optimization by Genetic Algorithms (GA). Moreover, the prediction result of each component model was superposed to obtain the final prediction result of gas emission. In addition, the evaluation indicators for precision of STL-EEMD-GA-SVR model (hereinafter referred to as SEGS), EEMD-GA-SVR model, GA-SVR model and Gaussian Process Regression (GPR) model were analyzed comparatively in the 3 scenarios with 247, 147 and 70 groups of prediction set. According to the results, SEGS model is the best, of which the fitting degree R2 was 0.81, 0.92 and 0.99 respectively, and the average relative error at the peak point was 3.15%, 2.33% and 1.04% respectively. In general, the constructed SEGS model could accurately predict the gas emission of mining workface.
-
瓦斯是影响矿井安全生产的主要因素之一，随着煤炭开采深度及强度增大，矿井瓦斯涌出量也逐渐增加[1-3]。瓦斯涌出量的准确预测可为制定瓦斯防治措施提供重要依据[4-5]。针对瓦斯涌出量预测，传统的矿山统计法、分源预测法、瓦斯地质统计法和类比法等尚未考虑瓦斯涌出是一个动态非线性系统[6-8]。
为解决该问题，基于机器学习算法、数据挖掘等技术的瓦斯涌出量动态预测方法得到了快速发展。此类预测方法主要分为考虑多参数指标和时间序列两类。根据影响瓦斯涌出量诸多参数建立起的多参数指标预测方法[9-15]，大多数煤矿只能提供瓦斯涌出量历史数据，对于影响瓦斯涌出量的煤层厚度、邻近层瓦斯含量等相关数据难以详尽[16]，加之对影响参数取舍不同，使得建立的预测模型与实际情况仍有一定差距。因此，诸多学者开展了瓦斯涌出量时间序列的预测研究分析。陶云奇等[17]将改进的灰色模型与马尔柯夫模型结合建立了中岭煤矿瓦斯涌出量预测模型；高莉等[18]利用混沌时间序列特性构建了小波−径向基神经网络预测模型；单亚锋[19]、程健[20]等通过对时间序列进行相空间重构构建了瓦斯涌出的混沌预测模型；在以上研究基础上引入信号分解中的经验模态分解方法，预先对瓦斯涌出量时序数据进行分解处理，而后运用支持向量机、粒子群−支持向量机、果蝇−极限学习机等模型对其预测，进一步提升了瓦斯涌出量预测精度[8,21-24]。
但基于经验模态分解构建的预测模型，分解过程中若瓦斯涌出量时序数据极值点分布不均匀会出现模态混叠、端点效应等问题，进而影响预测精度；同时，瓦斯涌出量时序数据作为众多影响因素的综合表征，需进一步从时序数据本身来挖掘其潜在规律。因此，笔者以陕西黄陵某矿采煤工作面347个日监测绝对瓦斯涌出量数据为例，应用基于局部加权回归的周期趋势分解(Seasonal-Trend decomposition procedure based on Loess，STL)和集成经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)进行数据分解，通过遗传算法(Genetic Algorithms，GA)参数寻优后的支持向量回归机(Support Vector Regression, SVR)构建了可以挖掘数据本身潜在规律的STL-EEMD-GA-SVR预测模型(简称SEGS)，并与EEMD-GA-SVR、GA-SVR和高斯过程回归(Gaussian Process Regression, GPR)模型预测效果进行对比分析，以期为瓦斯涌出量的精准预测提供有效方法。
1 瓦斯涌出量预测模型建立
1.1 基于局部加权回归的周期趋势分解(STL)
时序数据通常可被分解为趋势项、周期项和不规则波动项3部分[25]。工作面日产量、日推进度、煤层和围岩瓦斯含量、地面大气压、地质构造、开采深度及风量等都会对瓦斯涌出量产生影响[26]，其中开采深度、煤层和围岩瓦斯含量等对工作面瓦斯涌出量产生趋势性影响；日产量、日推进度及风量等对工作面瓦斯涌出量产生周期性影响；地质构造变化、大气压力变化、周期来压等对工作面瓦斯涌出量产生突变影响，这些因素影响都可表征于瓦斯涌出量时序数据。直接使用原始数据，会使数据利用不充分，因此，采用STL分解算法对瓦斯涌出量时序数据进行分解处理[27-28]。
STL包括加法和乘法2种模型[29]，均可将时序数据分解为趋势项Tt、周期项St和不规则波动项It：
$$ {Y_t} = {T_t} + {S_t} + {I_t}{\text{ }} $$ (1) $$ {Y_t} = {T_t} \times {S_t} \times {I_t}{\text{ }} $$ (2) 加法模型适用于相对稳定数据分解，乘法模型适用于趋势项随时间呈现波动变化的数据分解。由于所分析瓦斯涌出量数据整体时序图呈相对稳定状态，因此，选用加法STL时间序列对数据进行分解。
STL关键参数设定：控制趋势效应变化速度的t.window设为13，控制周期效应变化速度的s.window设为“period”，Loess过程使用鲁棒拟合即robust=T。
1.2 集成经验模态分解(EEMD)
瓦斯涌出量时序数据经STL分解后，会得到波动较大、尖峰较多的不规则波动项，此类数据不利于模型训练学习。EEMD方法通过在待分解信号中加入白噪声，可有效抑制经验模态分解混叠现象[30-31]。因此，采用EEMD方法将瓦斯涌出量分解为具有不同特征尺度、尖峰和波动更缓的时序分量数据。EEMD分解原理如下：
(1) 将符合正态分布的白噪声信号加到原始信号中：
$$ X'(t) = X(t) + {\omega _j}(t){\text{ }} $$ (3) 式中：X(t)为原始信号；ωj(t)为白噪声信号；X'(t)为生成的新信号序列；j=1,2,···,M，M为测试次数。
(2) 新信号序列进行EMD分解，得到IMFs(Intrinsic Mode Functions，IMFs)分量：
$$ X'(t) = \sum\limits_{i = 1}^n {{c_{i,j}}(t) + {r_{nj}}(t)} {\text{ }} $$ (4) 式中：n为经EMD分解得到的IMFs分量个数；ci,j(t)为在第j次实验分解中的第i个IMFs分量；rnj(t)为分解得到的残差余量。
(3) 重复上述(1)、(2)步，每次加入不同正态分布的白噪声。
(4) 对各IMFs分量求均值得到最终IMFs分量：
$$ {c_i} = \frac{1}{M}\sum\limits_{j = 1}^M {{c_{i,j}}} $$ (5) EEMD关键参数设定[32]：白噪声标准差设为0.2，白噪声次数设为100。
1.3 GA-SVR模型
SVM在处理小样本、非线性以及高维识别问题上优于其他机器学习算法[33]。SVR则是在SVM基础上通过引入不敏感损失函数实现了回归功能，其具体实现步骤如下：
(1) 假设高维空间的回归函数为：
$$ f(x) = {\text{ω}} \psi (x) + b $$ (6) 式中：ω为权值向量；ψ(x)为非线性映射函数；b为偏置值。
(2) 引入线性不敏感损失函数ε，松弛变量ξi，并求解以下最优化问题：
$$ \left\{\begin{split}&\mathrm{min}\dfrac{1}{2}{\Vert {{ {\textit{ω}}}} \Vert }^{2}+C{\displaystyle \sum _{i=1}^{l}({\xi }_{i}+{\xi }_{i}^{*})}\\ &{\rm{s}}.{\rm{t}}\left\{\begin{split}&{y}_{i}-{ {\textit{ω}}} \psi ({x}_{i})-b\leqslant \varepsilon +{\xi }_{i}^{*}\\ &-{y}_{i}-{ {\textit{ω}}} \psi ({x}_{i})+b\leqslant \varepsilon +{\xi }_{i}^{*}\text{，}\\ &{\xi }_{i}^{*}\geqslant 0，{\xi }_{i}\geqslant 0\end{split}\right.i=1,2,{\cdots},l\end{split}\right. $$ (7) 式中：C为惩罚因子；l为样本集个数。
(3) 对式(7)引入拉格朗日函数，求解得到最终回归函数：
$$ f(x) = \sum\limits_{i = 1}^l {({\alpha _i} - \alpha _i^*)K({x_i},x) + {b^*}} $$ (8) 式中：
$\alpha _i^* $ 、αi为支持向量参数；K(xi,x)为核函数；b*为推导后偏置值。SVR独立预测时，其惩罚因子C和核函数gamma为经验设定，难以保证模型参数最优。GA作为一种具有良好并行性、鲁棒性和全局寻优能力的自适应全局随机搜索优化算法[34]，可有效解决此问题。为此引入GA对SVR关键参数全局寻优，以期建立最优GA-SVR模型。
GA优化SVR关键参数设定：最大遗传迭代次数100，种群大小40，交叉概率0.3，变异概率0.01，代沟0.95；惩罚因子C寻优范围为[0.01,10]，gamma参数寻优范围为[0.01,1000]，交叉验证参数v为3。
1.4 瓦斯涌出量预测模型构建流程
根据以上分析，构建瓦斯涌出量SEGS预测模型流程如图1所示，具体步骤如下。
(1) 数据处理。对缺失、异常样本集数据进行线性插补。
(2) 时序数据分解。STL分解算法将线性插补后数据分解成趋势项、周期项和不规则波动项；EEMD分解算法在此基础上将不规则波动项再次分解，获得各IMFs分量及RES残差余量。
(3) 模型预测。将STL和EEMD分解数据分为训练集、预测集并作归一化处理，利用训练集数据进行模型训练获得最佳GA-SVR模型，运用预测集数据使用GA-SVR模型进行预测，并对预测结果进行反归一化处理，获得各分解分量预测结果。
(4) 分量叠加。将各分量预测结果进行叠加求和，获得最终瓦斯涌出量预测结果。
(5) 模型效果评价。选用平均绝对误差(EMA)、平均绝对百分比误差(EMAP)、均方根误差(ERMS)和判定系数(R2)对预测模型效果评估。其公式如下：
$$ {{E}}_{{\rm{MA}}} = \frac{1}{W}\sum\limits_{t = 1}^W {\left| {{\alpha _t} - {{\mathop \alpha \limits^ \wedge }_t}} \right|} $$ (9) $$ {{E}}_{{\rm{MAP}}} = \frac{1}{W}\sum\limits_{t = 1}^W {\left| {\frac{{{\alpha _t} - {{\mathop \alpha \limits^ \wedge }_t}}}{{{\alpha _t}}}} \right|} $$ (10) $$ {{E}}_{{\rm{RMS}}} = \sqrt {\frac{1}{W}\sum\limits_{t = 1}^W {{{({\alpha _t} - \mathop {{\alpha _t}}\limits^ \wedge )}^2}} } $$ (11) $$ {R^2} = 1 - {\frac{{\displaystyle\sum\limits_{t = 1}^W {({\alpha _t} - \mathop {{\alpha _t}}\limits^ \wedge )^2} }}{{{{\displaystyle\sum\limits_{t = 1}^W {({\alpha _t} - \overline {{\alpha _t}} )^2} }}}}} $$ (12) 式中：αt为瓦斯涌出量原始数据，m3/min；
$\mathop {{\alpha _t}}\limits^ \wedge$ 为瓦斯涌出量预测数据，m3/min；t=1, 2, ···,W，d。2 瓦斯涌出量数据处理
2.1 数据获取及检测
以陕西黄陵某矿采煤工作面为研究对象。该工作面主采2号煤层，煤厚平均3.0 m，煤层倾角平均2°，瓦斯含量0.61~7.70 m3/t，采用本煤层钻孔、高位钻孔和上隅角埋管等方法抽采工作面瓦斯。收集该工作面2020-05-16—2021-04-27瓦斯风排量和抽采量数据，得到绝对瓦斯涌出量数据，见表1。
表 1 瓦斯涌出量数据Table 1. Gas emission data序号 时间 瓦斯风排量/ (m3·min−1) 瓦斯抽采量/
(m3·min−1)绝对瓦斯涌出量/
(m3·min−1)1 2020-05-16 7.37 29.96 37.33 2 2020-05-17 5.94 30.92 36.86 3 2020-05-18 7.78 31.00 38.78 4 2020-05-19 6.14 31.62 37.76 5 2020-05-20 6.55 31.96 38.52 $ \vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ 343 2021-04-23 4.54 41.98 46.52 344 2021-04-24 5.45 41.45 46.89 345 2021-04-25 5.63 41.83 47.46 346 2021-04-26 5.45 42.09 47.53 347 2021-04-27 5.45 NA 5.45 注：NA表示此处为缺失值。 为保证模型预测精度，构建模型之前需对收集数据进行异常值及缺失值检测。将±1.5IQR(IQR表示四分位距)之外数据点作为异常值，以此为标准绘制如图2所示箱线图。由图中可知，所搜集数据均在正常区间范围。针对缺失值通过语句shuju[!complete.cases (shuju),]获得，见表2共6组。
表 2 瓦斯涌出量缺失数据Table 2. Missing data of gas emission序号 时间 瓦斯风排
量/(m3·min−1)瓦斯抽采
量/
(m3·min−1)绝对瓦斯涌出量/
(m3·min−1)200 2020-12-01 6.64 NA 6.64 209 2020-12-10 5.91 NA 5.91 241 2021-01-11 9.19 NA 9.19 275 2021-02-14 4.33 NA 4.33 281 2021-02-20 6.57 NA 6.57 347 2021-04-27 5.45 NA 5.45 注：NA表示此处为缺失值。 2.2 数据插补
时间序列模型一般需保证时序数据的完整性，若直接剔除缺失值，容易导致数据周期错位。为保证数据完整性，需作数据插补处理。目前常用插补方法有均值插补、线性插补、多重插补和EM插补[35]等。为优选出所收集数据的最佳填补方法，本文将原始数据中不包含缺失值的涌出量数据(2020-05-16—2020-08-23)作为试验完整样本，在随机缺失情景[36]利用均值插补、线性插补和多重插补进行插补实验，并将插补结果与实际值进行均方误差[37]比较，以此评估各方法插补精度。各插补方法均方误差见表3。
表 3 随机缺失插补误差对比Table 3. Comparison of interpolation error for random missing values不同插补方法下的均方误差 缺失率/% 二重
插补三重
插补四重
插补五重插补 均值插补 线性插补 5 4.29 21.26 8.40 7.24 2.31 0.12 10 12.77 25.45 21.50 12.71 14.38 0.13 15 20.51 14.46 10.43 13.88 7.04 0.37 20 13.46 9.21 17.11 24.98 11.10 0.24 25 14.87 16.52 17.28 14.04 13.26 0.43 30 15.05 11.87 9.52 14.64 9.06 0.39 由表3可知，线性插补的插补精度最高。为此，本文选用线性插补方法插补缺失值，插补结果见表4。
表 4 线性插补填补数据Table 4. Linear interpolation fill data values序号 时间 瓦斯风排
量/
(m3·min−1)瓦斯抽采
量/
(m3·min−1)绝对瓦斯涌出
量/
(m3·min−1)200 2020-12-01 6.64 45.87 52.51 209 2020-12-10 5.91 45.65 51.56 241 2021-01-11 9.19 41.45 50.64 275 2021-02-14 4.33 45.85 50.18 281 2021-02-20 6.57 41.75 48.32 347 2021-04-27 5.45 43.14 48.59 3 瓦斯涌出量预测及效果检验
3.1 瓦斯涌出量数据的时序分解
经线性插补后的数据自2020-05-16—2021-04-27共计347组。针对瓦斯涌出量时序数据作STL分解，经分解得到趋势项、周期项和不规则波动项，如图3所示。
![]()
图 3 STL分解后采煤工作面瓦斯涌出量Figure 3. Gas emission data of mining workface after STL decomposition由图3可知，趋势项和周期项可以提取出大部分有效信息：趋势项反映了瓦斯涌出量在搜集时间段内的整体变化特征，通过此分解序列可知该工作面瓦斯涌出量初期较小，之后瓦斯涌出量在50~60 m3/min波动，具有一定的线性特征；周期项符合待分析时间序列平稳性的要求，规律性强，有利于GA-SVR模型的训练学习。不规则波动项主要为一些未被趋势或周期效应解释的变化，剩余信息较少，从分解图中可知其具有较强的波动性和随机性，波动和尖峰较多，不利于构建时间序列预测模型。
为降低不规则波动项的波动和尖峰影响采用EEMD分解算法对其进行平稳化处理，结果如图4所示。
由图4可知，不规则波动项经EEMD分解得到7个IMFs分量和1个RES残差余量。分解后的各分量数据相较于最初数据，其振动周期逐渐增加、波动趋势逐渐减缓，平稳性明显优化。
为评估EEMD分解后的数据是否会造成不规则波动项中突变信息的丢失。将不规则波动项与EEMD分解分量叠加值作对比(图5、表5)。
![]()
图 5 不规则波动项与EEMD分解分量叠加值对比Figure 5. Comparison of irregular fluctuation term with superposed value of decomposition components by EEMD表 5 分解损失量Table 5. Decomposition loss序号 时间 不规则波动
项/(m3·min−1)分解分量叠加
值/(m3·min−1)分解损失量/
(m3·min−1)1 2020-05-16 −1.440 4 −1.423 1 −0.017 3 2 2020-05-17 −1.151 0 −1.189 6 0.038 6 3 2020-05-18 1.073 0 1.054 0 0.019 0 4 2020-05-19 0.360 0 0.337 9 0.022 1 5 2020-05-20 1.922 6 1.903 0 0.019 5 $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ 343 2021-04-23 −0.693 5 −0.664 0 −0.029 5 344 2021-04-24 −0.313 8 −0.305 1 −0.008 6 345 2021-04-25 0.023 9 0.081 1 −0.057 2 346 2021-04-26 −0.221 4 −0.236 6 0.015 2 347 2021-04-27 0.649 1 0.634 8 0.014 3 注：为避免保留2位小数出现多处零值，此处保留小数点后4位。其中分解损失量为不规则波动项与分解分量叠加值的差值。 由图5、表5可知，经EEMD分解分量叠加后的数据曲线与不规则波动项曲线呈重合态；数据分解损失量较小，平均分解损失量为0.000 4 m3/min。EEMD分解分量在保留原始数据信息的情况下，降低了原始数据复杂度，提升了平稳性，更有助于预测模型学习其特征进而提高预测精度。
3.2 瓦斯涌出量预测
为验证分解序列预测效果，将分解数据按一定比例分为训练集与预测集，共划分3种情景(情景一：训练集100组，预测集247组；情景二：训练集200组，预测集147组；情景三：训练集277组，预测集70组)。
运用训练集数据实现GA对各分量SVR模型超参数寻优，其寻优值见表6。以此确定各分量最佳模型参数，完成GA-SVR预测模型的构建。
表 6 GA各分量SVR模型超参数寻优值Table 6. Optimal value of hyperparameters for each SVR component model of GA分解分量 情景一寻优值 情景二寻优值 情景三寻优值 bestc bestg bestc bestg bestc bestg IMF1 9.78 0.03 5.23 0.56 9.63 0.01 IMF2 9.61 0.32 8.31 0.02 9.47 0.02 IMF3 6.44 2.39 3.89 2.25 7.96 0.02 IMF4 3.67 2.10 3.10 4.93 30.1 5.05 IMF5 7.00 0.02 7.76 0.02 9.83 0.01 IMF6 5.89 0.52 6.92 0.53 5.11 4.93 IMF7 7.51 0.02 3.70 4.89 4.39 2.33 RES 7.87 2.34 6.47 0.02 5.22 4.92 趋势项 6.77 0.02 6.63 0.02 3.11 2.41 周期项 6.44 0.58 1.82 2.38 3.86 5.00 注：bestc、bestg分别为GA寻优的最佳惩罚因子C和核函数gamma。 为验证构建模型预测效果，选用预测集数据对采煤工作面未来一段时期的绝对瓦斯涌出量进行预测。
由于文章篇幅所限，论文以情景三为例，对采煤工作面未来70 d的瓦斯涌出量进行预测，其各分量模型预测结果如图6所示，预测结果绝对误差见表7。
![]()
图 6 时序分解各分量模型预测结果Figure 6. Prediction results of each component model in time series decomposition表 7 各分量模型预测绝对误差Table 7. Absolute error of each component model分量预测模型 绝对误差/(m3·min−1) 最小值 最大值 平均值 IMF1 0.000 3 0.412 5 0.051 8 IMF2 0.000 2 0.291 1 0.032 8 IMF3 0.000 4 0.218 8 0.044 2 IMF4 0 0.030 9 0.017 4 IMF5 0 0.016 2 0.007 9 IMF6 0.000 1 0.009 3 0.005 8 IMF7 0.000 1 0.009 4 0.005 2 RES 0 0.001 5 0.000 7 趋势项 0.083 0 3.158 5 0.724 7 周期项 0.001 6 0.014 9 0.010 1 注：为避免保留2位小数出现多处零值，此处保留小数点后4位。 由图6、表7可知，各分量预测模型预测效果较好，其预测曲线与实际曲线重叠度高、拟合优度好，平均绝对误差在0.000 7~0.724 7 m3/min区间变化，维持在较低水平。
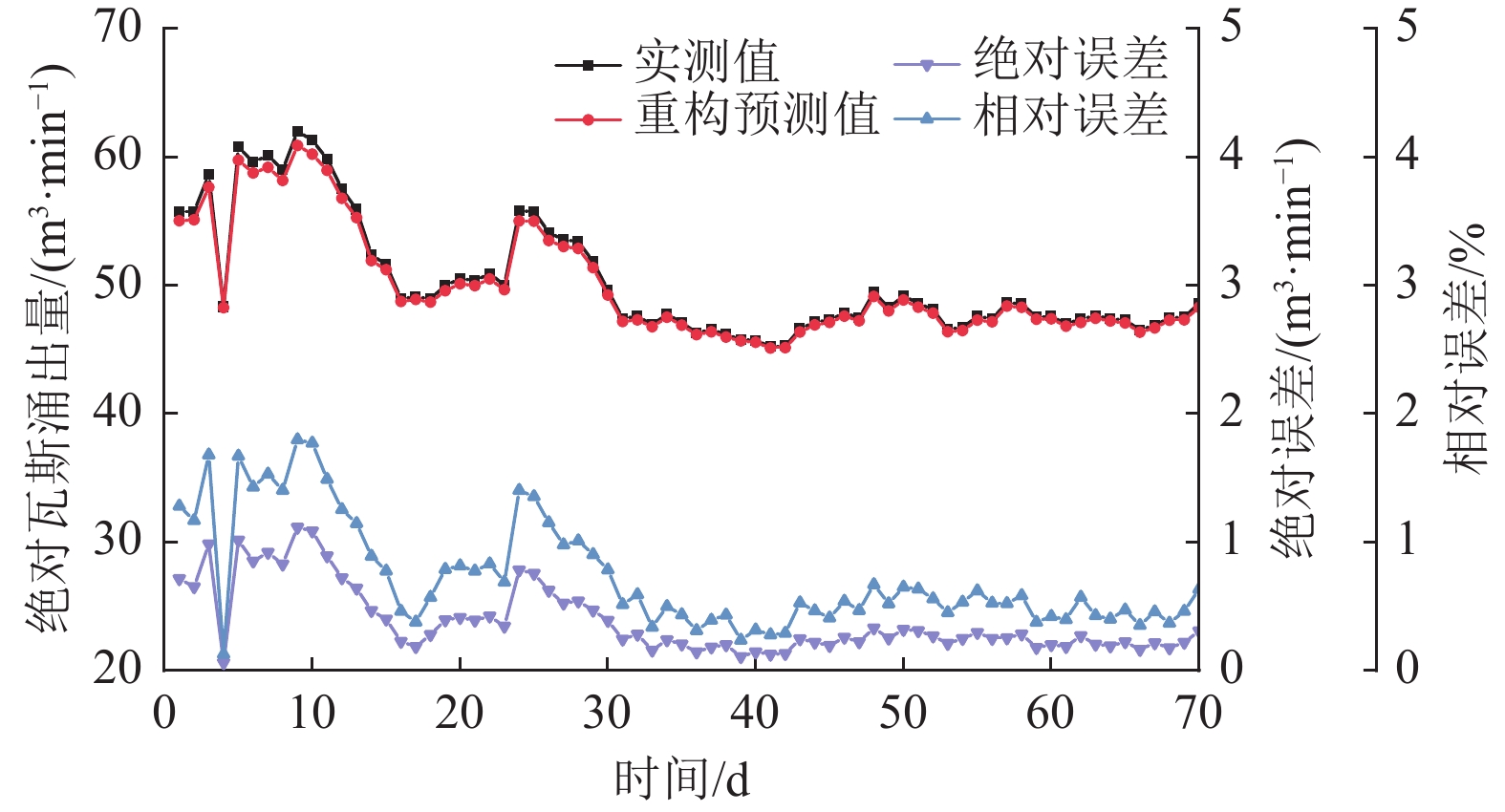
最后，对各分量预测结果进行叠加，重构得到最终绝对瓦斯涌出量预测值(图7)。由图7可知，重构预测值曲线与实测值曲线近乎重合，拟合程度较高；其绝对误差为0.061 5~1.114 9 m3/min，平均0.3852 m3/min；相对误差在0.13%~1.80%，平均0.73%，误差较小。较好地预测了采煤工作面未来70 d的瓦斯涌出量走向趋势，验证了模型具有较高可行性。
3.3 预测模型对比分析
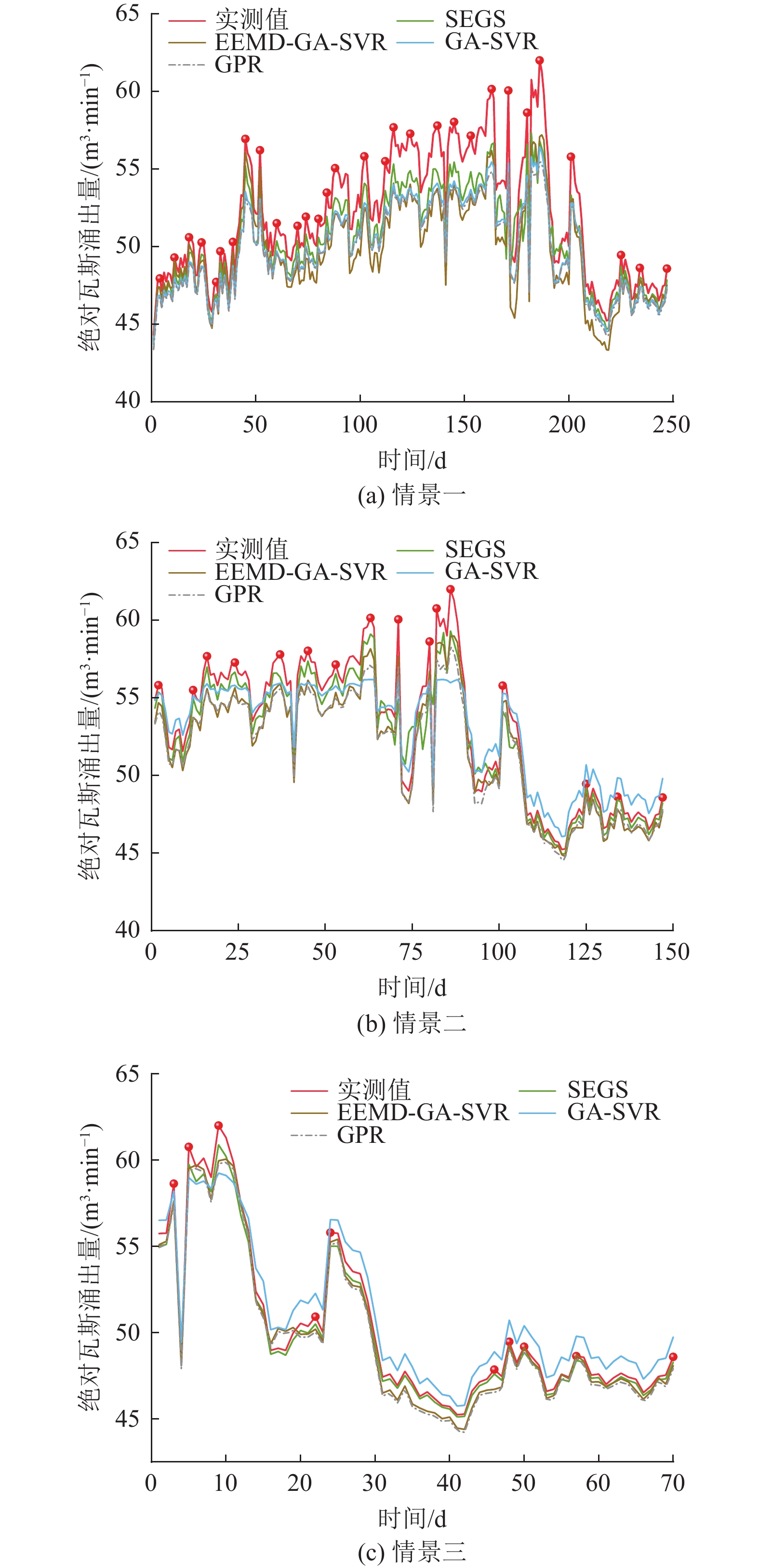
在3种情景下对SEGS、EEMD-GA-SVR、GA-SVR和GPR模型预测结果进行对比(图8、表8)。
![]()
图 8 不同情景下模型预测结果对比注：图中添加符号处表示峰值点。Figure 8. Comparison of model prediction results under different scenarios表 8 各预测模型评价指标对比Table 8. Comparison of evaluation indicators for each prediction model评价指标 SEGS EEMD-GA-SVR GA-SVR GPR 情景一 EMA 1.58 2.32 2.09 2.28 EMAP/% 2.93 4.35 3.88 4.25 ERMS 1.87 2.63 2.33 2.56 R2 0.81 0.67 0.73 0.69 情景二 EMA 0.90 1.29 1.22 1.45 EMAP/% 1.67 2.37 2.25 2.65 ERMS 1.27 1.41 1.54 1.60 R2 0.92 0.91 0.88 0.88 情景三 EMA 0.39 0.59 1.03 0.74 EMAP/% 0.73 1.17 2.05 1.46 ERMS 0.47 0.70 1.10 0.83 R2 0.99 0.98 0.94 0.97 注：EMA、EMAP、ERMS值愈小模型愈优；R2值愈高，模型愈优。 由图8、表8可知，SEGS模型预测效果最优，验证了在EEMD基础上引入STL的必要性。情景一、二、三中SEGS的R2精度分别为0.81、0.92、0.99；其中，情景三中SEGS模型的R2为0.99，优于EEMD-GA-SVR模型的0.98、GA-SVR模型的0.94。
由表8可知，训练集与预测集比例愈大，SEGS模型优势愈明显。情景三中SEGS模型的EMAP值与其他模型最大差值为1.32%；情景三中SEGS模型的指标EMAP低于情景二中SEGS模型的1.67、情景一中的2.93。
为验证瓦斯涌出量时间序列峰值点预测模型的准确性，依据图8所标注峰值点绘制成图9，各模型峰值点预测误差对比见表9。由图9、表9可知：SEGS模型的峰值点预测效果优于对比模型。3种情景下SEGS模型的峰值点相对误差、绝对误差均低于其他模型。
表 9 各模型峰值点预测误差对比Table 9. Comparison of prediction errors at peak points for each model平均值 SEGS EEMD-GA-SVR GA-SVR GPR 情景一 绝对误差/
(m3·min−1)1.77 2.39 2.60 2.85 相对误差/% 3.15 4.29 4.68 5.13 情景二 绝对误差/
(m3·min−1)1.37 1.70 2.16 2.09 相对误差/% 2.33 2.95 3.72 3.62 情景三 绝对误差/
(m3·min−1)0.58 0.75 1.29 0.91 相对误差/% 1.04 1.35 2.40 1.65 综合3种情景、4种模型的对比结果可知，SEGS模型在预测精度及峰值点预测上优于其他3种模型，证明了该预测模型在瓦斯涌出量预测领域的适用性。
4 结 论
a. 提出了采煤工作面瓦斯涌出量预测SEGS模型，基于STL和EEMD将绝对瓦斯涌出量数据分解为趋势项、周期项和不规则波动项(IMFs分量和残差余量)，通过GA参数寻优后的SVR建立了预测模型，该模型降低了数据复杂度，优化了平稳性，提高了预测精度。
b. 通过对比分析多重、均值和线性插补方法精度，确定采用线性方法来进行缺失数据插补，并对6组缺失数据进行处理，保证了数据结构的完整性。
c. 分析了3种不同绝对瓦斯涌出量预测集情景下，SEGS模型、EEMD-GA-SVR模型、GA-SVR模型和GPR模型的预测效果，结果表明SEGS模型整体预测精度最高、峰值点预测误差最小(平均相对误差分别为3.15%、2.33%、1.04%)，证实SEGS模型可有效应用于采煤工作面瓦斯涌出量预测。
d. 受客观条件所限，本文采集的数据样本量有限，今后可针对其他矿井实际情况，进一步验证SEGS模型的普适性；一些与采煤工作面绝对瓦斯涌出量相关的特征(如瓦斯浓度、风量等)尚未考虑，今后在数据允许的条件下可进一步探究。
-
![]()
图 3 STL分解后采煤工作面瓦斯涌出量
Fig. 3 Gas emission data of mining workface after STL decomposition
![]()
图 5 不规则波动项与EEMD分解分量叠加值对比
Fig. 5 Comparison of irregular fluctuation term with superposed value of decomposition components by EEMD
![]()
图 6 时序分解各分量模型预测结果
Fig. 6 Prediction results of each component model in time series decomposition
![]()
图 8 不同情景下模型预测结果对比
注：图中添加符号处表示峰值点。
Fig. 8 Comparison of model prediction results under different scenarios
表 1 瓦斯涌出量数据
Table 1 Gas emission data
序号 时间 瓦斯风排量/ (m3·min−1) 瓦斯抽采量/
(m3·min−1)绝对瓦斯涌出量/
(m3·min−1)1 2020-05-16 7.37 29.96 37.33 2 2020-05-17 5.94 30.92 36.86 3 2020-05-18 7.78 31.00 38.78 4 2020-05-19 6.14 31.62 37.76 5 2020-05-20 6.55 31.96 38.52 $ \vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ 343 2021-04-23 4.54 41.98 46.52 344 2021-04-24 5.45 41.45 46.89 345 2021-04-25 5.63 41.83 47.46 346 2021-04-26 5.45 42.09 47.53 347 2021-04-27 5.45 NA 5.45 注：NA表示此处为缺失值。 
下载: 导出CSV
表 2 瓦斯涌出量缺失数据
Table 2 Missing data of gas emission
序号 时间 瓦斯风排
量/(m3·min−1)瓦斯抽采
量/
(m3·min−1)绝对瓦斯涌出量/
(m3·min−1)200 2020-12-01 6.64 NA 6.64 209 2020-12-10 5.91 NA 5.91 241 2021-01-11 9.19 NA 9.19 275 2021-02-14 4.33 NA 4.33 281 2021-02-20 6.57 NA 6.57 347 2021-04-27 5.45 NA 5.45 注：NA表示此处为缺失值。
下载: 导出CSV
表 3 随机缺失插补误差对比
Table 3 Comparison of interpolation error for random missing values
不同插补方法下的均方误差 缺失率/% 二重
插补三重
插补四重
插补五重插补 均值插补 线性插补 5 4.29 21.26 8.40 7.24 2.31 0.12 10 12.77 25.45 21.50 12.71 14.38 0.13 15 20.51 14.46 10.43 13.88 7.04 0.37 20 13.46 9.21 17.11 24.98 11.10 0.24 25 14.87 16.52 17.28 14.04 13.26 0.43 30 15.05 11.87 9.52 14.64 9.06 0.39
下载: 导出CSV
表 4 线性插补填补数据
Table 4 Linear interpolation fill data values
序号 时间 瓦斯风排
量/
(m3·min−1)瓦斯抽采
量/
(m3·min−1)绝对瓦斯涌出
量/
(m3·min−1)200 2020-12-01 6.64 45.87 52.51 209 2020-12-10 5.91 45.65 51.56 241 2021-01-11 9.19 41.45 50.64 275 2021-02-14 4.33 45.85 50.18 281 2021-02-20 6.57 41.75 48.32 347 2021-04-27 5.45 43.14 48.59
下载: 导出CSV
表 5 分解损失量
Table 5 Decomposition loss
序号 时间 不规则波动
项/(m3·min−1)分解分量叠加
值/(m3·min−1)分解损失量/
(m3·min−1)1 2020-05-16 −1.440 4 −1.423 1 −0.017 3 2 2020-05-17 −1.151 0 −1.189 6 0.038 6 3 2020-05-18 1.073 0 1.054 0 0.019 0 4 2020-05-19 0.360 0 0.337 9 0.022 1 5 2020-05-20 1.922 6 1.903 0 0.019 5 $\vdots $ $\vdots $ $\vdots $ $\vdots $ $\vdots $ 343 2021-04-23 −0.693 5 −0.664 0 −0.029 5 344 2021-04-24 −0.313 8 −0.305 1 −0.008 6 345 2021-04-25 0.023 9 0.081 1 −0.057 2 346 2021-04-26 −0.221 4 −0.236 6 0.015 2 347 2021-04-27 0.649 1 0.634 8 0.014 3 注：为避免保留2位小数出现多处零值，此处保留小数点后4位。其中分解损失量为不规则波动项与分解分量叠加值的差值。
下载: 导出CSV
表 6 GA各分量SVR模型超参数寻优值
Table 6 Optimal value of hyperparameters for each SVR component model of GA
分解分量 情景一寻优值 情景二寻优值 情景三寻优值 bestc bestg bestc bestg bestc bestg IMF1 9.78 0.03 5.23 0.56 9.63 0.01 IMF2 9.61 0.32 8.31 0.02 9.47 0.02 IMF3 6.44 2.39 3.89 2.25 7.96 0.02 IMF4 3.67 2.10 3.10 4.93 30.1 5.05 IMF5 7.00 0.02 7.76 0.02 9.83 0.01 IMF6 5.89 0.52 6.92 0.53 5.11 4.93 IMF7 7.51 0.02 3.70 4.89 4.39 2.33 RES 7.87 2.34 6.47 0.02 5.22 4.92 趋势项 6.77 0.02 6.63 0.02 3.11 2.41 周期项 6.44 0.58 1.82 2.38 3.86 5.00 注：bestc、bestg分别为GA寻优的最佳惩罚因子C和核函数gamma。
下载: 导出CSV
表 7 各分量模型预测绝对误差
Table 7 Absolute error of each component model
分量预测模型 绝对误差/(m3·min−1) 最小值 最大值 平均值 IMF1 0.000 3 0.412 5 0.051 8 IMF2 0.000 2 0.291 1 0.032 8 IMF3 0.000 4 0.218 8 0.044 2 IMF4 0 0.030 9 0.017 4 IMF5 0 0.016 2 0.007 9 IMF6 0.000 1 0.009 3 0.005 8 IMF7 0.000 1 0.009 4 0.005 2 RES 0 0.001 5 0.000 7 趋势项 0.083 0 3.158 5 0.724 7 周期项 0.001 6 0.014 9 0.010 1 注：为避免保留2位小数出现多处零值，此处保留小数点后4位。
下载: 导出CSV
表 8 各预测模型评价指标对比
Table 8 Comparison of evaluation indicators for each prediction model
评价指标 SEGS EEMD-GA-SVR GA-SVR GPR 情景一 EMA 1.58 2.32 2.09 2.28 EMAP/% 2.93 4.35 3.88 4.25 ERMS 1.87 2.63 2.33 2.56 R2 0.81 0.67 0.73 0.69 情景二 EMA 0.90 1.29 1.22 1.45 EMAP/% 1.67 2.37 2.25 2.65 ERMS 1.27 1.41 1.54 1.60 R2 0.92 0.91 0.88 0.88 情景三 EMA 0.39 0.59 1.03 0.74 EMAP/% 0.73 1.17 2.05 1.46 ERMS 0.47 0.70 1.10 0.83 R2 0.99 0.98 0.94 0.97 注：EMA、EMAP、ERMS值愈小模型愈优；R2值愈高，模型愈优。
下载: 导出CSV
表 9 各模型峰值点预测误差对比
Table 9 Comparison of prediction errors at peak points for each model
平均值 SEGS EEMD-GA-SVR GA-SVR GPR 情景一 绝对误差/
(m3·min−1)1.77 2.39 2.60 2.85 相对误差/% 3.15 4.29 4.68 5.13 情景二 绝对误差/
(m3·min−1)1.37 1.70 2.16 2.09 相对误差/% 2.33 2.95 3.72 3.62 情景三 绝对误差/
(m3·min−1)0.58 0.75 1.29 0.91 相对误差/% 1.04 1.35 2.40 1.65
下载: 导出CSV
-
[1] 程远平,周德永,俞启香,等. 保护层卸压瓦斯抽采及涌出规律研究[J]. 采矿与安全工程学报,2006,23(1):12−18. DOI: 10.3969/j.issn.1673-3363.2006.01.003 CHENG Yuanping,ZHOU Deyong,YU Qixiang,et al. Research on extraction and emission laws of gas for pressure–relief in protecting coal seams[J]. Journal of Mining & Safety Engineering,2006,23(1):12−18. DOI: 10.3969/j.issn.1673-3363.2006.01.003
[2] 樊保龙,白春华,李建平. 基于LMD–SVM的采煤工作面瓦斯涌出量预测[J]. 采矿与安全工程学报,2013,30(6):946−952. FAN Baolong,BAI Chunhua,LI Jianping. Forecasting model of coalface gas emission based on LMD–SVM method[J]. Journal of Mining & Safety Engineering,2013,30(6):946−952.
[3] 张超林,王恩元,王奕博,等. 近20年我国煤与瓦斯突出事故时空分布及防控建议[J]. 煤田地质与勘探,2021,49(4):134−141. DOI: 10.3969/j.issn.1001-1986.2021.04.016 ZHANG Chaolin,WANG Enyuan,WANG Yibo,et al. Spatial–temporal distribution of outburst accidents from 2001 to 2020 in China and suggestions for prevention and control[J]. Coal Geology & Exploration,2021,49(4):134−141. DOI: 10.3969/j.issn.1001-1986.2021.04.016
[4] 桂祥友,郁钟铭,孟絮屹. 贵州煤矿瓦斯涌出量灰色预测的应用[J]. 采矿与安全工程学报,2007,24(4):449−452. DOI: 10.3969/j.issn.1673-3363.2007.04.015 GUI Xiangyou,YU Zhongming,MENG Xuyi. Application of grey forecast for coal bed methane emission from coal mines in Guizhou Province[J]. Journal of Mining & Safety Engineering,2007,24(4):449−452. DOI: 10.3969/j.issn.1673-3363.2007.04.015
[5] 付华,于翔,卢万杰. 基于蚁群粒子群混合算法与LS–SVM瓦斯涌出量预测[J]. 传感技术学报,2016,29(3):373−377. DOI: 10.3969/j.issn.1004-1699.2016.03.012 FU Hua,YU Xiang,LU Wanjie. Prediction of gas emission based on hybrid algorithm of Ant Colony Particle Swarm optimization and LS–SVM[J]. Chinese Journal of Sensors and Actuators,2016,29(3):373−377. DOI: 10.3969/j.issn.1004-1699.2016.03.012
[6] 章立清,秦玉金,姜文忠,等. 我国矿井瓦斯涌出量预测方法研究现状及展望[J]. 煤矿安全,2007,38(8):58−60. DOI: 10.3969/j.issn.1003-496X.2007.08.020 ZHANG Liqing,QIN Yujin,JIANG Wenzhong,et al. Research status and prospects of mine gas emission prediction methods in my country[J]. Safety in Coal Mines,2007,38(8):58−60. DOI: 10.3969/j.issn.1003-496X.2007.08.020
[7] 姜文忠,霍中刚,秦玉金. 矿井瓦斯涌出量预测技术[J]. 煤炭科学技术,2008,36(6):1−4. DOI: 10.13199/j.cst.2008.06.6.jiangwzh.018 JIANG Wenzhong,HUO Zhonggang,QIN Yujin. Predicted technology of mine gas emission[J]. Coal Science and Technology,2008,36(6):1−4. DOI: 10.13199/j.cst.2008.06.6.jiangwzh.018
[8] 刘俊娥,安凤平,林大超,等. 采煤工作面瓦斯涌出量的固有模态SVM建模预测[J]. 系统工程理论与实践,2013,33(2):505−511. DOI: 10.3969/j.issn.1000-6788.2013.02.028 LIU Jun’e,AN Fengping,LIN Dachao,et al. Prediction of gas emission from coalface by intrinsic mode SVM modeling[J]. Systems Engineering–Theory & Practice,2013,33(2):505−511. DOI: 10.3969/j.issn.1000-6788.2013.02.028
[9] 付华,谢森,徐耀松,等. 基于MPSO–WLS–SVM的矿井瓦斯涌出量预测模型研究[J]. 中国安全科学学报,2013,23(5):56−61. FU Hua,XIE Sen,XU Yaosong,et al. Study on MPSO−WLS–SVM based mine gas emission prediction model[J]. China Safety Science Journal,2013,23(5):56−61.
[10] 付华,谢森,徐耀松,等. 基于ACC–ENN算法的煤矿瓦斯涌出量动态预测模型研究[J]. 煤炭学报,2014,39(7):1296−1301. FU Hua,XIE Sen,XU Yaosong,et al. Gas emission dynamic prediction model of coal mine based on ACC–ENN algorithm[J]. Journal of China Coal Society,2014,39(7):1296−1301.
[11] 董晓雷,贾进章,白洋,等. 基于SVM耦合遗传算法的回采工作面瓦斯涌出量预测[J]. 安全与环境学报,2016,16(2):114−118. DONG Xiaolei,JIA Jinzhang,BAI Yang,et al. Prediction for gas–gushing amount from the working face of stope based on the SVM coupling genetic algorithm[J]. Journal of Safety and Environment,2016,16(2):114−118.
[12] 温廷新,孙雪,孔祥博,等. 基于PSOBP–AdaBoost模型的瓦斯涌出量分源预测研究[J]. 中国安全科学学报,2016,26(5):94−98. WEN Tingxin,SUN Xue,KONG Xiangbo,et al. Research on prediction of gas emission quantity with sub sources basing on PSOBP–AdaBoost[J]. China Safety Science Journal,2016,26(5):94−98.
[13] 周鑫隆,章光,吕辰,等. 深部煤层瓦斯含量的差值GM–RBF预测模型及其应用[J]. 安全与环境学报,2017,17(6):2050−2055. ZHOU Xinlong,ZHANG Guang,LYU Chen,et al. A grey model for predicting the gas content in the deep coal seam and its application via the neural network of the difference radial basis function[J]. Journal of Safety and Environment,2017,17(6):2050−2055.
[14] 林海飞,高帆,严敏,等. 煤层瓦斯含量PSO–BP神经网络预测模型及其应用[J]. 中国安全科学学报,2020,30(9):80−87. LIN Haifei,GAO Fan,YAN Min,et al. Study on PSO–BP neural network prediction method of coal seam gas content and its application[J]. China Safety Science Journal,2020,30(9):80−87.
[15] 马文涛. 基于WT与GALSSVM的瓦斯涌出量预测[J]. 采矿与安全工程学报,2009,26(4):524−528. DOI: 10.3969/j.issn.1673-3363.2009.04.028 MA Wentao. Gas emission forecast based on WT and GALSSVM[J]. Journal of Mining & Safety Engineering,2009,26(4):524−528. DOI: 10.3969/j.issn.1673-3363.2009.04.028
[16] 任海峰,严由吉,吴青海. 基于SAPSO–ELM的瓦斯涌出量分源预测及应用[J]. 煤田地质与勘探,2021,49(2):102−109. DOI: 10.3969/j.issn.1001-1986.2021.02.013 REN Haifeng,YAN Youji,WU Qinghai. Different–source prediction of gas emission based on SAPSO–ELM and its application[J]. Coal Geology & Exploration,2021,49(2):102−109. DOI: 10.3969/j.issn.1001-1986.2021.02.013
[17] 陶云奇,许江,李树春. 改进的灰色马尔柯夫模型预测采煤工作面瓦斯涌出量[J]. 煤炭学报,2007,32(4):391−395. DOI: 10.3321/j.issn:0253-9993.2007.04.012 TAO Yunqi,XU Jiang,LI Shuchun. Predict gas emissing quantity of mining coal face with improved grey Markov model[J]. Journal of China Coal Society,2007,32(4):391−395. DOI: 10.3321/j.issn:0253-9993.2007.04.012
[18] 高莉,胡延军,于洪珍. 基于W–RBF的瓦斯时间序列预测方法[J]. 煤炭学报,2008,33(1):67−70. DOI: 10.3321/j.issn:0253-9993.2008.01.015 GAO Li,HU Yanjun,YU Hongzhen. Prediction of gas emission time series based on W–RBF[J]. Journal of China Coal Society,2008,33(1):67−70. DOI: 10.3321/j.issn:0253-9993.2008.01.015
[19] 单亚锋,侯福营,付华,等. 基于改进极端学习机的混沌时间序列瓦斯涌出量预测[J]. 中国安全科学学报,2012,22(12):58−63. SHAN Yafeng,HOU Fuying,FU Hua,et al. Prediction of chaotic time series of gas emission based on improved extreme learning machine[J]. China Safety Science Journal,2012,22(12):58−63.
[20] 程健,白静宜,钱建生,等. 基于混沌时间序列的煤矿瓦斯浓度短期预测[J]. 中国矿业大学学报,2008,37(2):231−235. DOI: 10.3321/j.issn:1000-1964.2008.02.018 CHENG Jian,BAI Jingyi,QIAN Jiansheng,et al. Short–term forecasting method of coal mine gas concentration based on chaotic time series[J]. Journal of China University of Mining & Technology,2008,37(2):231−235. DOI: 10.3321/j.issn:1000-1964.2008.02.018
[21] 施式亮,李润求,罗文柯. 基于EMD–PSO–SVM的煤矿瓦斯涌出量预测方法及应用[J]. 中国安全科学学报,2014,24(7):43−49. SHI Shiliang,LI Runqiu,LUO Wenke. Method for predicting coal mine gas emission based on EMD–PSO–SVM and its application[J]. China Safety Science Journal,2014,24(7):43−49.
[22] 李润求,施式亮,伍爱友,等. 采煤工作面瓦斯涌出预测的EMD–Elman方法及应用[J]. 中国安全科学学报,2014,24(6):51−56. LI Runqiu,SHI Shiliang,WU Aiyou,et al. Research on coal mining workface gas emission prediction method based on EMD–Elman and its application[J]. China Safety Science Journal,2014,24(6):51−56.
[23] 撒占友,刘岩,刘杰. 基于EMD–ARMA的矿井瓦斯涌出量预测[J]. 煤矿安全,2016,47(7):174−176. SA Zhanyou,LIU Yan,LIU Jie. Mine gas emission prediction based on EMD–ARMA model[J]. Safety in Coal Mines,2016,47(7):174−176.
[24] 卢国斌,李晓宇,祖秉辉,等. 基于EMD–MFOA–ELM的瓦斯涌出量时变序列预测研究[J]. 中国安全生产科学技术,2017,13(6):109−114. LU Guobin,LI Xiaoyu,ZU Binghui,et al. Research on time–varying series forecasting of gas emission quantity based on EMD–MFOA−ELM[J]. Journal of Safety Science and Technology,2017,13(6):109−114.
[25] BANAS J,KOZUCH A. The application of time series decomposition for the identification and analysis of fluctuations in timber supply and price:A case study from Poland[J]. Forests,2019,10(11):990. DOI: 10.3390/f10110990
[26] 何清. 工作面瓦斯涌出量预测研究现状及发展趋势[J]. 矿业安全与环保,2016,43(4):98−101. DOI: 10.3969/j.issn.1008-4495.2016.04.026 HE Qing. Present research situation on gas emission prediction of working face and its developing trend[J]. Mining Safety & Environmental Protection,2016,43(4):98−101. DOI: 10.3969/j.issn.1008-4495.2016.04.026
[27] ROJO J,RIVERO R,ROMERO–MORTE J,et al. Modeling pollen time series using seasonal−trend decomposition procedure based on LOESS smoothing[J]. International Journal of Biometeorology,2017,61(2):335−348. DOI: 10.1007/s00484-016-1215-y
[28] XIONG Tao,LI Chongguang,BAO Yukun. Seasonal forecasting of agricultural commodity price using a hybrid STL and ELM method:Evidence from the vegetable market in China[J]. Neurocomputing,2018,275:2831−2844. DOI: 10.1016/j.neucom.2017.11.053
[29] SUN Tianhe,ZHANG Tieyan,TENG Yun,et al. Monthly electricity consumption forecasting method based on X12 and STL decomposition model in an integrated energy system[J]. Mathematical Problems in Engineering,2019,2019:9012543.
[30] 胡爱军,孙敬敬,向玲. 经验模态分解中的模态混叠问题[J]. 振动、测试与诊断,2011,31(4):429−434. DOI: 10.3969/j.issn.1004-6801.2011.04.006 HU Aijun,SUN Jingjing,XIANG Ling. Mode mixing in empirical mode decomposition[J]. Journal of Vibration,Measurement and Diagnosis,2011,31(4):429−434. DOI: 10.3969/j.issn.1004-6801.2011.04.006
[31] 易文华,刘连生,闫雷,等. 基于EMD改进算法的爆破振动信号去噪[J]. 爆炸与冲击,2020,40(9):095201. DOI: 10.11883/bzycj-2019-0471 YI Wenhua,LIU Liansheng,YAN Lei,et al. Vibration signal de–noising based on improved EMD algorithm[J]. Explosion and Shock Waves,2020,40(9):095201. DOI: 10.11883/bzycj-2019-0471
[32] WU Zhaohua,HUANG N E. Ensemble empirical mode decomposition:A noise–assisted data analysis method[J]. Advances in Adaptive Data Analysis,2009,1(1):1−41. DOI: 10.1142/S1793536909000047
[33] 魏博文,柳波,徐富刚,等. 融合PSO–SVM的混凝土拱坝多测点变形监控混合模型[J]. 武汉大学学报(信息科学版),2021,46(11):1−14. WEI Bowen,LIU Bo,XU Fugang,et al. Multi−point hybrid model based on PSO–SVM for concrete arch dam deformation monitoring[J]. Geomatics and Information Science of Wuhan University,2021,46(11):1−14.
[34] 边霞,米良. 遗传算法理论及其应用研究进展[J]. 计算机应用研究,2010,27(7):2425−2429. BIAN Xia,MI Liang. Development on genetic algorithm theory and its applications[J]. Application Research of Computers,2010,27(7):2425−2429.
[35] 邓建新,单路宝,贺德强,等. 缺失数据的处理方法及其发展趋势[J]. 统计与决策,2019,35(23):28−34. DOI: 10.13546/j.cnki.tjyjc.2019.23.005 DENG Jianxin,SHAN Lubao,HE Deqiang,et al. Processing method of missing data and its development tendency[J]. Statistics & Decision,2019,35(23):28−34. DOI: 10.13546/j.cnki.tjyjc.2019.23.005
[36] 赵厚翔,沈晓东,吕林,等. 基于GAN的负荷数据修复及其在EV短期负荷预测中的应用[J]. 电力系统自动化,2021,45(16):143−151. ZHAO Houxiang,SHEN Xiaodong,LYU Lin,et al. Load data restoration based on GAN and its application in short–term load forecasting of EV[J]. Automation of Electric Power Systems,2021,45(16):143−151.
[37] LUO Yonghong, CAI Xiangrui, ZHANG Ying, et al. Multivariate time series imputation with generative adversarial networks[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal, 2018: 1603–1614.
计量
- 文章访问数: 193
- HTML全文浏览量: 11
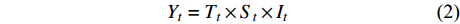
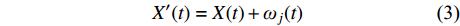
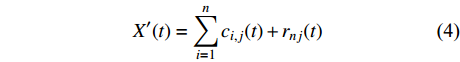
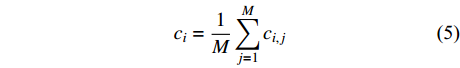
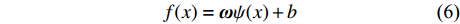
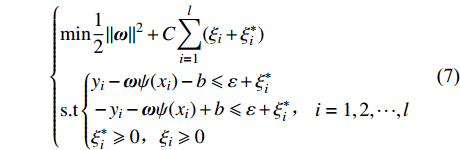
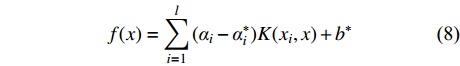
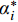
- PDF下载量: 27
